Correspondence to:

Dr. Erhard Bieberich

Institute of Molecular Medicine and Genetics

Medical College of Georgia

1120 15^th Street CB-2803

Augusta, GA 30912
 

Phone: 706-721-9113

Fax: 706-721-8272

E-mail: ebieberich@mail.mcg.edu
 

Keywords: consciousness, Liar paradox, atomism, fractal, quantum mechanics, computation, Halting problem, Turing machine
 

In human consciousness perceptions are distinct or atomistic events despite being perceived by an apparently undivided inner observer. This paper applies both classical (Boolean) and quantum logic to analysis of the Liar paradox which is taken as a typical example of a self-referential negation in the perception space of an undivided observer. The conception of self-referential paradoxes is a unique ability of the human mind still lacking an explanation on the basis of logic. It will be shown that both classical and quantum logics fail to resolve the paradox because of the particle-like (atomistic) nature of physical events in the moments of perception. The atomistic reality is the only one observed in human consciousness even if, as has been claimed by a number of authors, consciousness arises from a quantum mechanical superposition. However, a computational solution of the paradox can be achieved by embedding quantum registers in a fractal space. The truth values, or q-bit eigenstates, of the separate parts of the paradox correspond to sub-spaces of the fractal. Since a fractal contains the whole in each part a self-referential negation emerges as the experienced concept in each sub-space. Fractal quantum computation is realized by a cNOT-operation with percolation of the control q-bits into sub-spaces of a nascent fractal. In other words, atomism cannot cope with a self-referential paradox but quantum logic gates embedded in a fractal structure can cope. Remarkably, it will be shown that a mind operating on these algorithmic principles will not inevitably be limited by Turing's halting theorem. I suggest a physical mechanism that can deal with our experience of self-referential paradox. Because it is also shown that this cannot be achieved by any previously suggested classical or quantum mechanical operation, the newly proposed mechanism provides a better model than others for an important aspect of the structure of our minds.

Three well-known self-referential paradoxes are closely linked with three inter-related impossibility theorems (Chaitin, 1999). The paradoxes are 'I, a Cretan, say that all Cretans are liars' (Epimenides), 'who shaves the barber who shaves everyone who does not shave himself?' (Russell) and 'the first natural number that cannot be named in less than fourteen words' (a thirteen word definition allegedly due to Berry). The theorems that link with them are Gödel's incompleteness, Turing's halting theorem, and Chaitin's information-theoretic formulation of these. In particular, the halting theorem is of importance for a mechanistic description of the human mind. It says that no algorithm exists that can always predict whether a given Turing machine computation will halt (Turing, 1937). Furter, Chaitin has shown that one cannot prove any theorem whose information content exceeds that of its axiom system by more than a fixed number of bits (see Chaitin, 1999, for an accessible account of this). A self-referential negation is fatal for any algorithm since it annihilates its input definitions by its own computational results. Unprovability and self-referential negation are particularly baffling since their conception by the human mind raises the question about whether the mind does in fact operate within an axiomatic system and therefore can be described by an algorithm embodied in a physical mechanism. Hence, any model of consciousness, irrespective of whether it is classical or quantum mechanical, has to be analyzed in the context of these fundamental theorems.
 

Penrose (1989, 1994) has famously argued that human minds are not limited by Goedel incompleteness, hence cannot be Turing machines. If one takes Chaitin's theorem into account, it is easy to see that Penrose's argument cannot amount to a proof. Faced with an 'incomputable' problem, people might subconsciously add 'axioms' to their thought processes until a solution emerged. 'False' solutions could later be winnowed out by Darwinian mechanisms selecting for those solutions best fitted to society or to the world. It is nevertheless possible, however, that Penrose's intuition is valid. I argue here that examination of the Liar paradox, taken as exemplar for self-referential paradoxes, allows one to infer a structure for a type of mind which could escape the limitations of Turing's halting theorem and hence, by implication, Goedel incompleteness. My suggestion, unlike that of Penrose, does not entail the introduction of any new physics and is, I believe, biologically plausible.
 

My model of the type of mind required has three essential components. First, it assumes that much brain activity has a fractal structure. This is uncontentious (see, for example, C.C. King, 1995). Second, it requires that the 'bottom line' of some of the fractal structure be quantum mechanical (see Bieberich, 1999, 2000, for further details). Third, it assumes that this 'bottom line' can take the form of quantum logic gates such as Toffoli gates. Quantum computation is, of course, a very hot topic at present because of the hope that it may soon be possible to construct artificial quantum computers. Accessible accounts of such computation have been provided by, among others, Milburn (1998) and Lo, Popescu and Spiller (1998). Many 'quantum computation in the brain' approaches envisage the occurrence of large-scale quantum coherence in the brain extending across many neurons or even the whole brain. Mine has the advantage that, being at the basis of a mainly classical fractal structure, the quantum coherence itself needs to be maintained for only short periods over areas no greater than part of a single cell membrane (Bieberich, 1999, 2000). Particularly if envisaged as coherence between spin of molecules associated with ion channels, it seems likely that such relatively small-scale quantum structures must arise naturally. They will therefore have become available for exploitation by evolution as soon as they arose. The larger scale coherence required by other models presents greater theoretical problems.
 

My analysis of the Liar paradox depends on examining its separate, atomistic components in the context both of the holistic 'field' provided by an undivided, experiencing consciousness, and of, first classical Boolean logic, followed by quantum logic. I show that both of these logics are inadequate to account for our experience of paradox. It emerges, however, that a combination of quantum logic and fractal topology can accommodate our experience, hence suggesting that our minds do incorporate these principles. The details are inevitably somewhat technical, but I hope readers who do not have much familiarity with these topics will nevertheless be able to follow the argument. Reference to the figures is probably essential to understanding the text. There are also appendices describing the basics of quantum computation and fractal topology for people unfamiliar with them.
 
 

Classical (Boolean) analysis

Let's express the Liar paradox in the form, 'I am a Cretan and all Cretans are liars'. Epimenides' provenance is thus an accessible statement. Here are two sets of definitions:
 

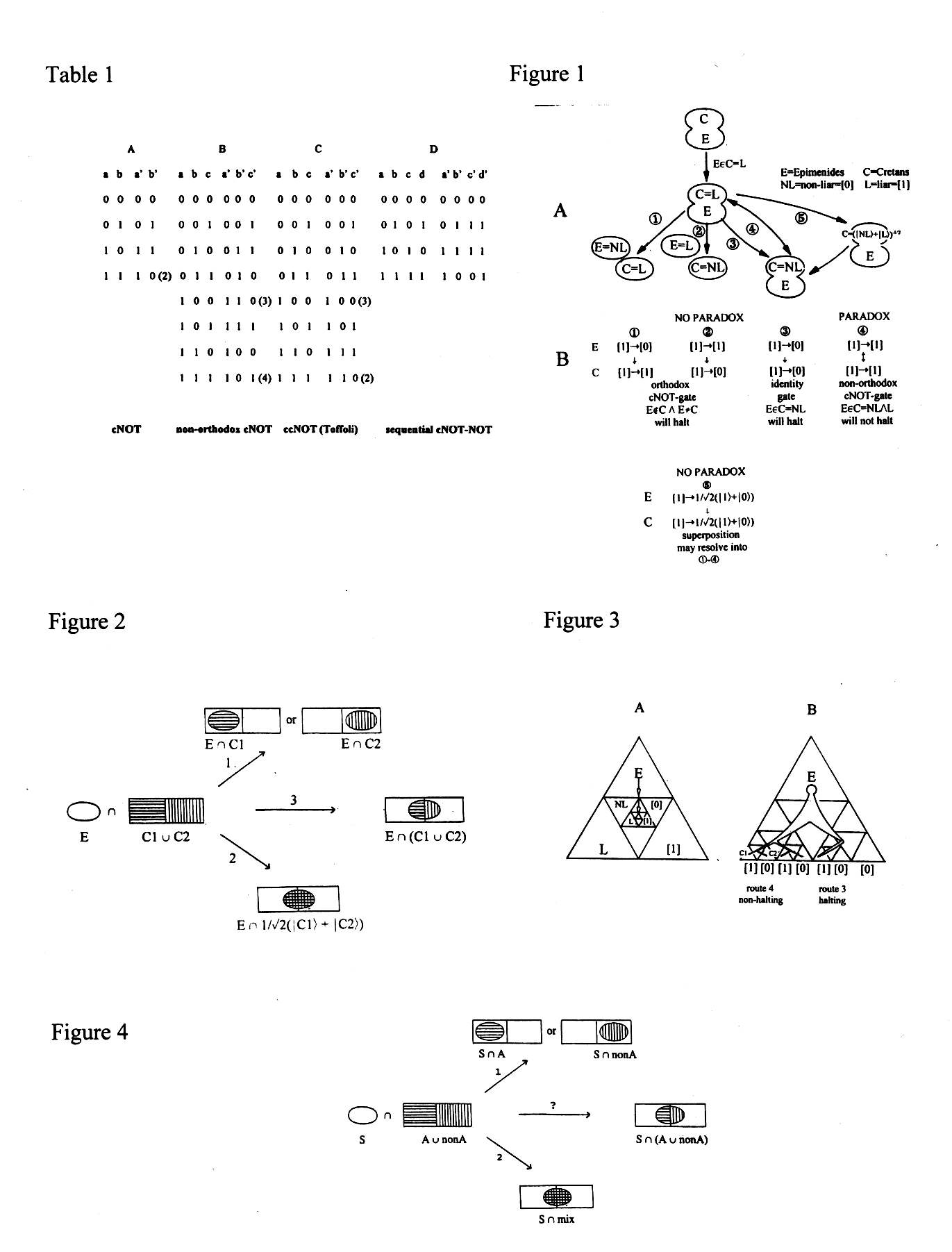
(1) E = Epimenides is an element of set C = Cretan or of set NC = non-Cretan (E is element of C or NC). C may be L = Liar or NL = non-Liar (C = L or NL). For illustration see Fig. 1; in this figure everything outside of C is not defined as exclusively either L or NL.
 

(2) If E = L then a NOT-operation will change the value of each statement made by E.

The Liar paradox can be taken to start with E is element of C and C = L. Due to a NOT-operation the value of each statement made by E will change. E now belongs to NC and C = L or NL (Routes 1 and 2 in Fig. 1). If E is in NC the paradox is resolved by Epimenides being a liar when claiming to be in C (route 2) or truthful about being NC (Route 1. Note that one can still suppose, if one wishes, that he may be lying about the propensities of all Cretans). In contrast, when E does belong to C, the paradox will be iterated ad infinitum via a combination of Routes 3 and 4. Route 3 on its own would allow termination of the computation as the registers would simply set to the condition of Epimenides being both C and NL, but in practice the computation must always be re-started no sooner than finished due to the route 4-loop. These are the characteristics of a classical or atomistic computation.
 

In the literature, a solution of the Liar paradox has been attempted by avoiding the self-referential negation inherent to the original postulate (Tarski, 1969; Yablo, 1993). Their approach involves excluding the statement of E from the truth-value of statements on set C, or in other words, E 'escapes' to a meta-set by temporarily becoming a non-Cretan when making a statement on C. It has been shown that there are only two ways in classical computation to restore the state of E being element of C. One is simply to include a third axiom which says that upon any statement E is no longer member of C but will be reclaimed as Cretan afterwards. This is equivalent to route 1, however, the third axiom forces E back on route 4. Hence, there is no difference to the infinite iteration of routes 3 and 4. Yablo has tried to remove the self-reference by constructing an infinite series of Cretan sets with E always making the liar statement on the next following set that he is not a member of (Sorensen, 1998; Yablo, 1993). However the Liar paradox, even without immediate self-reference, nevertheless stays paradoxical when E's statement is repeated infinitely. In these circumstances we do not know whether Epimenides is a liar or not because we cannot stop the computation. So the best we can do is to introduce a multi-valued logic: E is a liar (E = L), or is not a liar (E = NL), or is a state in between both, a liar and a non-liar (E = L + NL). The latter state takes us immediately to the next analysis of the Liar paradox discussing Epimenides being both, a liar and non-liar by means of quantum-mechanical superposition of states.
 

Quantum logical analysis
 

If we assign the truth values so that [1] = L and [0] = [NL] to E or C, it is possible to deal with them in quantum logical cNOT (i.e. controlled NOT) operation with the q-bit (i.e. quantum-bit) spin values [1] and [0]. Readers wanting a technical description of this quantum logical operation are referred to Appendix 1. In brief, E and C are two quantum registers with one control and target q-bit in each register. In quantum logical operations, spin value changes of the control q-bit are intertwined (i.e. entangled) with those of the target q-bit. If we start with E housing the the control q-bit that determines the output of the target q-bit in C, then the transitions resulting from routes 1 and 2 are compatible with an orthodox cNOT gate (see Fig. 1). C changes its truth value only if E stays [1]. E is then not an element of C any longer because being a liar changes his physical state of being a Cretan (i.e. E is element of NC = [0] = NL and C = [1] = L, or E is element of NC = [1] = L and C = [0] = NL. In contrast, route 3 expresses the operation of an identity gate (E is element of C and both E, C = [0] = NL). Here the truth value is the same in both registers and there is no lie to be told. Routes 1 to 3 are not paradoxical so the operation will halt without negation of its own truth value. Repeat operations will occur only if the orthodox cNOT gate is re-booted, so to speak, from without.
 

So far, the computational results of a quantum logical cNOT-gate are not different from those of a Boolean gate. E may escape the paradox by becoming an element of the meta-set NC, however, the operation is either infinitely repeated or E adopts the truth-value [0] = NL for good. The paradox arises from the combination of route 3 and 4 which looks like another identity gate, but shows mutual negation of the truth values of E and C (Fig. 1). This negation is what distinguishes route 4 from the orthodox identity gate of route 3. It results in a non-halting computation due to infinite repetition of the negation from within the operation itself. The necessary quantum logical operation can be implemented by the non-orthodox cNOT gate described in Appendix 1. As shown in Fig. 1, a gate of this type can accommodate a quantum superposition of [0] and [1] in each of the two registers (route 5). The superposition of L and NL itself is non-paradoxical for as long as it remains 'unmeasured'. A measurement of the truth value of E and C, however, would be non-paradoxical only if E and C shared the same truth value within each of their registers, so allowing the computation to halt via a combination of routes 5 and 3. A combination of routes 5 and 4, on the other hand, will be paradoxical and non-halting in the same way as the combination of 3 and 4. Recently, Aerts et al. have analyzed the liar paradox by quantum mechanics reporting the appearance of the truth values L and NL from a superposition of the two state (Aerts et al., 1999). However, my analysis by implementation of quantum logical gates has shown that a superposition of complementary spin a.k.a. truth values cannot be a solution of the liar paradox without introduction of a previously unknown non-orthodox cNOT gate.
 

It might be supposed that the suggested combination of routes 5 and 4 is just a flight of fancy, perhaps analogous to the idea of a perpetual motion machine forever unrealizable because violating the laws of thermodynamics. Unlike perpetual motion, however, the non-orthodox cNOT gate does not violate physical laws. In particular, its reversibility characterizes it as a quantum logical gate (see Appendix 1). An adequate technical realization is possible by inclusion of a third, auxiliary q-bit (A) into the logical chain: if for E: [1] changes to [1], then for A:[1] changes to [0], then for C: [1] changes to [1]. Note, that the truth value of A is excluded from the set of accessible (measurable) results. Otherwise the computation will halt as with a combination of route 5 and 3 resulting in an identity operation. The exclusion of results from their accessibility does not violate physical laws but renders the non-orthodox cNOT gate distinct from a sequential computation as implemented by coupled orthodox cNOT-gates (see Appendix 1).
 

It is intriguing to note that, if the accessibility of truth value A = [0] is not permitted, there is no way of discriminating E and C by telling a lie. In other words, Nature may know a lie in these circumstances but cannot tell us of Her knowledge through measurement. The concept of a lie is dependent upon knowledge of the truth. It is thus possible to conclude that no classical or quantum approach to the solution of the liar paradox is able to handle the simultaneous existence of a truth value and its negation in the context of a set of results with only one truth value. Nevertheless, the simultaneous accessibility of E = L and E = NL in our own minds proves that this set exists. In order to understand how the set can exist, and to characterize the nature of a non-orthodox cNOT gate, we need to move on to a topological approach to the paradox.
 

Topological analysis

Any classical or quantum measurement of a truth value requires its mapping into a real space and an at least temporary correlation to the measurement instrument within this space. This applies to discerning truth values along with all other measurements. Figure 2 shows that Epimenides' statements can be represented by a mapping of E into two sub-spaces (C1 = NL and C2 = L) within the group of Cretans. Assuming that any contradiction to the exclusivity of C's truth value is only temporary, finding an appropriate operation for resolving the paradox involves mapping Epimenides onto either C1, or C2, or both together via a superposition of L and NL. But, if the superposition is measured, Epimenides' space will be split into E mapped onto C1, or E mapped onto C2, with C1 intersected with C2 = 0 (The respective product set contains all elements which are both, member of E and C1 or C2, or member of C1 and C2, respectively. If C1 intersected with C2 = 0 then the intersection set is empty). As before, we either exclude Epimenides from the space which equals his truth value (routes 1 or 2 in the previous section), or we include him and enter the paradox (route 3 looping with 4 or 5).
 

Is there any possibility that E could be in two spaces (C1 and C2) at the same time without invoking a superposition of L and NL? As it happens, there is. C and NC can be described as sub-spaces of a fractal, or self-similar structure (Barnsley, 1993, Peitgen et al., 1992). A brief account for such spaces is given in Appendix 2. It turns out that the sub-spaces of a fractal show the following characteristics: C1 unequals C2 and C1 intersected with C2 unequals 0 (note the different second term here from the one describing non-fractal sub-spaces given in the previous paragraph). As shown in Fig. 3A each sub-space of a Sierpinski triangle (which is a typical, simple fractal) contains the other sub-space(s) due to iterative downscaling of the whole structure into each part.
 

The process of mapping E can now be pictured as E entering the bottom triangles of Fig. 3B through two slits (a fractal double-slit). One can see that mapping E onto C1 or C2 involves simultaneous mapping onto the other sub-space of the growing fractal. If E is assigned to the central triangle and controls a cNOT operation on target registers in the bottom triangle, we have the requisite fractal cNOT gate (see Appendix 1 for more detail).
 

Figure 3B shows that the non-halting operation (routes 4 and 5 in the previous section) is describable as an ongoing mapping of E into two sub-spaces (C1 and C2) of an emerging fractal. Since E is always in the central triangle, this implies a repeated copying of the control register into sub-spaces of the target register accompanying iterative tiling of the Sierpinski triangle. The control q-bits are multiplying along with proliferation of the sub-spaces inside the target registers as the computation proceeds. It should be noted, however, that the total computation does not proceed by sequential steps but happens simultaneously in each sub-space of the fractal. The overall picture is of a computation whose different forms "percolate", so to speak, into different sub-spaces of a fractal tree where they can proceed independently while nevertheless remaining related to one another within an all encompassing structure.
 

A surprising conclusion is that halting and non-halting operations can be discriminated if non-halting requires an equal percolation of E into all sub-spaces of the growing fractal (iteration of route 4). If there is not equal percolation, one computation outgrows the other and hence tends to exclude the other from sub-spaces further down the line. After allowing sufficient time for evolution of the fractal, a discrimination can be made by simply counting the truth values as spin states ([0] = NL and [1] = L) in the bottom triangles (Fig. 3B). The ratio [1]/([1] + [0]) will be 0.5 in case of the non-halting operation whereas it asymptotically reaches 0 otherwise. The first case is identical to the result of a non-orthodox cNOT gate described as an algorithm for the liar paradox in the previous section. An implementation of this algorithm by a fractal can thus decide on whether an operation creates a "true" paradox (route 4) or whether a finalization of the operation occurs (branches of the fractal tree "die out" or route 3).

Penrose has suggested a similar operation for solving the Thue word problem (Penrose, 1989; see Dewdney for review,1989). In brief, his idea of a fractal computer (equivalent to the fractal double slit) can substitute any string of symbols in a finite time, no matter how long they are. This is the result of a progression toward shorter operation cycles eventually asymptotically reaching a finite duration for the complete computation. The fractal cNOT gate is also an operation asymptotically reaching a finite duration time for a computational result. Similar to Penrose's computer the halting of a calculation prevents further branching of the fractal tree. The difference to his model, however, is given by the evolution of the fractal occurring simultaneously with the computation. Penrose's fractal computer has an infinite structure a priori whereas the evolution of the fractal cNOT gate is intrinsically determined by the nature of the computation (halting or non-halting) itself.
 

Do fractal gates exist in our brains?
 

A problem with the fractal gate proposal arises from the fact that there is no internal evidence in my analysis so far to unequivocally show that we must posses such gates. As is shown in Appendix 1, for instance, the output from two orthodox (Toffoli) cNOT gates can mimic the output of my proposed fractal cNOT gate, at least in the case of halting operations. More generally, it is always possible to devise some other architecture which could carry out the same formal operations as the fractal gate (except in relation to the secondary operation which may solve the halting problem. However, there is no good evidence that our minds can in fact sometimes solve this problem). The concept of fractal computation does have other attractions though, especially as fractality is known to be involved in so many aspects of brain function. I would like to briefly mention some other considerations, which suggest that the idea is worth taking seriously. More detailed accounts are available elsewhere (Bieberich, 1999 a-d).
 

In this paper, I have tried to analyze a 'self-negation' paradox in terms of orthodox classical or quantum mechanical models of computations that might underpin consciousness. In both cases a single event perceived in a Cartesian space of consciousness is a local and point-like signal, distinct from any other event once the 'computation' has been accomplished. Despite tremendous progress in modern neuroscience there are no valid topological concepts relating a neurophysiological activity to a simultaneous conscious perception. Hence, it is suggested that the standard concept of point-like events distributed in a Cartesian space has to be abandoned in favor of a fractal concept of space containing the whole in each part.
 

As shown in Fig. 4, classical models based on pinball-like collisions of neurotransmitters with particular receptors in the nerve cell membrane will relate an inner observer "S" either to event "A" or "nonA" in a Cartesian space underlying the topology of neuronal or sub-neuronal anatomy and molecular morphology. Accordingly, the inner observer will be split into as many disjoint sub-entities as there are events perceived. Obviously, this model is equivalent to the mapping of Epimenides onto the sub-spaces C1 or C2 in Fig. 2A. A holistic and undivided perception may be preserved by a quantum mechanical interpretation as given by a superposition of "A" and "nonA". A superposition, however, will result in a mixture of indistinguishable perceptions homogeneously distributed in the perception space. This is contradictory to our conscious experience of a world consisting of distinct objects. A resolution by measurement of eigenstates does not provide a solution of this dilemma since it converts an initial superposition into a classical distribution of states. This is another apparent paradox, of a sort.
 

Resolution of this new paradox seems to require a fundamental change in our concept of space in relation to consciousness. Recently, two models have been suggested for embedding consciousness in a configuration space that is either based on intrinsic contextuality or putative signal non-locality of entangled quantum states (Aerts et al., 1999; Sarfatti, 1998). The two models cope with non-local volition of an inner observer by locally acting on neuronal events. However, the local activity is still bound to the distribution of the neuronal substrate in a Cartesian space. Accordingly, a correlation of a consciously experienced perception to a neuronal event has again to face a topological paradox due to the separability of the substrate. This correlation will render any computation performed by the human mind as atomistic as with classical or orthodox quantum mechanical models.
 

In the present study, the Cartesian concept of space is abandoned and replaced by a fractal structure containing the whole in each part. A fractal space underlying the topology of quantum registers may cope with a computational solution of the Liar paradox and the Halting problem. In addition, mapping an inner observer onto a fractal perception space is consistent with the view that computation in the human mind is relying on fractal cNOT gates. The analysis of the Liar paradox has shown that the classical view of an atomistic particle distribution in a Cartesian space cannot cope with the physics required for a description of the human mind. Furthermore, a quantum mechanical approach will stay incomplete if not combined with a topological concept for the non-Cartesian distribution of its quantum states. Further studies are needed on the applicability of the fractal concept to the solution of other paradoxes arising from the atomistic nature of our percepts.
 

Acknowledgments: The author is gratefully indebted to Dr. Chris Nunn who gave invaluable support by thoroughly discussing the present study and critically reading the manuscript.

References
 

Aerts, D., Broekert, J., and Gabora, L. (1999) Nonclassical contextuality in cognition: Borrowing

from quantum mechanical approaches to indeterminism and observer dependence. http://hubcap.clemson.edu/psych/Dialogues/10.0html

Barnsley, M.F. (1993) Fractals everywhere. Academic Press, Cambridge, MA.

Bieberich, E. (1999a) Structure in human consciousness: A fractal approach to the topology of the self perceiving and outer world in an inner space. http://cogprints.soton.ac.uk/abs/neuro/199902004

Bieberich, E. (1999b) Non-local quantum evolution of entangled ensemble states in neural nets and its significance for brain function and a theory of consciousness. http://xxx.lanl.gov/html/quant-ph/9906011.

Bieberich, E. (1999c) Generation of a conscious self in a fractal quantum oscillator (FRAQTOR) J. Consciousness Studies Abstracts Flagstaff conference "Quantum Approaches to Consciousness", p. 23-24. Also accessible at . http://www.bakery.demon.co.uk/flagstaff/abstracts.htm

Bieberich, E. (1999d) In search of a neuronal substrate of the human mind: new concepts from topological neurochemistry. http://cogprints.soton.ac.uk/abs/neuro/199902006

Bieberich, E. (2000) Principles of neural quantum computation and classical communication: Darwinian evolution of the human mind in the quantum dynamical brain. J. Consciousness Stud. Abstracts Tucson 2000, p. 88.

Chaitin, G.J. (1999) The unknowable. Springer, New York, NY.

Dewdney, A.K. (1989) Computer Recreations. Scientific American 12, 140-142.

Faletta, N. (1990) The Paradoxicon. John Wiley & Sons, New York, NY.

Gilburn, G.J. (1998) The Feynman processor. Perseus Books, Reading, MA.

King, C.C. (1995) Fractal neurodynamics and quantum chaos: Resolving the mind-brain paradox through novel biophysics in "Fractals of brain, fractals of mind" (MacCormack, E. and Stamenov, M.I., eds.) John Benjamins, Amsterdam and Philadelphia.

Lo, H-K., Popescu, S., and Spiller, T. (1998) Introduction to quantum information and computation. World Scientific, Singapore.

Penrose, R. (1989) The emperor's new mind. Oxford University Press Inc., New York, NY.

Penrose, R. (1994) Shadows of the mind. Oxford University Press Inc., New York, NY.

Peitgen, H.-O., Jürgen, H., and Saupe, D. (1992) Chaos and Fractals, New Frontiers in Science. Springer-Verlag, New York, NY.

Rieffel, E. and Polak, W. (1998) An Introduction to Quantum Computing for Non-Physicists. http://xxx.lanl.gov/html/quant-ph/9809016

Rosen, R. (1993) Drawing the boundary between subject and object: comments on the mind-brain problem. Theor. Med. 14, 89-100.

Sarfatti, J. (1998) The post-quantum physics of consciousness.

http://www.qedcorp.com/pcr/pcr/pq/pq.htm

Searle, J.R. (1997) Mystery of consciousness. The New York Review of Books, NY, p. 89-93.

Sorensen, R.A. (1998) Yablo's paradox and kindred infinite liars. Mind 107/425, 137-155.

Stapp, H. (1995) Why classical mechanics cannot naturally accommodate consciousness but quantum mechanics can. Psyche 2(5).

Tarski, A. (1969) Truth and proof. Scientific American 6, 63-77.

Turing, A.M. (1937) On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 42, 230-265, correction 43, 544-546.

Vedra, V. and Plenio, M.B. (1998) The Basics of Quantum Computation.

http://xxx.lanl.gov/html/quant-ph/9802065

Yablo, S. (1993) Paradox without self-reference. Analysis 53, 251-252.
 

Appendix 1
 

The orthodox and non-orthodox cNOT-gate
 

The hallmark distinguishing a quantum logical from a classical (Boolean) computation is its reversibility. The classical OR-gate is irreversible (cannot run backwards) since it is impossible to unambiguously infer the input of two bits from their output states (e.g., if output is [1,1] the input can be [0,1], [1,0], or [1,1]). A cNOT-gate consists of a control and target qubit implementing an OR-operation with the input and output spin values [0] and [1] as shown in A (for instructive review see Vedral and Plenio, 1998). If the input [1] of the control qubit equals its output the target qubit changes from [0] to [1] or vice versa. This operation is reversible since the input value of the control qubit can be unambiguously determined from the output of the target qubit (input and output are interchangeable by implementation of the reverse operation). It can be seen as "copy-operation" in the sense that the target qubit with input [0] has the same output [1] as the control qubit (single NOT-operation). The non-orthodox cNOT gate can be constructed from three qubits with [a] as control qubit for [b] and [b] as control qubit for [c] (B). This gate carries out a "copy operation" from [a] on [c] if [1] is given as input for the two qubits (NOT-NOT-operation). In consequence, the output of a non-orthodox cNOT-gate is equivalent to an identity gate. The difference to an orthodox Toffoli gate with three qubits ([a] and [b] are control, [c] is target qubit) is shown in C. The result is also different from an orthodox cNOT-NOT-gate with sequential operation from [a] on [b] and [b] on [d]. This gate can be constructed with four qbits ([a] and [b]: cNOT1, [b] and [c]: identity gate, [c] and [d]: cNOT2) as shown in D. Although the operation resembles B, the sequential cNOT-NOT-gate is not reversible since output and input are not interchangeable. The numbers indicate the routes shown in Fig. 1. Route 1 and 2 are identical due to reversibility of the operation. Route 5 is not shown since only orthogonal results (after accomplishment of the unitary evolution) are denoted.

[Table is presented as Figure "Table 1" in HTML-format].
 

Appendix 2
 

Topology of fractal space
 

A self-similar or fractal structure is generated by iterative mapping of each point of a compact point set A on a space X into a sub-space X_i by linear affine transformation (Hutchinson operator, Barnsley, 1993; Peitgen et al., 1992). The Sierpinski triangle in Fig. 2 can be constructed by iterative translation of each vertex point along the edges followed by rotation of the edges by 60°. A downscaling factor warrants a tiling operation into four equally sized inner triangles forming the sub-spaces X_i of the fractal. The fractal space is a metric space with a positive distance function for each point of the sub-sets: X₁-X₂ unequals 0. However, the sub-sets Ai cannot be separated: A₁ intersected with A₂ unequals 0. This results in the scale invariance or self-similarity of the fractal: A = sA with s=scaling factor. As shown in Fig. 2 each inner triangle contains the whole structure as a downscaled part. Self-similarity distinguishes the fractal space from any other metric space.
 
 

Legends to the Figures
 

Figure 1
 

Analysis of the Liar paradox by classical and quantum logic
 

Epimenides (E) states "I am a Cretan" (E is element of C) and "All Cretans are liars" (C = L). Due to the Liar statement routes 1-3 implement a NOT-operation. E becomes a non-Cretan (routes 1 or 2) and may be a non-liar (NL) or a liar (L). The operation equals an orthodox cNOT-gate (see Appendix 1) and halts without entering a paradox. If E stays Cretan the Cretans have to convert to non-liars (route 3) in order to avoid a paradox. Again, the operation halts, this time by implementation of an identity gate. However, if E stays Cretan and non-liar the mere possibility to utter a negation of a truth-value already creates a paradox. The Cretans oscillate between C = L and NL ad infinitum (route 4), the operation does not halt. Route 4 can be implemented by a non-orthodox cNOT gate (see Appendix 1). The necessary quantum-superposition is indicated by route 5 and can resolve into the truth-values of routes 1 to 4. Boolean symbols: = and, = or; the notation (bra-ket) in route 5 is technical and denotes a superposition state.
 

Figure 2
 

Topological analysis of the Liar paradox
 

Epimenides (E) is mapped onto the space X (C) = C1 in union with C2 (for comparison see Appendix 2). The mapping operation 1 will correlate E either to C1 or C2. The consequence is a splitting of the space in which the Cretans live (equivalent to routes 1 or 2 in Fig. 1). A superposition of E with C1 and C2 is achieved by the mapping operation 2 (equivalent to route 5 in Fig. 1). However, C1 is no longer separable from C2. A simultaneous mapping of E onto C1 and C2 is indicated by the operation 3.

Symbols in set theory: = intersection, = union.
 

Figure 3
 

Fractal cNOT-gate
 

Fractal construction of the space X (C). In A it is shown that Epimenides = E is mapped into a space which iteratively contains the opposite truth value as a subspace. As shown in B, the fractal distribution of quantum states into the sub-spaces of a Sierpinski triangle may be used for implementation of a non-orthodox cNOT gate. A quantum computation will proceed with E as control qubit percolating into the target registers (bottom triangles) by iterative tiling of its sub-spaces. The fractal cNOT-gate can distinguish a non-halting (equivalent to route 4) from a halting operation (route 3) by counting the spin values in the target registers (Appendix 1).
 

Figure 4
 

Mapping of an inner observer onto a perception space in consciousness
 

An inner observer (S) is aware of a perception space filled with an object (A) and all the other objects (nonA). A one-to-one mapping will split S into S1 aware of A and S2 aware of nonA (1). This is equivalent to the mapping operation 1 in Fig. 2. If the undividedness of S is preserved the objects A and nonA will be superimposed but not longer separable (2). Mapping 3 describes the observation of objects in human consciousness: S is inseparable but A and nonA are separable.