Modelling Emotions with Multidimensional Logic
Carlos Gershenson
Fundación Arturo Rosenblueth
Insurgentes Sur #670, Del Valle
México City, México
carlos@jlagunez.iquimica.unam.mx
Abstract
One of the objectives of Artificial Intelligence has been the modelling of "human" characteristics, such as emotions, behaviour, conscience, etc. But in such characteristics we might find certain degree of contradiction. Previous work on modelling emotions and its problems are reviewed. A model for emotions is proposed using multidimensional logic, which handles the degree of contradiction that emotions might have. The model is oriented to simulate emotions in artificial societies. The proposed solution is also generalized for actions which might overcome contradiction (conflictive goals in agents, for example.).
1. Introduction
We believe that for modelling intelligence successfully, not only the "reasonable" (logic, planning, language, etc.) part of the human mind must be modelled. We believe that also other human characteristics which at firsthand would appear to have little to do with intelligence (or at least have been less studied in Artificial Intelligence that the "reasonable" ones), such as emotions, behaviour, conscience, etc.; must be modelled in order to have a more complete intelligence model, since they affect the mind.
Marvin Minsky, in his Society of Mind [4], remarks about the possibility of machines having emotions: "The question is not whether intelligent machines can have any emotions, but whether machines can be intelligent without any emotions." In this context, we find very important the simulation of emotions for a computer system to be not only intelligent, but also believable [2]. It has also been said before that emotions are integral to human perception [7], and that they are strongly connected with goal achieving or failure [5]. So, for simulating human intelligence and intelligent societies, it is essential that emotions are modelled.
But too often emotions carry certain contradiction. For example, if your loved one cheats on you, we could say it makes you hate him or her. But that doesn't mean you stop loving him or her immediately. You feel love and hate for your loved one at the same time. Agreeing that love is opposite to hate, we find very hard to model this contradiction with a traditional logic (we say that it's traditional a logic which states that something can't be true and false at the same time). This is why we use multidimensional logic.
This paper is organized as follows. The next section presents a brief introduction to multidimensional logic [3]. Section 3 presents a critic overview of previous work in the modelling of emotions. With this background, Section 4 presents the model of emotions we developed using multidimensional logic, and then the model is generalized for events in which contradiction might overcome. Finally, we discuss in Section 5 the advantages and disadvantages of this model.
2. Multidimensional logic
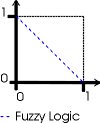
Multidimensional logic [3] is a paraconsistent logic. A logic is said to be paraconsistent if it admits that a conclusion may be obtained from contradictory premises [8]. This means, that multidimensional logic admits contradictions and paradoxes. Multidimensional logic states that one statement may have more than one truth value. It represents different values in a truth vector, in which each value may be fuzzy [9]. It is useful when the values of a truth vector represent opposites. For example, we could use a bidimensional logic representing (true, false), as in Figure 1.
So, we have a bidimensional vector, with one axis representing truthness, and other its opposite, falseness. The dotted line which goes from the point (1,0) to the point (0,1) represents fuzzy logic. This is, where a value complements it's opposite, and there's no contradiction. In this paper we will limit ourselves in bidimensional logic.
We define a bidimensional logic variable (bdlv) as:
X is a bdlv if and only if X M={(x,y) | x,y [0,1]}
Returning to our cheating example, we could model part of the emotions of the cheated one with a vector representing (love/hate). Let's say his love/hate for his or her loved one is (0.8, 0.95). Note that this is equivalent to a love/hate of (0.05, 0.2). This is represented nicely since a value doesn't affect its opposite, as in traditional logics.

Figure 1. Representation of a bidimensional logic variable.
We define the bidimensional logical operators AND (&), OR(|) (inclusive), and NOT(~) as follows:
(x1,y1) & (x2,y2) = (min(x1,x2), min(y1,y2))
(x1,y1) | (x2,y2) = (max(x1,x2), max(y1,y2))
~(x,y) = (1-x, 1-y)
These operators are based in Zadeh's operators of fuzzy logic [9]. All other logical operators may be obtained as equivalences of combinations of these.
We will now define other three operators characteristic of multidimensional logic: equivalence, degree of contradiction, and projection.
If the plane is "flipped"over the fuzzy line, the points that would be next to each other, would be equivalent. For example, (0,0) and (1,1) are equivalent. This is because if falseness is 0, then truthness is 1, and if truthness is 0, falseness is 1. The same happens with (0.25,1) and (0, 0.75). We can define the operator equivalence E as:
E(x,y)=(1-y,1-x)
Note that vectors with no contradiction, don't have an equivalent different that themselves. Also note that for all points in the line x=y, its negation is the same as its equivalent. And since (0.5,0.5) is its own equivalent, because it is the fuzzy line, it is also its own negation. Furthermore, note that
E(x,y)=(~y,~x)
A & B = E(A | B)
A | B = E(A & B)
We can define the degree of contradiction C with:
C(x,y)=|(x+y)-1|
C can be seen as "how far do you get from fuzzy logic". If C is 0, then the point belongs to the fuzzy line, there's no contradiction, and it is contained by fuzzy logic. As C increases, you go farther from the fuzzy line, until you reach total contradiction (C=1). With C, we can see "how contradictory" a proposition is.
For defining the projection P of bidimensional logic in fuzzy logic, we can use as an example the values of something that's white AND black at the same time, or none of them (Figure 2).
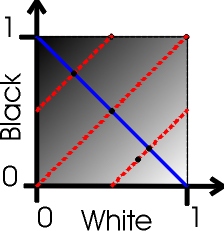
Figure 2. BDLV (white, black)
If white is 0, then it is considered as black. If black is 0, it is considered as white. Here it might seem that all points of a line parallel to y=x are equivalent. This is because black and white are added, but we can't see in the graphic its total amount of contradiction. For example, in (1,1), we say that we have 100% of white and 100% of black. This gives us gray. The same tone of gray as in (0.5,0.5) But it's not the same 100% gray than 200% gray.
We can also observe the projection of bidimensional logic in fuzzy logic. This is, the "tone" of truthness the contradiction we would have in fuzzy logic. But as we said, it is not equivalent. We can find the projection by making a line that passes through the point we want to project, and parallel to y=x. Then, the projection would be its intersection with the fuzzy line. So we have that:
P(x,y) = ((x-y+1)/2,(y-x+1)/2)
For a more detailed definition of multidimensional logic, it's operators and properties, please refer to [3].
3. Previous work on emotions
In the Oz project, guided by Joseph Bates at Carnegie Mellon University, was first introduced the term of believable agent. They are intended to provide the illusion of life. One central requirement for them to be believable is that they express emotions [2]. They base the modelling of emotions mainly in the cognitive structure of emotions proposed by Ortony, Collins, and Clore (OCC) [6].
OCC divide emotions by whether they involve reactions to events, agents, or objects, constructed with goals, standards and attitudes, respectively. Then, under these, emotions are categorized.
In the Oz project, the next basic emotions are used: joy, distress, hope, fear, pride, shame, admiration, reproach, love and hate. Gratification, gratitude, remorse and anger are modelled as combinations of the basic emotions.
One problem with this model is that all emotions are crisp. This is, an agent may be only, for example, afraid or not afraid. The agent can't have different degrees of fear. Also, the same kinds of emotions are used for every agent. And in our common life, not every person has the same conception of each emotion (different reactions to the same emotions). The model itself is good, but these problems arise when one is modelling emotions of individuals in an artificial society.
Mueller and Dyer propose a very interesting computational theory of daydreaming [5], and it is implemented in the program Daydreamer. "Daydreaming is the spontaneous human activity of recalling or imagining personal or vicarious experiences in the past or future".
An essential part of Daydreamer is the emotion component, in which daydreams initiate, and are initiated by emotional states arising from goal structures. Emotions also activate, in part, control goals.
Among the emotions handled by Daydreamer, are anger, embarrassment, disappointment, rejection, fear, retaliation, and rejection.
Again, it is a very good model for an individual, but the same problems of Oz and OCC arise here: emotions are crisp, and every emotion would be modelled the same way for every individual in an artificial society.
Also emotions are very well defined, which doesn't give any ambiguity we believe emotions would have. This is, not everyone may agree that the conditions of shame, for example, are the same they have. We believe that certain ambiguity is needed so that people with slight differences in their concept of emotions understand which emotion we are talking about without starting an argument on how should that emotion be felt.
4. Model of emotions
We will use three sets of emotions represented by a bidimensional logic variable each: love/hate, joy/grief, and happy/sadness. This will be our basic emotions, and we will develop other emotions in terms and combinations of these.
We find some hazard in finding specific definitions (and thus, boundaries), to these emotions. So we will set them in a third axis, so we can fuzzify their boundaries too, as seen in Figure 3.
Figure 3. Model of emotions.
So, the x axis represents positive emotions, the y axis negative ones, and we order our specific emotions in the z axis arbitrarily. We could insert more emotions, but we find these three enough to satisfy our purposes. So, we can see that in the z axis, the zero represents love/hate, the one joy/grief, the two happy/sadness, and the three love/hate again. This makes the z axis cyclic. This is helpful for representing emotions between love/hate and joy/grief and between love/hate and happy/sadness.
An example of some emotions represented in this model is shown in Table 1, and plotted in Figures 4 and 5.
| Emotion | Vector |
| love | near (1,0,0) |
| hate | near (0,1,0) |
| indifference | near (0.5,0.5,0) |
| joy | near (1,0,1) |
| grief | near (0,1,1) |
| boredom | near (0.5,0.5,1) |
| happiness | near (1,0,2) |
| sadness | near (0,1,2) |
| conformity | near (0.5,0.5,2) |
| ecstasy | near (1,0.5,0.3) |
| rage | near (0.4,1,1.5) |
| pride | near (1,0,1.5) |
| shame | near (0,1,1.5) |
| anger | near (0,1,2.5) |
| jealousy | near (1,0.8,0) |
| lust | near (0.8,0.3,2.7) |
| sorrow | near (0,1,0.5) |
| revenge | near (0.5,1,0.5) |
| tenderness | near (1,0.2,2.3) |
| enthusiasm | near (1,0,1.3) |
| surprise | near (0.8,0.8,2) |
Table 1. Emotions represented with the model.
We express the vector in the form near (x,y,z) because not every individual of a society has the same emotion definitions. For example, A can be happy and B also, but they may not feel and act in respect to their emotions in the same way. They have strictly different emotions, but they are both considered as happiness. In an artificial society, we would set slightly different emotion vectors for each individual.
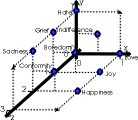
Figure 4. Emotions represented with the model.
The form near (x,y,z) can be seen as an open ball. An open ball around a vector X is defined as all the points which distance to X is lesser than a radius r. We can define an open ball in terms of a fuzzy membership function. So, for an emotional vector A, its degree of the emotion X would be:
1 if |X-A|<=0.1
1-(10*(|X-A|-0.1)) if 0.1<|X-A|<0.2
0 if 0.2<=|X-A|
This means that if the distance from A to X is lesser or equal than 0.1, A is considered as being the emotion X. Then, as the distance increases, A is considered still an emotion X, but in less degree, until finally it has no degree of X at all.
This is also useful for having more than one emotion we are defining at a time. For example, the point (1,0,1.45) would represent 0.5 of enthusiasm and 1 of pride (Table 1, Figure 5). The radius of the open balls may be increased in order to represent many emotions at a time, or be decreased for a crisper model.
An individual would have two kinds of emotion vectors, one for himself, and one for other individual. This would differentiate emotions towards oneself and towards others.
Table 1 is just an example of how can emotions be mapped in the proposed model. New emotions can be mapped according to one's interests, even with different emotions set in the z axis.
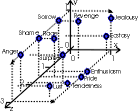
Figure 5. Emotions represented with the model.
A similar model as the one proposed for emotions might be also effective in other areas, such as resolving conflictive goals in agents. Basing ourselves in Figure 1, we would just represent opposite or contradictory goals in the z axis, and after plotting a goal state, either:
A) For a "winner takes all" (crisp) decision, the most dominant axis (x or y) would win. If the values in the axises are equal, declare a third state (no one wins), or choose one value randomly.
B) For fuzzy rules, project into fuzzy logic and apply the rules. Or:
C) Multidimensional rules might be also applied. These would be rules in which a value is independent from its opposite (x is independent from y).
The same model may be used in other areas in which might overcome contradictions. There may be already solutions for these problems, such as the use of tables, but we believe that this model might help to understand and model contradictions more effectively.
5. Conclusions
This model will be finally proven only when it is implemented, most probably in the ASIA project. But we believe it to be effective to model fuzzy emotions with a degree of contradiction and for artificial societies, where each individual might have different "concepts of emotions".
We can also see how important are relations that emotions have with other areas of the intellect, such as goal planning, perception, and memory [1].
We should also note the potential laying in multidimensional logic. It's strength and weakness lies in its openness. Strength because it can represent more effectively uncertainty, contradiction, and ambiguity than traditional logics. Weakness, because when there is no contradiction in a system, it may add noise to it. So in this cases, traditional logics are advised to be used.
As we have seen, the proposed model has more flexibility than previous ones, and thus we believe it will be more effective in artificial societies. Although, this model wouldn't be more effective than others for modelling emotions in individuals, and, as with multidimensional logic, it may even add noise to the system.
Another advantage of the model is that it is flexible itself. If we want more emotions to interact, we would just add more dimensions. It can also be used in combination with crisp, fuzzy or multidimensional rules.
We believe that the model helps to enhance our vision of our mind. At the moment we comprehend paradoxes, they stop being contradictory.
6. Acknowledgements
I would like to thank Jaime Lagunez, Miguel Armas, Pedro Pablo González, Roberto Murcio, Jacobo Hernández, the Instituto de Química, Universidad Nacional Autónoma de México and everyone who has criticized and supported this work.
References
[1] Arbib, M. A. Review: The Cognitive Structure of Emotions. Artificial Intelligence, 54: 229-240. Elsevier. 1992.
[2] Bates, J. The role of emotion in believable agents. Communications of the ACM, 37 (7): 122-125. 1994
[3] Gershenson, C. Lógica multidimensional: un modelo de lógica paraconsistente. XI Congreso Nacional ANIEI, Memorias, 132-141. Xalapa, México. 1998.
[4] Minsky, M. L. The Society of Mind. Simon & Shuster, Old Tappan, NJ, 1985.
[5] Mueller, E. T. and Dyer, M. G. Towards a computational theory of human daydreaming. Proceedings of the Seventh Annual Conference of the Cognitive Science Society, 120- 129. Irvine, CA, 1985.
[6] Ortony, A., Clore, G. L., and Collins, A. The Cognitive Structure of Emotions. Cambridge University Press. Cambridge, 1988.
[7] Picard, R. W. Affective Computing. MIT Press. Cambridge, Mass., 1997.
[8] Priest, G. and Tanaka, K. Paraconsistent Logic, Stanford Encyclopedia of Philosophy, 1996.
[9] Zadeh, L. A. Fuzzy Sets, Inf. Control, Vol. 8: 338-53, 1965.

E-mail: carlos@jlagunez.iquimica.unam.mx
Multidimensional Logic resources at: http://132.248.11.4/~carlos/mdl