Learning Appropriate Contexts
Centre for
Policy Modelling,
Manchester Metropolitan University,
Aytoun Building, Autoun Street, Manchester, M1 3GH, UK.
b.edmonds@mmu.ac.uk
http://www.cpm.mmu.ac.uk/~bruce
Abstract. Genetic Programming is extended so that the
solutions being evolved do so in the context of local domains within the total problem domain. This produces a situation where different
“species” of solution develop to exploit different “niches” of the problem –
indicating exploitable solutions. It is
argued that for context to be fully learnable a further step of abstraction
is necessary. Such contexts abstracted
from clusters of solution/model domains make sense of the problem of how to
identify when it is the content of a model is wrong and when it is the
context. Some principles of learning to
identify useful contexts are proposed. Keywords: learning, conditions of
application, context, evolutionary computing, error
1.
Introduction
In AI there have now been many applications of context and context-like
notions with a view to improving the robustness and generality of
inference. In the field of machine
learning applications of context-related notions have been much rarer and, when
they do occur, less fundamental. Inductive learning, evolutionary computing and
reinforcement techniques do not seem to have much use for the notion. There have been some attempts to apply
context detection methods to neural networks, so that a network can more
efficiently learn more than one kind of pattern but these have been limited in
conception to fixes for existing algorithms.
Of course, if one knows in advance that there will be
several relevant contexts, the human designer (who is naturally adept at
distinguishing the appropriate context) can ‘hard-wire’ some mechanism so that
the learning algorithm can detect and make the sudden change necessary (for
example simply switching to a new neural network) to adjust to a new
context. But if one does not have such
prior knowledge then this is not possible – the appropriate contexts have to be
learnt at the same time as the content of the models. In such cases the question is “why does one need separate parts
of the model for context and content, why not just combine them into a unitary
model?”. If one does not combine them
one always has the problem of determining whether any shortcoming in the model
is due to a misidentification of context or simply erroneous content – a
problem that is impossible to solve just by looking at the context &
content of a model on its own. Rather
the tendency has often been, in the absence of a good reason to do otherwise,
to simplify things by combining the conditions of application of a model
explicitly into the model content.
This paper seeks to make some practical proposals as
to how notions of conditions of applicability and then contexts themselves can
be introduced into evolutionary computing.
Such a foray includes suggestions for principles for learning and
identifying the appropriate contexts without prior knowledge.
2.
Adding
conditions of applicability to evolving models
2.1
Standard
Evolutionary Computing Algorithms
Almost all evolutionary computing algorithms have the following basic
structure:
·
There
is a target problem;
·
There
is a population of candidate models/solutions (initially random);
·
Each
iteration some/all of the models are evaluated against the problem (either
competitively against each others or by being given a fitness score);
·
The
algorithm is such that the models which perform better at the problem are
preferentially selected for, so the worse models tend to be discarded;
·
There
is some operator which introduces variation into the population;
·
At
any particular time the model which currently performs best is the “result” of
the computation (usually taken at the end).
There are various different approaches within this,
for example, genetic programming (GP) (Koza, 1992). With GP the population of
models can have a tree structure of any shape with the nodes and terminals
taken from a fixed vocabulary. The
models are interpreted as a function or program to solve the given problem, and
usually given a numeric measure of their success at this – their
“fitness”. The models are propagated
into the next generation with a probability correlated to this fitness. The variation is provided by “crossing” the
tree structures– as shown in figure 1).
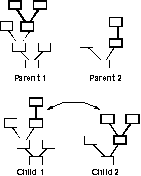
Fig. 1. The action of crossover in GP
For example, the problem may be that of finding a
functional expression, e.g. ![]() , to most closely “fit” a given set of data pairs. In this case the set of models will be trees
with terminals being either
, to most closely “fit” a given set of data pairs. In this case the set of models will be trees
with terminals being either ![]() or a set of
constants, the nodes might be the simple arithmetic operators, and the measure
of success the inverse of the error of the resulting function with respect to
the data.
or a set of
constants, the nodes might be the simple arithmetic operators, and the measure
of success the inverse of the error of the resulting function with respect to
the data.
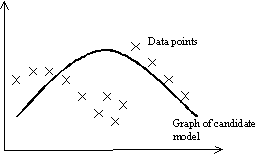
Fig. 2. An illustration of a candidate functional “fit” for some data
One of the key features of such algorithms is that
each candidate model in the population has the same scope – that of the
problem. In the long run, a model can
only be selected if it is successful (at least on average relative to other
models) over the whole domain.
Essentially the algorithm results in a single answer – the model that
generally did best. There is no
possibility that (in the long run) a model can be selected by doing well at
only a small part of the whole problem.
The technique is essentially context-free – the only context involved is
that implied by the scope of the problem and that is selected manually by the
designer.
2.2
Adding
Conditions of Application
Thus the first step is to allow each candidate model to specialise in
different parts of the problem domain. For this to be possible, success at
solving the target problem must be evaluated locally, without the model being
(unduly) penalised for not being global successful. In evolutionary terms, we allow the problem domain to be the
environment and allow different models to co-exist in different “niches” corresponding
to particular sub-spaces. This is
illustrated in fig. 3 below.
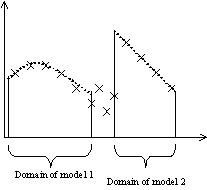
Fig. 3. Two models specialising in different parts of the problem.
It is well know that allowing “demes”, that is separate areas of evolution, acts to preserve the variety in the population. Allowing the problem space itself to structure the evolutionary should allow for clustering and competition according to what makes sense for that problem.
To do this each model in the population needs to indicate its conditions of application as well as its content, and both need to evolve in response to the problem presented within the problem domain. There are many different ways of doing this – perhaps the easiest is to simply position each model in the space and allow replication to other positions nearby.
One algorithm for this is:
Randomly generate candidate models and place them
randomly about the domain, D
for
each generation
repeat
randomly pick a point in D, P
pick n models, C, biased towards
those near P
evaluate all in C over a
neighbourhood of P
pick
random number x from [0,1)
if x < (1 – crossover
probability)
then propagate the fittest in
C to new
generation
else cross two fittest in C, put result
into
new generation
until new population is complete
next
generation
The idea is that models will propagate into the areas
of the problem domain where they are relatively successful in (until a model
that does even better locally appears).
The main parameters for this algorithm are:
·
Number
of generations;
·
Size
of population;
·
Initial
maximum depth of model;
·
Number
of models picked each tournament;
·
The
extent of the bias towards the point, P, picked;
·
The
size of the neighbourhood that the models are evaluated over;
·
Probability
of crossover.
Also, more importantly, the
following need to be specified:
·
The
problem;
·
The
language of the models in terms of their interpretation w.r.t. the problem
(usually done in terms of nodes, and terminals if this is an untyped model);
·
The
space over which the models will propagate (usually a subspace of the domain of
the problem).
A disadvantage of this technique is that once the
algorithm has finished is does not provide you with a single best answer, but
rather a whole collection of models, each with different domains of
application. If you want a complete
solution you have to analyse the results of the computation and piece together
a compound model out of several models which work in different domains – this
will not be a simple model with a neat closed form. Also there may be tough
areas of the problem where ones does not find any acceptable models at all.
Of course, these “cons” are relative – if one had used
a standard universal algorithm (that is all models having the same domain as
the problem and evaluated over that domain), then the resulting “best” model
might well not perform well over the whole domain and its form might be
correspondingly more complex as it had to deal with the whole problem at once.
2.3
An
Example Application
The example implementation I will describe is that of applying the above
algorithm to predicting the number of sunspots (shown in fig 4 below). The fitness function is the inverse of the
root mean squared error of the prediction of the model as compared to the
actual data. The models are constructed
with the nodes: PLUS, MINUS, TIMES, SAFEDIVIDE, SIN and COS,
and the terminals: x, x1,
x2, x4,
x8, x16
(which stand for the current time period and then the number of sunspots with
lags 1, 2, 4, 8, and 16 time periods respectively) the along with a random
selection of numeric constants.
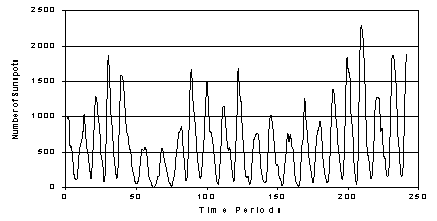
Fig. 4. The problem function – the number of sunspots
The fixed parameters were as follows:
·
Number
of generations: 50;
·
Size
of population: 723;
·
Initial
maximum depth of model: 5;
·
Number
of models picked each tournament: 6;
·
Locality
bias: 10;
·
Size
of the neighbourhood: from 1 to 7 in steps of 2;
·
Probability
of crossover: 0.1.
There were four runs, in each the neighbourhood over
which the models were tested was 1, 3, 5, and 7 respectively. The first graph (Fig. 5) shows the average fitness of the models
for these runs.
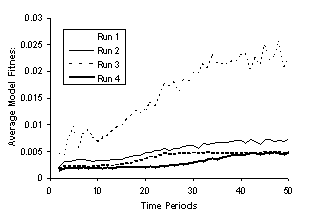
Fig. 5.
The Average Fitness of Models in the four runs
The smaller the domain the greater the average model
fitness. This is because it is much
easier to “fit” an expression to a single point than “fit” longer sections of
the graph, with fitting the whole graph being the most difficult. Of course, there is little point in fitting single
points with expressions if there is not any generalisation across the graph. After all we already have an completely
accurate set of expressions point-by-point: the original data set itself. On the other hand, if there are
distinct regions of the problem space where different solutions make sense,
being able to identify these regions and appropriate models for them would be
very useful. If the context of the whole problem domain is sufficiently
restricted (which is likely for most of the “test” or “toy” problems these
techniques are tried upon).
Figure 6, below, shows the
maximum coverage of the models for the four runs. In each case early on a few models take over from the others in
terms of the amount of problem space they occupy. Then as they produce descendants with variations, these
descendants compete with them for problem space and the coverage of any
particular model equals out.
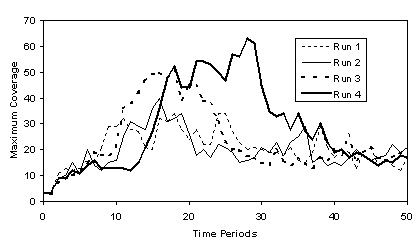
Fig 6.
Maximum coverage (in terms of number of positions) of models over the four runs
One individual propagates itself for a while before
new models (often its own offspring) start to compete with it. This is illustrated in Fig. 7. Which shows
the coverage of the dominant model at each stage of run four, where the
different individual models are identified.
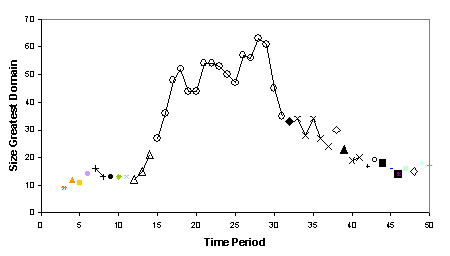
Fig 7.
Maximum coverage of individual models in fun 4 (the same individual is
indicated by the same symbol and are connected)
Thus you get a short-term domination by individual
models by propagation and a longer-term effect composed of the domination of
closely related but different individuals – what might be called
“species”. The end of run 4 is analysed
below using a very rough division into such species. Those models that start with the same 25 characters are
arbitrarily classed as the same species.
The 10 most dominant species at the end of run 4 are shown below in
Table 1.
|
Species |
Start
of model |
Size of Domain |
|
1 |
[ MINUS [
SAFEDIVIDE [ PLUS … |
260 |
|
2 |
[ PLUS [ PLUS
[ SIN [ TIMES … |
187 |
|
3 |
[ PLUS [
SAFEDIVIDE [ PLUS … |
31 |
|
4 |
[ MINUS [
MINUS [ x1] [ TIME ... |
24 |
|
5 |
[ PLUS [ x1] [
SIN [ PLUS [ T … |
22 |
|
6 |
[ PLUS [ MINUS
[ x1] [ 0.641 ... |
19 |
|
7 |
[ PLUS [ MINUS
[ x1] [ 0.868 … |
17 |
|
8 |
[ SAFEDIVIDE [
PLUS [ x1] [ … |
13 |
|
9 |
[ MINUS [
MINUS [ x1] [ 0.57 … |
12 |
|
10 |
[ PLUS [ PLUS
[ SIN [ 0.5712 … |
9 |
Table 1. The 10 “species” with the largest domain
As you can see two quite different such “species” dominate. The figure below (Fig. 8.) Indicates the domains of these species.

Fig. 8. The
domains of the ten most common species (most dominant in the top line) of
models at the end of run 4
Simply by inspection, some of these species do seem to
have identifiable parts of the problem space in which they apply. This effect could be accentuated by adding a
period of “consolidation” at the tail end of the algorithm. During this period there would be no
crossover and the locality of the operation of the propagation process kept to
a minimum. This would allow individual
models to have a chance to “dominate” contiguous sub-spaces of the whole
domain. Such a consolidation period has obvious parallels with the technique of
“simulated annealing”, and I guess a similar technique of slowly lowering the
“temperature” (the distance models can jump around) of the algorithm towards
the end might have similar effects.
3.
The
move to really learning and using contexts
Given the picture of “context”
as an abstraction of the background inputs to a model, implicit in the transfer
of knowledge from learning to application (that I argued for in Edmonds,
1999). There is still a step to take in
order for it to be truly “context” that is being utilised – a collection of
conditions of application become a context if it is sensible to abstract them
as a coherent unit. Now it may be
possible for a human to analyse the results of the evolutionary algorithms just
described and identify context – these would correspond to niches in the
problem domain that a set of models competes to exploit – but the above
algorithm itself
does not do this.
Rather the identification of context in a problem
reveals something about the problem itself – it indicates that there are
recognisable and distinct sub-cases where different sets of
models/rules/solutions apply. In other
words that there is a sufficient clustering or grouping of the conditions
of applications of relevant models that it makes sense to abstract from this
set of domains to a context.
This is what a biologist does when identifying the “niche” of an
organism (or group of organisms) – this is not highly detailed list of where
this organism happened to live, but a relevant abstraction from this taking
into account the way the organism survives.
This idea of abstracting a context from clusters of model domains is
illustrated in Fig. 9. below.
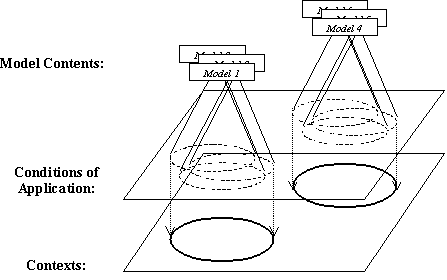
Fig. 9.
Contexts abstracted from models with different, but clustered, domains
of application
Of course, it is not necessarily the case that the
model domains will be clustered so that it is at all sensible to abstract
them into explicit contexts. Rather
this is a contingent property of the problem and the strategy, resources and
limitations of the learner. The
existence of meaningful contexts arises out of the fact that there
happen to
be heuristics that can do this clustering, otherwise even if all the
relevant models are not universal in scope context, as such, might not arise.
Such an abstraction requires a further level of
learning not present in the above algorithm.
Extra levels of learning require resources and so must be justified – so
why would one need to cluster and identify contexts rather than directly manipulate
the model domains themselves? In the
natural world organisms do not usually bother to explicitly identify where they
live. A simple answer is that an
abstracted context is a far more compact and elegant representation of the
conditions under which a whole collection of models might hold, but this is not
a complete answer because the overhead in retaining the detail of the source
models domains may not be an advantage compared to the advantage of knowing exactly
when a model applies. A partial answer
to this question will be offered in the next section.
4.
Knowing
whether it is the context or the content that is wrong
There is a fundamental difficulty is in attributing the source of error
displayed by a model. Perhaps this,
more than anything else, characterises different strategies for learning. Given that a model displays an unacceptable
level of error in a situation, what are the options? They include:
1.
Changing
the model content (either by a minor elaboration or parameter adjustment or by
a more radical restructuring);
2.
Adjusting
the conditions of application so as to exclude the domain where the model did
not work;
3.
Making
the predictions of the model less precise so as to allow for the error;
4.
Finally,
and most radically it may be necessary to change the language/basis of the
model formulation itself.
The problem is to determine which is appropriate in each case. In this paper I am particularly focusing of the decision between (1) and (2) above (for a wider discussion see Moss and Edmonds 1998).
The point is that in isolation there is no principled way of telling whether it is the model content or context that is wrong. However, given that the problem or circumstances is such that there are meaningful clusterings of the domains of models into contexts there is a way, namely: to check the predictions of other models with the same context. If other models associated with the same context are also in error, then it is probably the context that is wrong; if the other models associated with the same context are correct then it is most likely the original model content that is in error. This collective view of model building suggests the following principles of context identification:
1. (Formation) A cluster of models with similar or closely related domains suggests these domains can be meaningfully abstracted to a context.
2. (Abstraction) If two (or more) contexts share a lot of models with the same domain, they may be abstracted (with those shared models) to another context. In other words, by dropping a few models from each allows the creation of a super-context with a wider domain of application.
3. (Specialisation) If making the domain of a context much more specific allows the inclusion of many more models (and hence useful inferences) create a sub-context.
4. (Content Correction) If one (or only a few) models in the same context are in error whilst the others are still correct, then these models should either be removed from this context or their contents altered so that they give correct outputs (dependent on the extent of modifications needed to “correct” them)
5. (Content Addition) If a model has the same domain as an existing context, then add it to that context.
6. (Context Restriction) If all (or most) the models in a context seem to be simultaneously in error, then the context needs to be restricted to exclude the conditions under which the errors occurred.
7. (Context Expansion) If all (or most) of the models in a context seem to work under some new conditions, then expands the context to include these conditions.
8. (Context Removal) If a context has only a few models left (due to principle 2) or its domain is null (i.e. it is not applicable) forget that context.
These conditions are somewhat circular – context are
guessed at from clusterings of model domains, and model contents are changed in
models who disagree with a majority of models in the same context. However, I do think that these principles
should allow the “bootstrapping” of meaningful contexts. A starting point for this process can be the
assumption that models learnt in similar circumstances (situations) share the
same context – that the relevant contexts are defined by the similarity of
experience. Later these assumption
based contexts can be abstracted, refined and corrected using the above. Any bootstrapping learning process depends
upon the possibility of starting with simple models and situations and working
upwards (compare Elman 1993).
5.
Related
Work
5.1
Evolutionary
Computation
The obvious technique from evolutionary computation which employs ideas
of model domains are Holland’s “Classifier” (Holland 1992) and descendent
techniques. Here each model is
explicitly divided into the conditions and action of a model. Such models are not designed to evolve in
parallel as in the above algorithm, but to form computational chains.
Eric Baum has developed this idea by applying more
rigorous property rules to govern the chaining of models and the apportionment
of reward. Thus in his model each model
has an implicit domain, in that it is only applies when it out-bids other
models in order to be applied (Baum and Durdanovic, 2000b). In the most recent version of his algorithm
(called Hayek 4) he also introduces explicit conditions of application as each
model is a Post production rule (Baum and Durdanovic, 2000a).
5.2
Machine
Learning
There has been more attention to context-related ideas in the effort to
improve inductive and neural network learning techniques. Some techniques
require the explicit identification of what the contextual factors will be and
then augment the existing machine learning strategy with a meta-level algorithm
utilising this information (e.g. Turney 1993 or Widmer 1997). Others look to augment strategies using
implicit information about the context to adjust features of the learning such as the weightings (Aha 1989), or
normalisation (Turney and Halasz 1993).
These usually utilise a clustering algorithm and thus are closest to the
evolutionary technique I have described (e.g. Aha 1989).
Peter Turney surveys the various heuristics tried to mitigate the effects of context on machine learning techniques in (Turney 1996). He keeps an extensive bibliography on context-sensitive learning at URL:
6.
Conclusion
If one abandons the myopic view of focusing on single model solutions and
models, and looks at their group dynamics instead, then further
learning heuristics become available.
These allow one to distinguish when it is the identification of the
content or the context that is at error.
Indeed it is only by considering groups of models that contexts themselves
make any sense.
7.
References
Aha, D. W.
(1989). Incremental, instance-based learning of independent and graded concept
descriptions. In Proc. of the 6th Int. Workshop on Machine Learning,
387-391. CA: Morgan Kaufmann.
Baum, E. and
Durdanovic, I. (2000a). An Evolutionary Post-Production System. http://www.neci.nj.nec.com/homepages/eric/ptech.ps
Baum, E. and
Durdanovic, I. (2000b). Evolution of Co-operative Problem Solving. http://www.neci.nj.nec.com/homepages/eric/hayek32000.ps
Edmonds, B.
(1990). The Pragmatic Roots of Context. CONTEXT'99, Trento, Italy, September
1999. Lecture
Notes in Artificial Intelligence, 1688:119-132. http://www.cpm.mmu.ac.uk/cpmrep52.html
Elman, J. L.
(1993). Learning and Development in Neural Networks - The Importance of
Starting Small. Cognition, 48:71-99.
Gigerenzer, G
and Goldstein, D. G. (1996). Reasoning the fast and frugal way: Models of
bounded rationality. Psychological Review, 104:650-669.
Harries, M.
B., Sammut, C. and Horn, K. (1998). Extracting Hidden Contexts. Machine
Learning, 32:101-126.
Holland, J. H.
(1992). Adaptation
in Natural and Artificial Systems, 2nd Ed., MIT Press,
Cambridge, MA.
Koza, J. R.
1992. Genetic
Programming: On the Programming of Computers by Means of Natural Selection.
Cambridge, MA: MIT Press.
Moss, S. and
Edmonds, B. (1998). Modelling Economic Learning as Modelling. Cybernetics
and Systems, 29:215-248. http://www.cpm.mmu.ac.uk/cpmrep03.html
Turney, P. D.
(1993). Exploiting context when learning to classify. In Proceedings of the European Conference
on Machine Learning, ECML-93. 402-407. Vienna: Springer-Verlag.
Turney, P. D.
(1996). The management of context-sensitive features: A review of strategies. Proceedings
of the ICML-96 Workshop on Learning in Context-Sensitive Domains,
Bari, Italy, July 3, 60-66.
Turney, P. D.
and Halasz, M. (1993). Contextual normalisation applied to aircraft gas turbine
engine diagnosis. Journal of Applied Intelligence, 3:109-129.
Widmer, G.
(1997). Tracking Context Changes through Meta-Learning. Machine Learning, 27:259-286.