THE ADAPTIVE ADVANTAGE OF SYMBOLIC THEFT OVER SENSORIMOTOR TOIL: GROUNDING
LANGUAGE IN PERCEPTUAL CATEGORIES
1. Language Evolution: A Martian Perspective
Whatever
the adaptive advantage of language was, it was indisputably triumphant. If all
our linguistic capabilities were subtracted from the repertoire of our species today,
very little would be left. Not only would all the fruits of science, technology
and culture vanish, but our development and socialization would be arrested at
the stage still occupied currently by the members of all other species, along
with only the severely retarded members of our own. Buried somewhere among all
those undeniable benefits that we would lose if we lost language there must be
a clue to what language’s original bonus was, the competitive edge that set us
inexorably on our unique evolutionary path, distinct from all the nonspeaking
species (Harnad, Steklis & Lancaster 1976; Steels 1997).
There has
been no scarcity of conjectures as to what that competitive edge might have
been: It helped us hunt; it helped us make tools; it helped us socialize. There
is undoubtedly some merit in such speculations, but it is hard to imagine how
to test them. Language is famously silent in the archeological and
paleontological record, requiring interpreters to speak for it; but it is the
validity of those very interpretations that is at issue here.
Perhaps we
need to take a step back, and look at our linguistic capacity from the
proverbial Martian anthropologist's perspective: Human beings clearly become
capable of doing many things in their world, and from what they can do, it can also be inferred that they know
a lot about that world. Without too much loss of generality, the Martian could
describe that knowledge as being about the kinds of things there are in the
world, and what to do with them. In other words, the knowledge is knowledge of categories: objects, events, states,
properties and actions.
Where do
those categories come from? A Martian anthropologist with a sufficiently
long-range database could not fail to notice that some of our categories we
already have at birth or soon after, whereas others we acquire through our
interactions with the world (Harnad, 1976). By analogy with the concept of
wealth, the Martian might describe the categories acquired through the efforts
of a lifetime to be those that are earned
through honest toil, whereas those that we are born with and hence not
required to earn he might be tempted to regard as ill-gotten gains -- unless
his database was really very long-range, in which case he would notice that
even our inborn categories had to be earned through honest toil: not our own
individual toil, nor even that of our ancestors, but that of a more
complicated, collective phenomenon that our (ingenious) Martian anthropologist
might want to call evolution.
So,
relieved that none of our categories were acquired other than through honest
toil, our Martian might take a close look at precisely what we had done to earn
those that we did not inherit. He would find that the way we earned our
categories was through laborious, real-time trial and error, guided by
corrective feedback from the consequences of sorting things correctly or
incorrectly (Catania & Harnad, 1988). As in many cases the basis for
sorting things correctly was far from obvious, he would note that our honest toil
was underwritten by a substantial inborn gift, that of eventually being able to
find the basis for sorting things correctly, somehow. A brilliant cognitive
theorist, our Martian would immediately deduce that in our heads there must be
a very powerful device for learning to detect those critical features of things
(as projected onto our sensory surfaces) on the basis of which they can be
categorized correctly (Harnad, 1996b). Hence he would not be surprised that
this laborious process takes time and effort -- time and effort he would call
"acquiring categories by Sensorimotor
Toil" (henceforth Toil).
Our Martian
moralist would be surprised, however, indeed shocked, that the vast majority of
our categories turn out not to be learned
by Toil after all, even after discounting the ones we are born with. At first
the Martian thinks that these unearned categories simply appear spontaneously;
but upon closer inspection of his data he deduces that we must in fact be stealing them from one another somehow.
For whenever there is evidence that one of us has acquired a new category
without first having performed the prerequisite hours, weeks or years of Toil,
in the laborious real-time cycle of trial, error and feedback, there is always
a relatively brief vocal episode between that individual and another one who
has himself either previously earned that category through sensorimotor Toil,
or has had a very brief vocal encounter with yet another individual who has
himself either… and so on.
Without
blinking, our Martian dubs this violation of his own planet's Protestant work
ethic "the acquisition of categories by Theft," and immediately begins to search for the damage done
to the victims of this heinous epistemic crime. To his surprise, however, he
finds that (except in very rare cases, dubbed "plagiarism," in which
the thief falsely claims to have acquired the stolen category through his own
honest toil), category Theft seems to be largely a victimless crime.
Ever the
brilliant cognitive theorist, our Martian would quickly discern that the
mechanism underlying Theft must be related to the one underlying Toil, and that
in principle it was all quite simple. The clue was in the vocal episode: All
earthlings start with an initial repertoire of categories acquired by
sensorimotor Toil (supplemented by some inborn ones); these categories are
grounded by the internal mechanism that learns to detect their distinguishing
features from their sensorimotor projections. These grounded categories are then assigned an arbitrary symbolic name
(lately a vocal one, but long ago a gestural one, his database tells him
[Steklis & Harnad, 1976]). This name resembles neither the members of the
category, nor their features, nor is it part of any instrumental action that
one might perform on the members of the category. It is an arbitrary symbol, of a kind with which our Martian theorist is
already quite familiar with, from his knowledge of the eternal Platonic truths
of logic and mathematics, valid everywhere in the Universe, which can all be
encoded in formal symbolic notation (Harnad, 1990).
When our
Martian analyses more closely the brief vocal interactions that always seem to
mediate Theft, he finds that they can always be construed in the form of a proposition that has been heard by the
thief. A proposition is just a series of symbols that can be interpreted as
making a claim that can be either true or false. The Martian knows that
propositions can always be interpreted as statements about category membership.
He quickly deduces that propositions make it possible to acquire new categories
in the form of recombinations of old ones, as long as all the symbols for the
old categories are already grounded in Toil (individual or evolutionary). He
accordingly conjectures that the adaptive advantage of language is specifically
the advantage of Symbolic Theft over Sensorimotor Toil, a victimless crime that
allows knowledge to be acquired without the risks or costs of direct trial and
error experience.
Can the
adaptive advantage of Symbolic Theft over Sensorimotor Toil be demonstrated
without the benefit of the Martian Anthropologist's evolutionary database (in
which he can review at leisure the videotape of the real-time origins of
language)? We will try to demonstrate them in a computer simulated toy world considerably more impoverished
than the one studied by the Martian. It will be a world consisting of mushrooms
and mushroom foragers who must learn what to do with which kind of mushroom in
order to survive and reproduce (Parisi, Cecconi & Nolfi, 1990; Cangelosi
& Parisi, 1998). This
artificial-life approach to modeling language evolution has itself evolved
appreciably in the last decade (Cangelosi & Parisi, 2002; Kirby, 2000;
Steels, 1997;) and is based on languages whose terms are grounded in the
objects in the simulated world (Steels, 2002; Cangelosi, 2001; Steels &
Kaplan, 1999).
Before we
describe the simulation we must introduce some theoretical considerations that
are too fallible to be attributed to our Martian theorist: One concerns a
fundamental limitation on the acquisition of categories by Symbolic Theft (the
symbol grounding problem) and the other concerns the mechanism underlying the
acquisition of categories by Sensorimotor Toil (categorical perception).
1.1. The Symbol Grounding Problem
Just as the
values of the tokens in a currency system cannot be based on still further
tokens of currency in the system, on pain of infinite regress -- needing
instead to be grounded in something like a gold standard or some other material
resource that has face-value -- so the meanings of the tokens in a symbol
system cannot be based on just further symbol-tokens in the system. This is
called the symbol grounding problem (Harnad, 1990). Our candidate for the
face-valid groundwork of meaning is perceptual
categories. The meanings of symbols can always be cashed into further
symbols, but ultimately they must be cashed into something in the world that
the symbols denote. Whatever it is inside a symbol system that allows it to
pick out the things its symbols are about, on the basis of sensorimotor
interactions with them (Harnad, 1992; 1995), will ground those symbols; those
grounded symbols can then be combined and recombined in higher-level symbolic
transactions that inherit the meanings of the ground-level symbols. A simple
example is "zebra," a higher-level symbol that can inherit its
meaning from the symbols "striped" and "horse," provided
"striped" and "horse" are either ground-level symbols, or
grounded recursively in ground-level symbols by this same means (Harnad 1996a;
Cangelosi, Greco & Harnad, 2001).
The key to
this hierarchical system of inheritance is the fact that most if not all
symbolic expressions can be construed as propositions about set (i.e.,
category) membership. Our Martian had immediately intuited this: The simplest
proposition "P," which merely asserts that the truth-value of P is
true, is asserting that P belongs to the set of true propositions and not the
set of false propositions. In the classical syllogism: "All men are
Mortal. Socrates is a Man. Therefore Socrates is Mortal," it is again
transparent that these are all propositions about category membership. It
requires only a little more reflection to construe all the sentences in this
paragraph in the same way, and even to redraw them as Venn Diagrams depicting
set membership and set inclusion. Perceptual categories are the gold standard for this network of
abstractions that leads, bottom-up, from "horse," "striped"
and "zebra" all the way to "goodness," "truth"
and "beauty."
1.2. Categorical Perception
Can
perceptual categories bear the weight of grounding an entire symbolic edifice
of abstraction? Some parts of the world that our senses must categorize and tag
with a symbolic name do obligingly sort themselves into disjunct, discrete
categories that admit of no overlap or confusion, so our senses can duly detect
and distinguish them. For these happy categories it does look as if the
perceptual groundwork can bear the burden. But in those parts of the world
where there is anything approaching the "blooming, buzzing confusion"
that William James wrote about, the world alone, and passive senses (or even
active, moving, Gibsonian ones; Gibson, 1979) are not enough. Here even an
active sensorimotor system needs help in detecting the invariants in the sensorimotor interaction with the world that afford the ability to sort the subtler,
more confusable things into their proper categories. Neural networks are
natural candidates for the mechanism that can learn to detect the invariants in
the sensorimotor flux that will eventually allow things to be sorted correctly
(Harnad, 1992; 1993). This is the process we have agreed to call Toil.
A
sensorimotor system with human-scale category learning capacities must be a plastic (modifiable) one: Inside the
system, the internal representations of categories must be able to change in
such a way as to sort themselves, reliably and correctly. It is perhaps an
oversimplification to think of these internal representations as being embedded
in a great, multidimensional similarity
space, in which things position themselves in terms of their distances from
one another, but this simplification is behind the many regularities that have been
revealed by the psychophysical method of multidimensional scaling (Livingston
& Andrews, 1995) which has been applied to category learning and
representation in human subjects (Andrews, Livingston & Harnad, 1998). What
has been found is that during the course of category learning by what we have
called sensorimotor Toil, the structure of internal similarity space changes in
such a way as to compress the
perceived differences between members of the same category and expand the differences between members
of different categories, with the effect of separating categories in similarity
space that were highly interconfusable prior to the Toil (Andrews, Livingston
& Harnad, 1998; Goldstone, 1994; Pevtzow & Harnad, 1997). This
compression/separation in turn allows an all-or-none (categorical) boundary to be placed between the regions of
similarity space occupied by members of different categories, thereby allowing
them to be assigned distinct symbolic names.
These
compression/separation effect has come to be called categorical perception (CP) (Harnad 1987) and has been observed
with both inborn categories and learnt ones, in human subjects (Goldstone,
1994; Pevtzow & Harnad, 1997) as well as in animals and in neural nets
(Cangelosi, Greco & Harnad, 2001; Harnad, Hanson & Lubin 1991; 1995; Nakisa & Plunkett, 1998; Tijsseling
& Harnad, 1997). The neural nets offer the advantage that they give us an
idea of what the functional role of CP might be, and what they suggest is that
CP occurs in the service of categorization. It can be seen, for example, as
changes in the receptive fields of
hidden units in the supervised backpropagation nets that will be used in this
study. What will be analyzed for the first time here is how the CP
"warping" of similarity space that occurs when categories are
acquired by sensorimotor Toil is transferred and further warped when categories
are acquired by Theft. Categorical perception induced by language can thus be
seen as an instance of the Whorfian Hypothesis (Whorf 1964), according to which
our language influences the way the world looks to us.
2. The
Mushroom World
Our
simulations take place in a mushroom
world (Cangelosi & Parisi, 1998; Harnad, 1987) in which little virtual organisms forage among the mushrooms, learning
what to do with them (eat or don't eat, mark or don't mark, return or don't
return). The foragers feed, reproduce and die. They must learn that
mushrooms with feature A (i.e. those with black spots on their tops, as
illustrated in Figure 1) are to be eaten; mushrooms with feature B (i.e. a dark
stalk) are to have their location marked, and mushrooms with both features A
and B (i.e. both black-spotted top and dark stalk) are to be eaten, marked and
returned to. All mushrooms also have three irrelevant features, C, D and E,
which the foragers must learn to ignore.
Apart from
being able to move around in the environment and to learn to categorize the
mushrooms they encounter, the foragers also have the ability to vocalize. When
they approach a mushroom, they (innately)
emit a call associated with what they are about to do to that mushroom
(EAT, MARK). The correct action pattern
(eat, mark), coupled (innately) with the correct call (EAT, MARK) are
learned during the foragers' lifetime through supervised learning (Sensorimotor
Toil). Under some conditions, the foragers also receive as input, over and
above the features of the mushroom itself (+/-A, +/-B, +/-C, +/-D, +/-E), the
call of another forager. This will be used to test the adaptive role of the Theft
strategy. Note, however, that in the present simulations the thief steals only the knowledge, not the
mushroom (cf. note 1 for simulations on
environments with shared resources).
The
foragers' world is a 2-dimensional (2D) grid of 400 cells (20x20). The
environment contains 40 randomly located mushrooms, 10 per category. Mushrooms are grouped in four categories
according to the presence/absence of features A and B: 00, A0, 0B, and AB
(Figure 1). In each world there are 40 mushrooms: 10 instances of each of the
four categories. Our ecological interpretation
of the marking behavior is that
it has two functions: Both the inedible 0B and the edible AB mushrooms have a
toxin that is painful when inhaled, but digging into the earth (marking) immediately after exposure
blocks all negative effects. There is also a delayed contingency on the AB
mushrooms only, which is that wherever they appear, many more mushrooms of the
same kind will soon grow in their place. So with AB mushrooms it is adaptive to
remember to return to the marked spots.
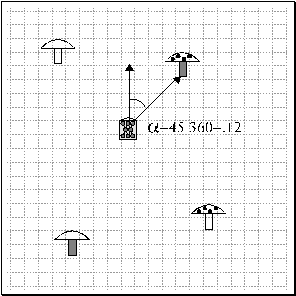
Figure 1: 2D world with one forager and the four samples of mushrooms. Mushroom feature A is the presence of black dots on the top; feature B is a dark stalk. Mushroom position corresponds to the normalized relative angle between forager's orientation and the closest mushroom.
Feature A
is the black-spotted top and feature B is the dark stalk. Mushroom position is
encoded as the normalized relative angle between the direction the forager is
facing and the direction of the closest mushroom. In this simulation, the
foraging is done by only one forager at a time. As it moves, the forager
perceives only the closest mushroom. For each mushroom, the input to the
forager consists of the 5 +/- features plus its location relative to the
forager, expressed as the angle a, between its position and the direction the forager is facing. The
angle is then normalized to the interval [0, 1]. The five visual features A, B,
C, D, E are encoded in a binary localist representation consisting of five
units each of which encodes the presence/absence of one feature. An A0 mushroom
would be encoded as 10***, with 1 standing for the presence of feature A, 0 for
the absence of feature B and *** being either 0 or 1 for the 3 irrelevant
features, C, D, and E. 0B mushrooms are encoded as 01***, and AB as 11***. The
calls that can be produced in the presence of the mushroom are also encoded in
a localist binary system. There are 3 units for each of the three calls: 1**
EAT, *1* MARK and **1 RETURN, so EAT+MARK+RETURN would be 111. Like the Calls,
the three actions of eating, marking and returning are encoded with localist
units.
3. The
Neural Network and Genetic Algorithm
The
forager's neural network processes the sensory information about the closest
mushroom and activates the output units corresponding to the movement, action
and call patterns. The net has a feedforward architecture (Figure 2) with 8
input, 5 hidden and 8 output units. The first input unit encodes the angle to
the closest mushroom. Five input units encode the visual features and three
input units encode incoming calls (if any). Two output units encode the four
possible movements (one step forward, turn 90 degrees right, turn 90 degrees
left, or stay in place) in binary. Three action units encode the action
patterns eat, mark, and return, and three call units encode the corresponding
three calls, EAT, MARK, and RETURN.
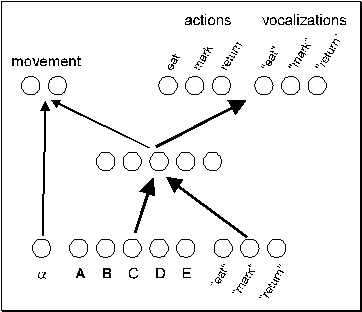
Figure 2 - Neural network architecture.
A forager's lifetime lasts for 2000 actions (100 actions in 20 epochs).
Each epoch consists of sampling a different distribution of 40 mushrooms. Each
action consists of two spreads of activation in the neural network, one for the
action (movement and action/call) and one for an imitation task. The forager
first produces a movement and an action/call output using the input information
from the physical features of the mushroom. The forager's neural network then
undergoes a cycle of learning based on the backpropagation algorithm
(Rumelhart, Hinton & Williams, 1986).
The net's
action and call outputs are compared with what they should have been; this
difference is then backpropagated so as to weaken incorrect connections and
strengthen correct ones. In this way the forager learns to categorize the
mushrooms by performing the correct action and call. In the second spread of
activation the forager also learns to imitate the call. It receives as input
only the correct call for that kind of mushroom, which it must imitate in its
call output units. This learning is likewise supervised by backpropagation.
The
population of foragers is also subject to selection and reproduction as
generated by the genetic algorithm (Goldberg, 1989). The population size is 100
foragers and remains constant across generations. The initial population
consists of 100 neural nets with a random weight matrix. During the forager's
lifetime its individual fitness is computed according to a formula that assigns
points for each time a forager reaches a mushroom and performs the right action
on it (eat/mark/return) according to features A and B. At the beginning of its
life, a forager does not become much fitter from the first mushrooms it
encounters because it takes some time to learn to categorize them correctly. As
errors decrease, the forager's fitness increases. At the end of their
life-cycles, the 20 foragers with the highest fitness in each generation are
selected and allowed to reproduce by engendering 5 offspring each. The new
population of 100 (20x5) newborns is subject to random mutation of their
initial connection weights for the motor behavior, as well as for the actions
and calls (thick arrows in Figure 2); in other words, there is neither any
Lamarckian inheritance of learned weights nor any Baldwinian evolution of
initial weights to set them closer to the final stage of the learning of 00,
A0, 0B and AB categories. This selection cycle is repeated until the final
generation.
4. Grounding
Eat and Mark Directly Through Toil
Two
experimental conditions were compared: Toil and Theft. Foragers live for two life-stages
of 2000 actions each. The first life-stage is identical for both populations:
they all learn, through sensorimotor Toil, to eat mushrooms with feature A and
to mark mushrooms with feature B. (AB mushrooms are accordingly both eaten and
marked.) Return is not taught during the first life-stage. The input is always
the mushroom's position and features, as shown in Table 1. In the second
life-stage, foragers in the Toil condition go on to learn to return to AB
mushrooms in the same way they had learned to eat and mark them through honest
toil: trial and error supervised by the consequences of returning or not
returning (Catania & Harnad 1988). In contrast, foragers in the Theft
condition learn to return on the basis of hearing the vocalization of the
mushrooms' names.
Table 1 - Input and backpropagation for Toil and Theft
learning and for imitation learning
|
Condition |
Feature Input |
Call Input |
Behavior Backprop |
Call Backprop |
|
TOIL EAT-MARK |
YES |
NO |
YES |
YES |
|
TOIL RETURN |
YES |
NO |
YES |
YES |
|
THEFT RETURN |
NO |
YES |
YES |
YES |
|
IMITATION |
NO |
YES |
NO |
YES |
We ran ten
replications for each of the two conditions. In the first 200 generations, the foragers
only live for the first life-stage. From generation 200 to generation 210 they
live on for a second life-stage and must learn the return behavior. The first
200 generations are necessary to evolve and stabilize the ability to explore
the world and to approach mushrooms. After the foragers are able to move in the
2D environment and to approach mushrooms, they learn the basic categories plus
their names, EAT and MARK. The average fitness of the ten replications is shown
in Figure 3. The populations that evolve in these 10 runs are the same ones
that are then used in the Toil and Theft conditions from generations 200 to
210.
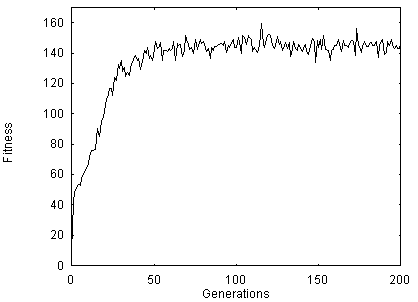
Figure 3 - Average fitness of the best 20 individuals in ten replications. Foragers lived one life-stage and only eating and marking was taught.
In the next
runs, the second life-stage differs for the Toil and Theft groups: The Toil
group learns to return and to vocalize RETURN on the basis of the feature input
alone, as in the previous life-stage. Their input and supervision conditions
are shown in Table 1. In the Theft condition the foragers rely on other
foragers' calls to learn to return. They do not receive the feature input, only
the vocalization input.
Our
hypothesis is that the Theft strategy is more adaptive (i.e. results in greater
fitness and more mushroom collection) than the Toil strategy. To test this, we
compare foragers' behavior for the two conditions statistically. For our
purposes we count the number of AB mushrooms that are correctly returned to.
The average of the best 20 foragers in all 10 replications is 54.7 AB mushrooms
for Theft and 44.1 for Toil. That is, Thieves successfully return to more AB
mushrooms than do Toilers. This means that learning to return from the grounded
names EAT and MARK is more adaptive than learning it through direct toil based
on sampling the physical features of the mushrooms. To compare the two
conditions, we performed a repeated measures analysis of variance (MANOVA) on
the 10 seeds. The dependent variables were the number of AB mushrooms collected
at generation 210 averaged over the 20 fittest individuals in all 10
generations. The independent variable was Theft vs. Toil. The difference
between the two conditions was significant [F(1,9)=136.7 p<0.0001]. Means
and standard deviations are shown in Figure 4.
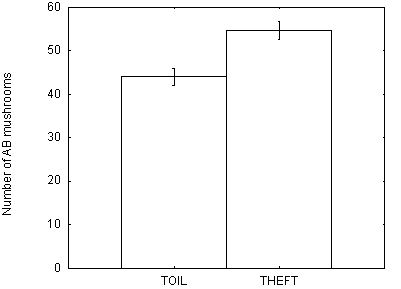
Figure 4 - Mean number of AB mushrooms correctly returned to in Toil and Theft simulations
5. Theft vs
Toil: Simulating Direct Competition
A direct way
to study the adaptive advantage of Theft over Toil is to see how they fare in
competition against one another. We ran
10 competitive simulations, using the genotypes of generation 200 from the
previous 10 runs. From generation 201 to 220, the 100 foragers of each
population are randomly divided into 50 Thieves and 50 Toilers for the learning
to return. There is no real on-line competition in our simulations
because in each run, only one individual is tested in its world. The number of
AB mushrooms to which a forager is able to return will strongly affect its
fitness. Direct competition occurs only at the end of the life cycle, in the
selection of the fittest 20 to reproduce. Direct competition for variable mushroom resources in shared
environments has been studied separately in other simulations (note 1);
in the present ecology, the assumption is that mushrooms are abundant and that
the only fitness challenge is to emerge among the top 20 eaters/markers of the
generation. Figure 5 shows the proportion of Thieves in the overall population
of the 10 replications of Theft vs Toil (from generation 200 to 220). Even
though Thieves are only 50% of the population at generation 201, they gradually
come to outnumber Toilers, so that in less than 10 generations the whole
population consists of Thieves.
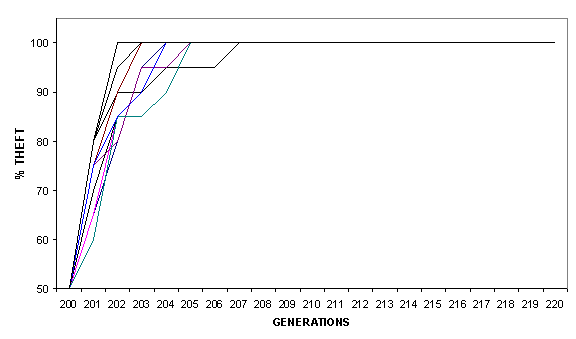
Figure 5 - Percentage of Thieves in the 10 competitive simulations.
6. What
Changes During Learning? Analysis of Internal Representations
In this
section we compare the changes in the foragers' hidden-unit representations for
the mushrooms to determine what it is that changes
internally during Toil and Theft. The activations of the 5 hidden units are
recorded during a test cycle in which the forager is exposed to all the
mushrooms as input. We will report the analysis of a single case study using
the network of the fittest individual in seed 8. These results are
representative of the learning dynamics in all nets that successfully learned
to categorize mushrooms.
We first
used Principal Components Analysis (PCA) to display the network's internal
states in two dimensions, thereby reducing the 5 activations to 2 factor
scores. PCA, however, has the limitation that the different conditions cannot
be compared directly because of differences in scale. For each PCA, factor
scores are normalized to a distribution with a mean of 0 and a standard
deviation of 1. Hence this analysis can only be used to compare internal
representations within each condition, not between conditions.
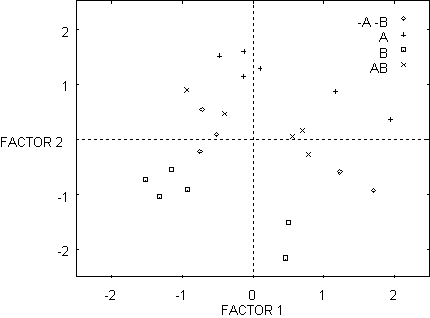
Figure 6 - Similarity space for network with random weights. Factors are obtained after PCA on the activation values of the five hidden units.
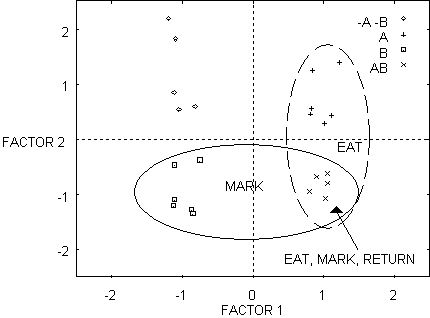
Figure 7 - Similarity space for network that learned to eat, mark, and return by Toil.
Figure 6
and 7 show the effect of category learning (Toil) on the distances between the
internal representations of the mushrooms in hidden unit similarity space. In
Figure 6, prior to Toil, the four kinds of mushroom are not clearly
distinguishable. During the course of learning the actions/calls eat-mark-return,
the representations form four separable clusters. We will now show how these
representations can be used to analyze the effects of Toil and Theft learning
on similarity space directly.
7. Categorical
Perception Effects
The change in
our networks' hidden-unit representations during the course of category
learning can be analyzed and understood in terms of learned categorical
perception (CP) effects (Harnad 1987, Goldstone 1994; Andrews et al., 1998),
i.e. the compression of within-category distances and the expansion of
between-category distances. CP has already been demonstrated to occur with Toil
learning (Harnad et al., 1991; 1995; Goldstone et al., 1996; Csato et al.,
submitted); we will now extend this to an examination of what happens to the
internal representations with Theft learning.
To overcome
the limitations of the previous principal component analysis, we record the
Euclidean distances between and within categories using the
coordinates of the five hidden unit activations directly. At the end of each
simulation, the 5 fittest foragers in each population are tested by giving them
40-mushroom samples as input. The hidden unit activations for each kind of
mushroom are saved for three input conditions: (1) Features-only (only the
5-bit feature input); (2) Calls-only (only the 3-bit call input) and (3)
Features+Calls (both types of input). The within-category distances are
calculated as the mean squared Euclidean distances between each individual
mushroom's coordinates and its category mean. There are four means, one for 00,
A0, 0B, and AB respectively. These
parameters reflect the within-category similarity amongst the members of each
category: the lower the average within-category distance for a category, the
more similar the hidden-unit representations of its members. Between-category
distances are calculated as the distances between the category means. These
reflect the dissimilarity between the members of different categories: the
higher the average between-category distance for a pair of categories, the
greater the difference between the hidden-unit representations of their
respective members.
Four
learning conditions are used to analyze within-category and between-category
distances for CP effects: (1) Pre-learning,
for random-weight nets before learning; (2) No-return,
for nets that were only taught to eat and to call EAT, and to mark and to call
MARK, (3) Toil, for nets that also
learned to return and to call RETURN with feature input, (4) and Theft for learning to return from calls
alone. In every replication one mean was obtained for each of the 10 between-
and within-category distances (4 within measures for each category, plus 6
between measures for all the possible pairings of the 4 categories) by
averaging the distances derived from the 5 fittest foragers. These 10 mean
distances were collected for each of the three input conditions. Because we
have 10 replications, the 10 means for each distance can be used as dependent
variables in two separate analyses of variance, one for within-category, the
other for between-category distances. Our MANOVA for the within-category
distances had two independent variables: LEARNING CONDITIONS with 3 levels
(Pre, No, Toil) and CATEGORY TYPE with 4 levels (Eat, Mark, Return, Do-nothing)
(note 2).
We used a
repeated measure MANOVA because all levels of CATEGORY TYPE and LEARNING
CONDITIONS involve repeated measures in the same set of nets. (We excluded the
Theft condition in which the within-category distance is 0 because all ten
samples of mushrooms use the same call input.) The chart of the average
within-category distances in the 4x3 conditions is shown in Figure 8.
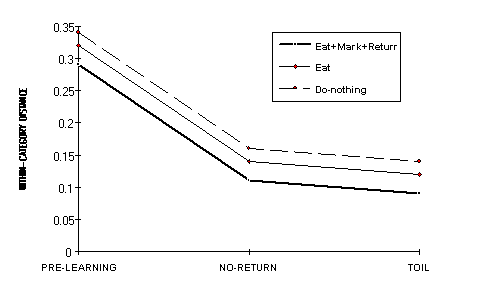
Figure 8 - Average within-category distances in the three conditions. The curve for Mark is not shown because it coincides with the curve for Eat.
The two
main effects are statistically significant ( F(2,18)=917.6 and p<0.00001 for
LEARNING and F(3,27)=18.8 and p<0.00001 for CATEGORY TYPE); the interaction
is not significant. Using the post-hoc Duncan test with a significance
threshold of p<.01 to compare the means for each independent variable, all
the comparisons in the LEARNING condition were significant. That is,
within-category distances decrease significantly from Pre-learning to No-return
to Toil. The biggest decrease is between the (random) Pre-learning and all the
post-learning nets (Figure 8). In the four levels of CATEGORY TYPE, all means
differ from each other except the Eat and Mark within-distances. That is, the
within-category distance for Eat and Mark is the same, whereas the within
distance of Do-nothing is the biggest and that of Return the smallest.
MANOVA for
the between-category distances had two repeated variables: LEARNING CONDITIONS
with 4 levels (Pre, No, Toil, Theft) and CATEGORY COMPARISONS with 4 levels
(Eat Versus Mark, Eat vs Return, Eat vs Do-nothing, Return vs Do-nothing). The
Mark vs Return and Mark vs Do-nothing comparisons are not included in the
analysis because their means are very similar to the parallel comparisons Eat
vs Return and Eat vs Do-nothing, respectively (Table 2). We then go on to
generalize the results for the Eat vs Mark comparisons. The between-category
distances for the 4x4 repeated measure design are shown in Table 2 and Figure
9.
Table 2 - Table of means for the MANOVA of within-category distances
|
COMPARISON |
PRE |
NO-RET |
TOIL |
THEFT |
|
EAT « MARK |
.57 |
1.47 |
1.47 |
1.42 |
|
RETURN « EAT |
.42 |
1.01 |
1.10 |
1.25 |
|
RETURN « MARK |
.39 |
1.01 |
1.12 |
1.25 |
|
EAT « Do-nothing |
.42 |
1.04 |
1.02 |
.93 |
|
MARK « Do-nothing |
.45 |
1.04 |
1.02 |
.95 |
|
RETURN « Do-nothing |
.54 |
1.42 |
1.52 |
1.61 |
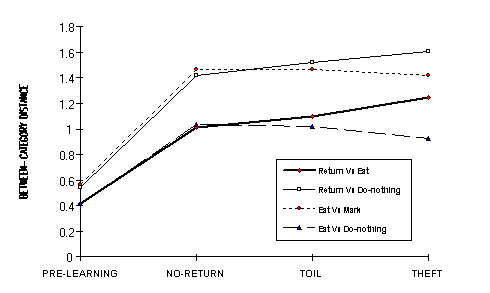
Figure 9 - Between-category distances in the four conditions. Return vs Mark and Mark vs Do-nothing are not shown because they are congruent with Return vs Eat and Eat vs Do-nothing respectively.
The two
main effects are significant ( F(3,27)=3771.6 and p<0.00001 for LEARNING and
F(3,27)=868.6 and p<0.00001 for COMPARISONS) as is their interaction
(F(9,81)=75.7 and p<.00001). Duncan tests revealed, first, a significant
difference in the distance between the Pre-learning nets and all the
post-learning nets. (This expected effect only shows that any kind of
systematic learning will increase between-category distances compared to random
initial distances.) Comparing Toil vs Theft specifically, we see that all
distances between Return and the other three categories are greater in the
Theft nets. Learning Return by Theft has the effect of separating this category
more from the others. The mean differences were all significant for Return vs
Eat, Return vs Mark, and Return vs Do-nothing, 1.25, 1.25 and 1.25,
respectively, in the Theft nets, and 1.10, 1.12, and 1.52 in the Toil nets. The
Theft learning of Return caused the between-category distances not involving
Return to decrease. [A last effect is that in all learning conditions the Eat
vs Mark and Return vs Do-nothing distances are greater then the other pairs
because the Hamming distances of their I/O codes are maximal (e.g. features A
and B for Eat Vs Mark have the input contrast: 10 Vs 01).]
Figure 10
shows the change in the distances between the internal representations of the A
(Eat only), B (Mark only), A&B (Eat & Mark & Return), and
not-A¬-B (neither Mark nor Eat nor Return) Mushrooms. Prior to Toil, the
circles, proportional to the within-category distances, are large, and the
rectangle, proportional to the between-category distances is small. After Toil
learning, the within-category differences shrink and the between-category
distances expand.
Figure 11
then traces the between-category expansion to Theft Learning: The thin dashed
rectangle is proportional to the between-category distances before learning
(random). The thick dashed line is what they look like after Toil learning of
Eat and Mark without Return; the thin continuous line is identical to Figure 9,
that is, Toil learning of Eat and Mark, with Return, and the thick continuous
line is for Theft learning of Return. Note the increased separation between
A&B and not-A¬-B induced by Theft alone.
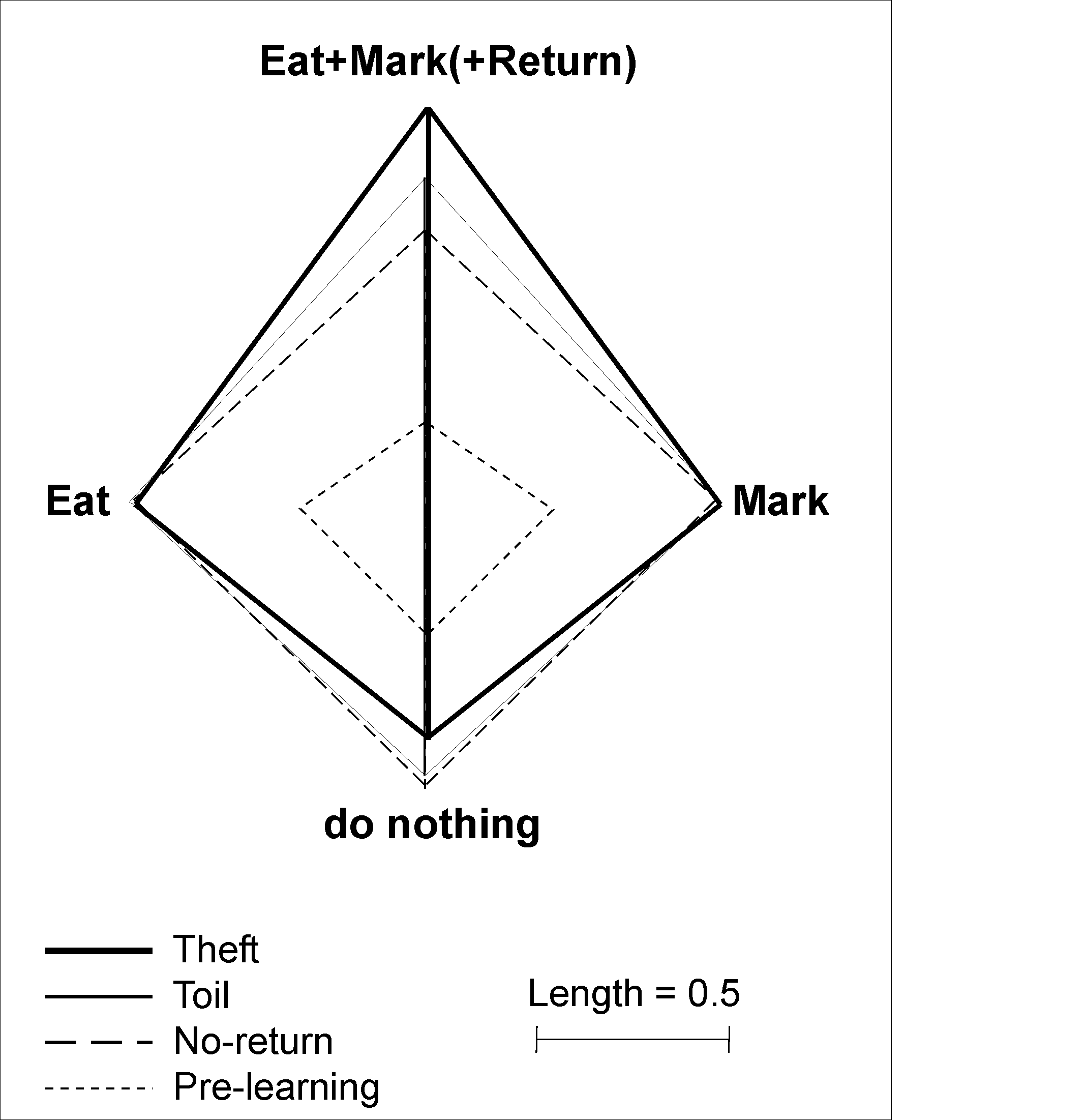
Figure 10 - 2D projections of between-category distances (quadrilateral sides) and within-category distances (circle radius) in the Pre-learning condition and after Toil learning of Eat, Mark,and Return. All distances except Eat vs Mark correspond to the actual Euclidean distances in 5 dimensional hidden unit space.
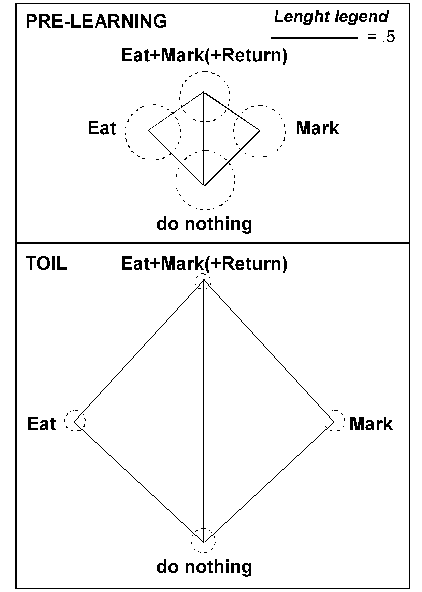
Figure 11 - 2D projections of the between-category distances (quadrilateral sides) in the four conditions. All distances, except Eat vs Mark, are comparable and reflect the actual Euclidean distances between categories (cf. length legend). Note that the distances between Return and all the other categories (Return vs Eat, Return vs Mark, Return vs Do-nothing) are the highest in the Theft condition.
8. Conclusions
We have
shown that a strategy of acquiring new categories by Symbolic Theft completely
outperforms a strategy of acquiring them by Sensorimotor Toil as long as it is
grounded in categories acquired by Toil. The internal mechanism that makes both
kinds of category acquisition possible does so by deforming or “warping”
internal similarity space so as to compress the internal representation of members
of the same category and to separate those of different categories. The warping
occurs primarily in the service of Toil, but Theft not only inherits the warped
similarity space but can warp it further. This warping of similarity space in
the service of sensorimotor and symbolic learning is called categorical
perception and can be interpreted as a form of Whorfian effect (Whorf, 1964) in
which language influences how the world looks to us.
From the
standpoint of our Martian anthropologist, the influence would run roughly like
this: All other species on this planet
get their categories by toil alone, either cumulative, evolutionary toil or
individual lifetime toil: Individuals encounter things, must learn by trial and
error what to do with what, and to do so, they must form internal
representations that reliably sort things into their proper categories. In the
process of doing so, they keep learning to see the world differently, detecting
the invariants, compressing the similarities and enhancing the differences that
allow them to sort things the way they need to be sorted, guided by feedback
from the consequences of sorting adaptively and maladaptively (as in the
mushroom world).
That’s how
it proceeded on our planet until one species discovered a better way: First
acquire an entry-level set of categories the honest way, like everyone else,
but then assign them arbitrary names. (Those names could start as nonarbitrary
functional or imitative gestures at first, by-products of practical, collective
social actions or even deliberate mimicry, but their nonarbitrary features
would be irrelevant once they were used just to name; and vocal gestures would
be least encumbered with other practical tasks, hence most readily available
for arbitrary naming, especially across distances, out of eye-shot, and in the
dark.) Once the entry-level categories had accompanying names, the whole world
of combinatory possibilities opened up and a lively trade in new categories
could begin (probably more in the spirit of barter than theft, and, within a
kin-line, one of sharing categories along with other goods). In trading
categories as they traded combinations of symbols, our species also traded
“world-views,” for each category acquired by hearsay also brought with it some
rearrangement of the internal representation of categories, a “warping” that
was Whorfian, whether merely the subtle compression that results from learning
that A is always conjoined with B, or the fundamental restructuring dictated by
a radical scientific discovery.
Only our
Martian knows the specific initial conditions in which the generative power of
names and their boolean combinations made themselves felt biologically on our
planet, but perhaps our simulations suggest how its benefits might have
mushroomed, inducing a series of Baldwinian adaptations inclining ever our
successful ancestors to name categories and to string names together so as to
describe new categories to one another with ever more fervor and commitment.
Can results
from a 3-bit toy world really cast light on the rich and complex phenomenon of
the origin and adaptive value of natural language? This is really a question
about whether such findings will “scale up” to human size in the real world.
This scaling problem -- common to most fields of cognitive modeling where the
tasks themselves tend not to be lifesize or to have face validity -- can only
be solved by actually trying to scale our models upward, incorporating more and
more of the real-world complexity and constraints into them. This is how our
own research program will continue. In this paper, however, we wanted to enter
our own toy candidate into the competition with the other toy models
(tool-make, hunt-help, chit-chat, etc.; Knight et al., 2000) for the provenance
of our species’ most powerful and remarkable trait. In other work, we have investigated categorical perception with
continuous stimuli (Tijsseling & Harnad, 1997), the transfer of grounding
to higher-order categories (Cangelosi, Greco & Harnad, 2001) and the
emergence of syntax and compositional languages (e.g. Cangelosi, 2001).
References
Andrews, J., K. Livingston, and S.
Harnad. 1998. Categorical perception effects induced by category learning. Journal of Experimental Psychology: Human
Learning and Cognition. 24(3): 732-53
Cangelosi, A. 2001. Evolution of
communication and language using signals, symbols and words. IEEE Transactions in Evolutionary
Computation, 5(2): 93-101
Cangelosi, A., A. Greco, and S. Harnad.
2000. From robotic toil to symbolic theft: Grounding transfer from entry-level
to higher-level categories. Connection
Science, 12: 143-162
Cangelosi, A.,
and D. Parisi. 1998. The emergence of a "language" in an evolving
population of neural networks. Connection
Science, 10: 83-97
Cangelosi, A. and D. Parisi. 2002. Simulating the evolution of language.
London: Springer-Verlag
Catania, A.C. and S. Harnad. (Eds.).
1988. The selection of behavior. The
operant behaviorism of BF Skinner: Comments and consequences. New York:
Cambridge University Press.
Csato, L., G. Kovacs, S. Harnad, R.
Pevtzow, and A. Lorincz. Submitted. Category learning, categorization
difficulty, and categorical perception: Computational and behavioral evidence. Connection Science.
Gibson, J.J. 1979. An ecological approach to visual perception.
Boston: Houghton Mifflin
Goldberg, D.E. 1989. Genetic algorithms in search, optimization,
and machine learning. Reading, MA: Addison-Wesley.
Goldstone, R. 1994. Influences of
categorization on perceptual discrimination.
Journal of Experimental Psychology: General, 123:178-200
Goldstone, R.L., M. Steyvers, M.,
and K. Larimer. 1996. Categorical perception of novel dimensions. In Proceedings of the Eighteenth Annual
Conference of the Cognitive Science Society.
Harnad, S. 1976. Induction,
evolution and accountability. Annals of
the New York Academy of Sciences 280: 58-60.
Harnad, S. (Ed.) 1987. Categorical Perception: The groundwork of
cognition. New York: Cambridge University Press.
Harnad, S. 1990. The Symbol
Grounding Problem. Physica D 42:
335-346.
Harnad, S. 1992. Connecting Object
to Symbol in Modeling Cognition. In A. Clark and R. Lutz (Eds.) Connectionism in context Springer
Verlag, pp 75 - 90.
Harnad, S. 1993. Grounding symbols
in the analog world with neural nets. Think
2(1): 12-78 (Special issue on
"Connectionism versus Symbolism," D.M.W. Powers & P.A. Flach,
eds.).
Harnad, S. 1995. Grounding symbolic
capacity in robotic capacity. In L. Steels, and R. Brooks (Eds.) The Artificial Life route to Artificial
Intelligence: Building embodied situated Agents. New Haven: Lawrence
Erlbaum. pp. 277-286.
Harnad, S. 1996a. The origin of
words: A psychophysical hypothesis In B. Velichkovsky B and D. Rumbaugh (Eds.) Communicating Meaning: Evolution and Development
of Language. NJ: Erlbaum: pp 27-44.
Harnad, S. 1996b. Experimental
analysis of naming behavior cannot explain naming capacity. Journal of the Experimental Analysis of
Behavior 65: 262-264.
Harnad, S., S.J. Hanson and J.
Lubin. 1991. Categorical Perception and the evolution of supervised learning in
neural nets. In DW Powers & L Reeker (Eds.), Working Papers of the AAAI Spring Symposium on Machine Learning of
Natural Language and Ontology. pp. 65-74.
Harnad, S., S.J. Hanson and J.
Lubin. 1995. Learned categorical perception in neural nets: Implications for
symbol grounding. In V. Honavar & L. Uhr (Eds.) Symbol processors and connectionist Network models in artificial
intelligence and cognitive modelling steps toward principled integration.
Academic Press. pp. 191-206.
Harnad, S., H.D. Steklis and J.B
Lancaster. (Eds.) 1976. Origins and evolution of language and speech. Annals of the New York Academy of Sciences,
280.
Kirby, S. 2000. Syntax without
natural selection: How compositionality emerges from vocabulary in a population
of learners. In C. Knight, M. Studdert-Kennedy, J.R. Hurford (eds), The evolutionary emergence of language:
Social function and the origins of linguistic form, Cambridge University
Press, pp 303-323
Knight, C., M.
Studdert-Kennedy, and J.R. Hurfor. 2000. The
evolutionary emergence of language: Social function and the origins of
linguistic form, Cambridge University Press
Livingston, K.R. and J.K. Andrews.
1995. On the interaction of prior knowledge and stimulus structure in category
learning. Quarterly Journal of
Experimental Psychology Section A-Human Experimental Psychology, 48:
208-236.
Nakisa, R.C., and K. Plunkett. 1998
Evolution of a rapidly learned representation for speech. Language and Cognitive Processes, 13: 105-127
Parisi, D., F. Cecconi, and S.
Nolfi. 1990. Econets: neural networks that learn in an environment. Network, 1:149-168.
Pevtzow, R. and S. Harnad. 1997.
Warping similarity space in category learning by human subjects: The role of
task difficulty. In M. Ramscar, U. Hahn, E. Cambouropolos and H. Pain (Eds.), Proceedings of SimCat 1997:
Interdisciplinary Workshop on Similarity and Categorization. Department of
Artificial Intelligence, Edinburgh University, pp.189-195.
Rumelhart, D.E, G.E. Hinton G.E. and
R.J. Williams. 1986. Learning internal representations by error propagation. In
D.E. Rumelhart and J.L McClelland (Eds.), Parallel
Distributed Processing: Exploration in the microstructure of cognition,
Cambridge, MA: MIT Press, vol. 1
Steels, L. 1997. The synthetic
modeling of language origins, Evolution
of Communication, 1: 1-34.
Steels, L. 2002. Grounding symbols
through evolutionary language games. In A. Cangelosi & D. Parisi, Simulating the evolution of language.
London: Springer-Verlag
Steels, L., and F. Kaplan 1999.
Collective learning and semiotic dynamics. In D. Floreano et al. (Eds.), Proceedings of ECAL99 European Conference on
Artificial Life, Berlin: Springer-Verlag, pp. 679-688
Steklis, H.D. and
S. Harnad. 1976. From hand to mouth: Some critical stages in the evolution of
language. In: S. Harnad et al. 1976, pp. 445-455.
Tijsseling, A. and S. Harnad. 1997.
Warping similarity space in category learning by backprop nets. In M. Ramscar,
U. Hahn, E. Cambouropolos and H. Pain (Eds.), Proceedings of SimCat 1997: Interdisciplinary Workshop on Similarity
and Categorization. Department of Artificial Intelligence, Edinburgh
University, pp.263-269.
Whorf, B.L. 1964. Language, thought and reality. Cambridge
MA: MIT Press
Notes
(1) In simulations conducted by Emma
Smith and Gianni Valenti (unpublished data, BSc Theses, Department of
Psychology, University of Southampton, 1997) we have shown that when the
scarcity of the mushrooms is varied, Theft beats Toil when there are plenty of
mushrooms for everyone, but when the mushrooms are scarce and vocalizing risks
losing the mushroom to the Thief, Toil beats Theft and the foragers are mute.
Further studies analyzing kinship showed that under conditions of scarcity
vocalizing to relatives only beats vocalizing to everyone. Of course a mushroom
world is too simple, and foraging categories are not the only ones that can
benefit from Theft. The pattern may be different for categories related to
danger, territory, mating, dominance, or instructing offspring.
(2) We will use the names Eat, Mark,
Return, and Do-nothing (i.e. non-A, non-B mushrooms) to refer to the four
categories. Return categories could also be called Eat+Mark+Return because the
Return category implies the co-occurrence of behaviors/calls Eat and Mark