Dimensional Distinctiveness or Interference With Recall At Five Seconds After Stimulus Presentation?
Comment on “The Shift From Recency To Primacy With Increasing Delay” by Knoedler, Hellwig and Neath (Journal of Experimental Psychology: Learning, Memory and Cognition, 1999, Vol 25, No. 2, 474-487)”
by
Eugen Tarnow, Ph.D.
Avalon Business Systems, Inc.
3725 Blackstone Avenue, Ste. 4E
Riverdale, NY 10463
(718) 884-1819 (voice)
(208) 445-3638 (fax)
etarnow@avabiz.com (e-mail)
Abstract:
Knoedler, Hellwig and Neath presented measurements of the recency-primacy shift in which memory for early list items improves and memory for later items becomes worse as the retention interval between study and test increases. The authors interpreted the data to support the Dimensional Distinctiveness model. I present an alternative interpretation of their data in terms of an interference model, “Early Interference with Recall”, at five seconds after the presentation of a particular list item and show that this interpretation can qualitatively better account for the experimental data. Two predictions further separate the two models: Dimensional Distinctiveness predicts no recency-primacy shift for two-item lists, in contrast to Early Interference With Recall. As the overall time scale is changed, the former model also predicts no difference in recency or primacy while the latter shows large changes.
��Introduction
Neath (p. 151, 1998) wrote that “any theory of forgetting must explain not only why memory is often worse as time passes, but also why memory is sometimes better.” He and other authors have focused their attention on an interesting anomaly in experimental memory research, the recency-primacy shift. This shift was the subject of a previous paper in this journal, Knoedler, Hellwig and Neath (1999). The authors there presented data which showed the recency-primacy shift under a variety of conditions. They explained the experimental data using the Dimensional Distinctiveness model. The present comment suggests that the Dimensional Distinctiveness model, as elaborated in their paper, does not fit the data and that a better explanation is one in which the information storage process interferes with the recall process about five seconds after the presentation of a simulus.
Graphing the data as a function of time
I graph the data somewhat differently than was done in the original article. In Figure 1 is shown the proportion of correctly tested list items as a function of the delay in seconds between the test and the study of each item for four item series and four retention intervals. The recency-primacy shift is the secondary difference in proportion correct answers between the first and 4th position at 0 and at 5 second retention intervals - at 0 seconds this difference is negative, at 5 seconds it is positive (in each series the 4th and latest position shows up first in my graphs). As remarked in the paper and in Neath (1998), any theory of memory has to account for this shift, in particular, for the rather amazing result that the memory of the 4th position actually improves with increased study-test time! The recency-primacy shift is relatively small - the secondary difference is only about 0.1.
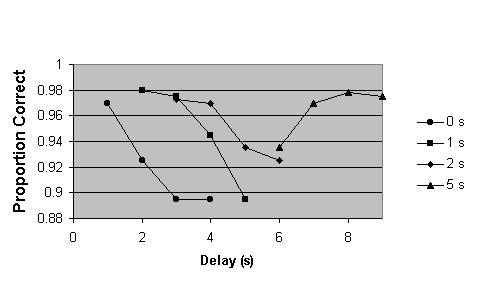
Figure 1. Mean accuracy (proportion correct as measured by hits) for four-item study/test series as a function of the delay between study and test for four retention intervals (0,1,2 and 5 seconds).
Simulation of the data using the Dimensional Distinctiveness model
The Dimensional Distinctiveness model would simulate the data as shown in Figure 2 (I normalized the data for the first test item at 0 seconds to 0.97; the baseline in the experimental data of Figure 1 is dependent on the relatively small subject sample and the simulations that follow reflect that particular subject group). There are several important observations to make. First, the two intermediate list items show exactly the same relative distinctiveness, no matter the retention interval and their absolute distinctiveness is just around 0.55 and varies little. This is in contradiction to the experimental data in Fig. 1 in which the two intermediate items varies just as much as the first and last list items and seems to exchange values as the retention interval increases. Second, while the model predicts the correct direction of change of the first and last list items, the two items never reverse as they do in the experimental data and there is no recency-primacy shift. Indeed, as the retention interval increases the distinctiveness of the first item becomes equal to the distinctiveness of the last item, 0.83 and exactly 1.5 as large as the distinctiveness of the intermediate list items. Third, the overall scale of changes in proportion correct as a function of delay is five times larger than found in experiment.
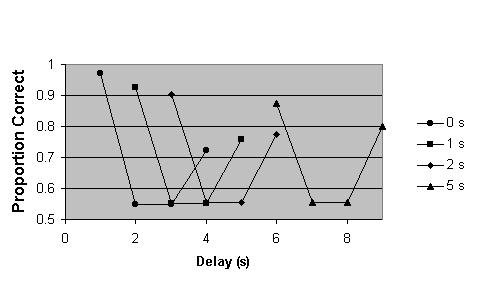
Figure 2. Simulation of the mean accuracy for four-item study/test series as a function of the delay between study and test for four retention intervals (0,1,2 and 5 seconds) using the Dimensional Distinctiveness model.
An unusual feature of the Dimensional Distinctiveness model is not shown in the picture: while the distinctiveness score is time dependent, it does not scale with time. I.e. if the experiment took place over 9 seconds or 18 seconds (or, indeed 18 years), the model would predict the same result as long as the list items had the same relative time relationship.
Simulation of the data using Early Interference with Recall model
Let us be guided by Neath’s remark that memory is improving with time in the recency-primacy shift (Neath, 1998). It is not inconceivable that the storage process during the study time could interfere with the recall process at some later time and this is the basis for my Early Interference with Recall alternative model of the recency-primacy shift. Let us attempt to simulate the result of Fig. 1 using a self-interference term (item storage process interfering with recall of the same item) at about five seconds after the stimulus presentation.
I simulate this interference process using an exponential function
Interference = -a*exp(-(ts-tt-N)2/2s2)
centered at N seconds with a width s where ts is the time of study and tt is the time of the test. Using the parameters N=4.8 and a=0.074 and s=2.4 I obtain the graph of Figure 3. Two features are qualitatively similar to the experimental data in Figure 1. First there is a dip in the data around five seconds after the study. This dip automatically leads to the “recency-primacy” shift. Second, the intermediate list items are reproduced correctly - they vary just as much as the first and last list items, are not always the same and change relationships after the five second dip.
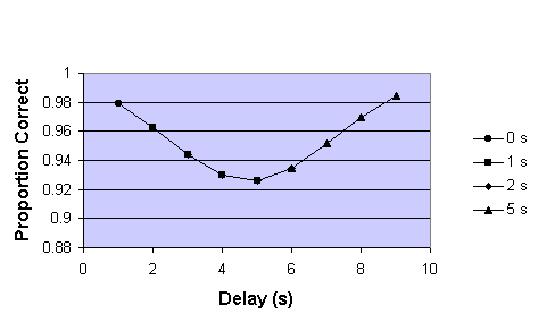
Figure 3. Simulation of the mean accuracy for four-item study/test series as a function of the delay between study and test for four retention intervals (0,1,2 and 5 seconds) using the Early Interference with Recall model.
If we add a small amount of inter-item interference the model fits the data even better and makes the test results dependent not only on the delay time between study and test, but also on the position of the item in the list. The result for 0.63% more erroneous recall for each previous presentation and N=4.6 and a=0.068 and s=2.1 in the series is shown in Figure 4. The secondary interference causes the curves to split.
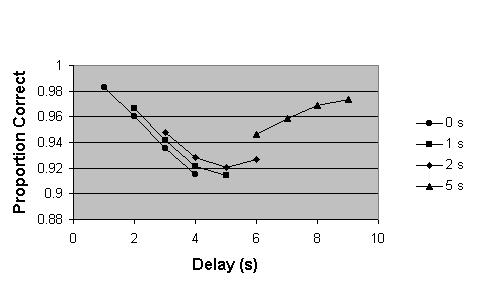
Figure 4. Simulation of the mean accuracy for four-item study/test series as a function of the delay between study and test for four retention intervals (0,1,2 and 5 seconds) using the Early Interference with Recall model including a 0.63% inter-item interference term.
Comparison between the two models and predictions to further separate them
The Early Interference with Recall model is superior to the Dimensional Distinctiveness model in several ways: It gives the correct qualitative results for the recency-primacy shift, not just the correct direction of change, it gives the correct qualitative results for the intermediate items rather than making the two the same. It may give a more intuitive explanation for why memory seems to be getting better with time (recall is getting better, storage is not), one which does not involve organizing memory perceptually.
There are several other ways these two models predict different experimental results. Most importantly, the Dimensional Distinctiveness model predicts that there is no recency-primacy shift for two-item series, in contradiction to the prediction of the Early Interference with Recall model in Figure 5. Secondly, the Early Interference with Recall model depends strongly on the time scale, while the Dimensional Distinctiveness model has no dependence on the time scale - multiplying the experimental time scales by five will yield the same prediction for the Dimensional Distinctiveness model but the prediction of Fig. 6 from the Early Interference with Recall model.
Finally, the Early Interference with Recall model shows an interesting balance of inter-item and intra-item interference effects. If one increases the ratio of intra-item to inter-item interference, the model predicts that the recency primacy shift should disappear.
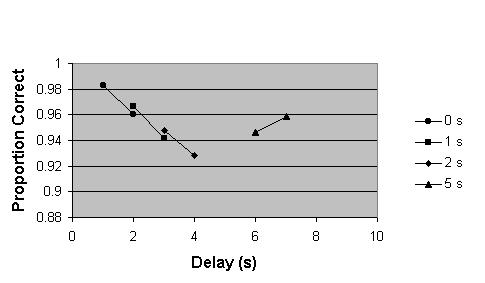
Figure 5. Prediction of the mean accuracy for two-item study/test series as a function of the delay between study and test for four retention intervals (0,1,2 and 5 seconds) using the Early Interference with Recall model including a 0.63% inter-item interference term. Notice the predicted recency-primacy shift.
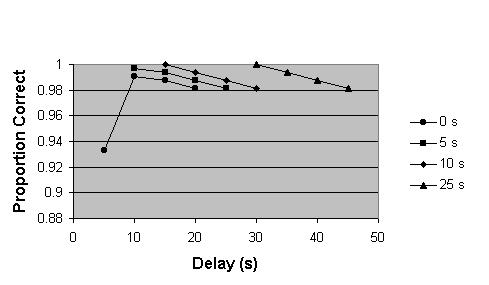
Figure. 6 Prediction of the mean accuracy for four-item study/test series as a function of the delay between study and test for four retention intervals using the Early Interference with Recall model including a 0.63% inter-item interference term. All time scales are five times larger than in previous figures.
�REFERENCES
Knoedler, A.J., Hellwig and Neath, I. (1999), “The Shift From Recency To Primacy With Increasing Delay “, Journal of Experimental Psychology: Learning, Memory and Cognition, 1999, Vol 25, No. 2, 474-487.
Neath, I (1998). “Human Memory”. Brooks/Cole. Pacific Grove. 148-151.





