Journal of Experimental Psychology:
Human Learning and Memory
1979, Vol. 5, No. 2, 160-169
(c) Copyright 1979 American Psychological Association, Inc.
Response Latencies in Discriminations of Recency
Paul Muter
University of Toronto, Toronto, Canada
Abstract: Subjects were asked to report which of two test words had been presented more recently in a list of 4 or 10 words. In each of four experiments, the study position of the probe that had been presented earlier in the list had little or no effect on response latency, whereas the study position of the probe that had been presented later in the list had a large and reliable effect on response latency. In Experiment 4, some test items were lures, and they had no effect on response latency. These results are incompatible with several theories of recency discrimination and strongly suggest parallel self-terminating processing of the probes.
If a person experiences several events and is later asked which of two of the events occurred more recently, he can answer correctly above the chance level. How is this task performed? There are several theories of recency discrimination in the psychological literature, but evidence relating to these theories is inconclusive. The present article presents new data relevant to the task of recency discrimination and suggests a new theoretical interpretation that is consistent with these and other data.
The question of how recency discriminations are made is of intrinsic interest, but in addition, recency discriminations may play a critical role in many memory and learning tasks. In forced-choice recognition, for example, the subject's response may be an indication of which item has been encountered more recently. And Postman (1963) has suggested that in many transfer situations, judgments of recency may underlie performance.
There are two basic questions relevant to the task of recency discrimination. First, how is recency information for a single event coded and retrieved? Second, how are recencies of two events discriminated? With respect to the first question, four proposals will be briefly described: strength theory, the conveyor-belt model, attribute theory, and the notion of time tags.
Strength theories of judgments of recency extend back at least to Lipps (1883/1963), but more modern versions have been articulated by Hinrichs (1970), Konorski (1961), Morton (1968), and Peterson (1967). According to strength theories, the strength of a memory trace of an event is at a peak shortly after the event and declines thereafter. At the time of test, the memory trace of the event is somehow accessed directly, and the strength of the trace is assessed. The judgment of recency is then derived from the strength, where recency is assumed by the system to be a monotonic function of strength. (Using similar reasoning, Wickelgren, 1974, assumed that the judgment of recency is based on the fragility of the trace, where fragility decreases over time.)
The conveyor-belt model was foreshadowed by Guyau (1902/1963), but amore detailed version has been proposed by Murdock (1972, 1974; Murdock & Anderson, 1975). Representations of events are assumed to be added to memory as suitcases to a conveyor belt, and when a test item is perceived, a backward scan along the conveyor belt is initiated. When a memory trace is encountered which matches the test item to a certain criterion, the search is terminated. A counter, which is incremented each time a new trace is examined, indicates the recency of the test item.
According to attribute theory (Bower, 1972), at the time of study, a subset of an item's attributes is "marked" and becomes part of the "active set." During the retention interval, there is some fluctuation of attributes between the active and inactive sets, and the number of marked attributes in the active set tends to decrease as time passes. Bower proposed that judgments of recency are based on the number of marked attributes in the active set at the time of test.
Finally, Yntema and Trask (1963) suggested the notion of a time tag. The assumption here is that one component of the memory trace of a past event is a tag that in some way directly indicates when the event occurred. As "time tag" is defined in the present article, strength and marked attributes are not time tags because they can provide temporal information only indirectly. Berlyne (1966) did not use the phrase "time tag," but he argued that a counter is incremented whenever any study item is presented and that the value of this counter at the time of study of a particular item becomes associated with that item.
It is clear that there is no consensus on the issue of how recency information for an event is coded and retrieved. With respect to the issue of how relative recency is determined, it is generally assumed, at least implicitly, that the recencies of the two test items are determined, either successively or in parallel, and that these two recencies are then compared. However, it is possible that the two test items are processed in parallel and that processing stops as soon as relevant processing for one item has been completed, or as soon as a criterion on some dimension has been reached for one of the items. This item would then be reported to be more recent, and the recency of the other probe would not be determined. In short, it is possible that processing of the two test items is parallel and self-terminating, rather than exhaustive. (The phrase "parallel self-terminating processing of the probes" denotes parallel self-terminating processing of the test list, not parallel self-terminating processing of the set of traces in memory.) This parallel self-terminating possibility was suggested by Murdock and Anderson (1975) in the context of recognition memory. They argued that in forced-choice recognition, a search proceeds backward along the conveyor belt and terminates when a trace that matches any of the probes is found. To my knowledge, the strength and attribute theorists have not discussed in print the possibility of parallel self-terminating processing of the probes, but the parallel self-terminatitig view could be coupled with the strength view or the attribute view: The strengths of the two probes could be assessed in parallel, or marked attributes could be counted in parallel. The parallel self-terminating view is probably incompatible with the time-tag view. Presumably it is not possible to read in parallel two digital tags and stop when one reaches a criterion.
To my knowledge, no studies of discriminations of recency using response latency as a dependent measure have been published. The experiments described here were undertaken with the expectation that response latencies would shed light on processing in discriminations of recency. So, in part, Experiment I was exploratory. However, some of the proposals described make different predictions about the effects of the study positions of the two probes on the latency of correct responses.
If the conveyor-belt model is correct and if the probes are processed exhaustively and successively, then latency should be slower for earlier study positions of each probe (Figure 1a), since a scan will be executed back to one item, then a second scan will be executed back to the other item, and scanning is assumed to take at least a few milliseconds/item (Murdock, 1974; Sternberg, 1969). (The conveyor-belt model always assumes self-terminating processing of the conveyor belt regardless of whether the processing of the probes, that is, the test list, is self -terminating or exhaustive.) If the probes are processed exhaustively in parallel, then the conveyor-belt model predicts that latency should be slower for earlier study positions of the earlier probe but unaffected by the study position of the later probe (Figure lb), since the time required to find a match for the earlier probe would be longer than the time required to find a match for the later probe. If the conveyor-belt model is correct but the processing of the probes is parallel and self-terminating (Murdock & Anderson, 1975), then latency should increase with earlier study positions of the later probe but should not be affected by the study position of the earlier probe (Figure 1c) : The two parallel backward scans would terminate when the trace of the more recent item was found.
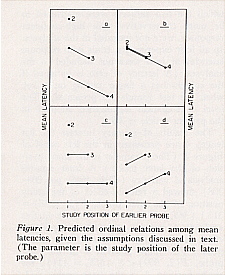
Similarly, if processing of the probes is parallel and self-terminating but strength theory or attribute theory is correct, then latency should not be a function of the study position of the earlier probe but should be a function of the study position of the later probe (Figure 1c), assuming that the rate of accumulating assessed strength or counting marked attributes is a function of the amount of strength or the number of marked attributes, respectively. As a final example, if strength theory is correct but the probes are processed exhaustively, then for a given study position of the later probe, latency may be faster for earlier study positions of the earlier probe (Figure 1d) if the effect on latency of ease of comparison of strengths is sufficiently great.
Experiment 1
It is possible that processing in discriminations of recency is fundamentally different below memory span than above memory span. In Experiment 1, list length was sometimes 4 and sometimes 10. Subjects saw a list of words, presented one at a time, followed by two simultaneous test words, both from the list.
Method
Subjects. In all four experiments, subjects were right-handed undergraduates at the University of Toronto who had responded to a notice requesting subjects for a memory experiment. They were paid for their participation. There were four subjects in each experiment
Apparatus and stimuli. Randomization and presentation of stimuli were controlled by a PDP12A computer. Subjects sat in front of a cathode-ray screen, and on each trial they responded by pressing one of six keys resting under their fingers. The distance between the screen and the subjects' eyes was approximately 75 cm. The height of the uppercase letters forming the stimulus words was approximately 8 mm, or 6 degrees of visual angle. Trial and response information were recorded automatically on magnetic tape. The stimulus words were drawn from a pool of 512 common two-syllable English nouns not more than eight letters long, with homophones, contractions, archaic words, and proper nouns excluded.
Procedure. A trial consisted of the following sequence. The message WHEN READY PRESS ANY KEY appeared on the screen. Starting 500 msec after the subject pressed any key to indicate that he was ready, the list of 4 or 10 words was presented at the rate of 500 msec/word (a word for 475 msec followed by a blank screen for 25 msec). After a 1-sec pause, two randomly selected different test words, both from the list just presented,were displayed and remained on the screen until the subject pressed a key. A message, either RIGHT or WRONG, appeared for 500 msec. Then the message WHEN READY PRESS ANY KEY appeared again, and so on.
The two test words were displayed one above the other, with the top word appearing in the same vertical position as the words in the study list. The distance between the bottom of the top test word and the top of the bottom test word wasapproximately 10 cm, or 7 degrees and 30 minutes of visual angle. All words, study and test, were centered on the screen with respect to the left-right dimension.
A block consisted of 45 trials. Within each block, words were randomly sampled, without replacement, from the pool of 512 words; that is, each list consisted of words that had not been presented before in that block. Subjects were not informed of this constraint. They were simply instructed to press Key 1, 2, or 3 if the top test item had been presented more recently in the list, and Key 4, 5, or 6 if the bottom test item had been presented more recently in the list. They were asked to press Key 1 or 6 if they were quite sure of their response, 3 or 4 if they were virtually guessing, and 2 or 5 otherwise. (This confidencejudgment procedure yields a pool of responses that is less contaminated by correct guesses than is the pool of all correct responses.) Keys 1, 2, and 3rested under the left hand; Keys 4, 5, and 6 were under the right hand. Subjects were repeatedly told that speed and accuracy were both important, and equally important. At the end of each session, subjects were informed how many correct and incorrect responses they had made with each key. At the end of each block of trials, a number indicating mean response latency for that block appeared on the screen.
In each session there were seven blocks of trials. For one of the seven blocks, selected at random, the list length was 4; for the other six blocks, the list length was 10. (There were more blocks at list length 10 than list length 4 because the number of possible combinations of early and late study positions is much greater for the longer list length.) Before each block, a message indicating the list length for the upcoming block was displayed on the screen for 3 sec. Rest periods were permitted at any time. The four subjects completed thirteen 45-min sessions each, at the rate of approximately four sessions/week. Subjects were informed that the first session was for practice only, and data from practice sessions were not included in any analyses.
Results and Discussion
A total of four early sessions from two subjects, in which the accuracy on high-confident responses was very low and after which the two subjects were instructed to be more conservative with high-confident responses, were not included in the analyses. In all four experiments, trials with response latencies of zero were not included in the analyses. (A latency of zero is obtained if the subject has a finger resting on a key when the test stimuli are presented.) The level of statistical significance adopted in the present article is .05.
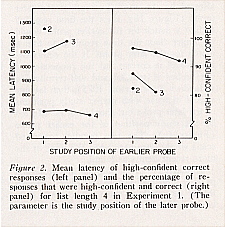
The results of primary interest for list length 4 are presented in the left panel of Figure 2. (The parameter is the study position of the later probe.) A least squares analysis of variance (Kirk, 1968, pp. 204-208) showed a reliable effect of the study position of the later probe, F(2, 1748) = 313.1 (MSe = .177). Two least squares analyses of variance revealed no significant effect of the study position of the earlier probe: For study position 4 of the later probe, F (2, 899) < 1 (MSe = .111); for study position 3 of the later probe, F(l, 544) = 2.46 (MSe = .266). The right panel of Figure 2 indicates, for each combination of study positions, the percentage of responses that were both high-confident and correct, and therefore that are represented in the left panel.
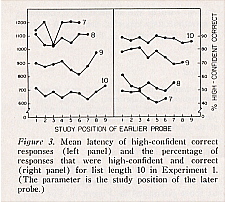
The left panel of Figure 3 contains the results of primary interest for list length 10. (Data for study positions of the earlier probe less than seven are not included in Figure 3 because standard errors of estimate are very high, primarily because of the low number of high-confident correct observations at each point.) Again, there is a clear effect on latency of the study position of the later probe, F(3, 5394) = 448.9 (MSe = .141). With respect to the effect on latency of the study position of the earlier probe, the results are not as clear as for list length 4. Analyses of variance show a significant effect for study position 10 of the later probe, F (8, 2050) = 2.03 (MSe = .104), and for study position 7 of the later probe, F(5, 673) = 3.34 (MSe = .200). Unfortunately, the two nonflat functions are nonmonotonic, they do not display a similar pattern to each other, and there is no obvious explanation of the deviations from flatness.
Experiment 2
The results in Experiment 1 may have been affected by the presence of list length as a within-subjects variable. For example, perhaps normally a forward scan would be executed for subspan lists and a backward scan for superspan lists, but the subjects were induced to scan backward on all trials because most of the lists were superspan. (Some data of Sternberg, 1969, Experiment 8, suggested the possibility of a self-terminating forward scan of the memory traces in a subspan order information task.) Experiment 2 was conducted in an attempt to replicate Experiment 1 for list length 4 under conditions in which list length did not vary.
Method
The method for Experiment 2 was identical to that for Experiment 1 with the following exceptions. List length was always 4, there were only 10 blocks of 45 trials in each session, and there were only four sessions/subject, one practice and three experimental. Two of the four subjects pressed a key with their right hand to indicate that the bottom test word was more recent and with their left hand to indicate that the top test word was more recent, and two did the reverse. Keys 3 and 4 were not used: Subjects were asked to press Key 1 or Key 6 if they were quite sure of their response, and Key 2 or Key 5 otherwise. Finally, a slightly more conservative criterion for high-confident responses was induced: Subjects were told that 909% or more of their high-confident responses should be correct.
Results and Discussion
Figure 4 shows that the pattern in Figure 2 was not caused by the presence of list length as a within-subjects variable. As in Experiment 1 for list length 4, latency was affected by the study position of the later probe, F(2, 3050) = 690.8 (MSe = .109), but not by the study position of the earlier probe: F (2, 1809) < 1 (MSe= .084) for study position 4 of the later probe and F(l, 896) < 1 (MSe = .138) for study position 3 of the later probe.
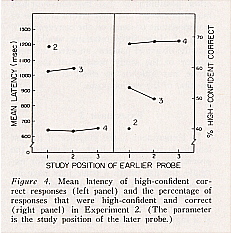
Does latency depend on whether the more recent test word was the top test word or the bottom test word? Experiment 2 provides evidence with respect to this question, since hand (right or left) was counterbalanced. Except for trials on which the study positions of the test items are 1 and 2, the answer is no. On these trials, for some unknown reason latency was reliably faster if the more recent item was in the bottom test position, F(l, 329) = 9.87 (MSe = .160; mean difference = .189 sec). In other words, when the first two items in the study list were tested, latency was reliably faster if the spatial (top-to-bottom) order at test was the same as the temporal order of presentation at study.
Of the four experiments, Experiment 2 was the only one in which there were sufficient incorrect responses in all conditions to provide reasonably stable estimates of mean error latencies. The pattern was very similar to the pattern for high-confident correct responses. One interpretation of this result is that on incorrect trials, processing proceeds normally and correctly before the binary decision and response organization stages (Sternberg, 1969) and that the locus of errors is in one of these later stages. Another possibility is that the conveyor-belt model is correct and that errors are due to transpositions of items on the conveyor belt. Both of these interpretations would predict the observed pattern: an effect on error latency of the study position of the later probe, but little or no effect of the study position of the earlier probe.
Experiment 3
In Experiment 1, the presence of the list length 4 trials may have influenced the processing on list length 10 trials. For example, the list length 4 trials may have induced the subjects to attend largely to the last few items on the list length 10 trials, since subjects knew that they could perform at a high level of accuracy when list length was 4. Two of the subjects in Experiment 1 spontaneously reported using such a strategy. In Experiment 3, list length was always 10.
Method
The method for Experiment 3 was identical to the method for Experiment 2 except that list length was always 10 and the four subjects completed 13 sessions, 1 practice and 12 experimental, of six blocks each.
Results and Discussion
The main results of Experiment 3, portrayed in Figure 5, appear essentially similar to those portrayed in Figure 3. The study position of the later probe had a marked effect on latency, F (3, 4451) = 614.6 (MSe = .066), whereas the study position of the earlier probe had little or no effect, though one of the analyses of variance, for study position 9 of the later probe, showed a reliable effect of the study position of the earlier item, F(7, 1307) = 3.68 (MSe = .077). (For study positions of the later item of less than seven, the number of observations was zero in some cells, and the analyses of variance were not performed.)
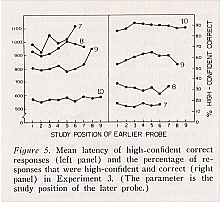
There are insufficient data for study positions 1 and 2 to determine whether experiment 3 replicated the finding from Experiment 2, that on these trials latency was faster when the more recent item was in the bottom test position. However, latencies were faster for the top test position when the study position of the later item was 9, F(l, 1331) = 41.4 (MSe = .076; mean difference = .086 sec), and 10, F(l, 2225) = 62.1 (MSe = .038; mean difference = .068 sec). On an ad hoc basis, this difference can be accommodated by the parallel self-terminating views: The two parallel processes may not start simultaneously - perhaps processing of the top test word begins a few milliseconds before processing of the bottom test word. (The top test word appeared in the same position on the screen as the last study word.) On the other hand, there is no obvious way in which the exhaustive views can accommodate the obtained difference between top and bottom test positions.
Experiment 4
In recency discrimination tasks, if the test items are processed in a parallel self-terminating fashion, then the presence of a lure as a test word should not affect response latency, since as soon as processing of the more recent (or only presented) word is completed, processing of the other test word is terminated. If the test items are processed exhaustively and compared, then the presence of a lure should affect response latency. Experiment 4 was an attempt to demonstrate even more dramatically, by including some nonlist items as probes, that the test item that is not selected as more recent is irrelevant to response latency.
Method
The method for Experiment 4 was identical to the method for Experiment 2, with the following exceptions. On a random 10% of the trials, one of the test words was a word that was not from the just-presented list and had not been presented before in that block of 45 trials. There were no confidence judgments; subjects used only Keys 1 and 6. (Correlational data from the earlier experiments suggested that not only the standard errors of estimate of the mean latencies but also the standard deviations of the latencies were smaller for subjects who used only the high-confidence level most of the time. Because of the extra decision that it requires, the confidence judgment procedure may add more variance than it subtracts.)
Results and Discussion
The results suggest that for a given study position of the later probe, the response latency does not depend on whether the other probe is a lure (see Figure 6). For study positions 2, F(l, 1303) < 1 (MSe = .137), and 3, F(2, 2554) = 1.67 (MSe = .185), of the later probe, the analyses of variance revealed no effect of the study position of the earlier probe, where "lure" was one of the levels of this factor. For study position 4 of the later probe, there was a reliable effect, F(3, 4155) = 3.19 (MSe = .071), but this effect clearly was not caused by the difference between lures and nonlures. Furthermore, this effect is entirely owing to 1 subject, who was the only subject of the 16 subjects in the four experiments who did not reflect the overall pattern with respect to the effect on latency of the study positions of the probes. For this subject the study position of the earlier probe had a marked nonmonotonic effect. If this subject is not included in the analysis, the effect is not significant, F(3, 3135) = 1.38 (MSe = .080).
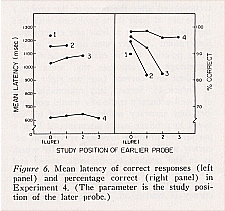
The right panel of Figure 6 indicates that accuracy was enhanced by the presence of a lure. All of the proposals discussed in the introduction can accommodate this result. For the exhaustive theories the explanation is obvious. With respect to the parallel self-terminating views, if the later probe is forgotten, or was not encoded because of a diversion of attention, the subject will guess and be correct 50% of the time if a lure is present, whereas he will be wrong if the other probe is not a lure and not forgotten because he will select it as more recent.
General Discussion
The same pattern emerged in all four experiments: The study position of the earlier probe had little or no effect on latency, whereas the study position of the later probe had a large and reliable effect on latency. The vast majority of analyses of variance showed no effect on latency of the study position of the earlier probe. In Experiment 1, two of the functions were reliably nonflat, and in Experiment 3, one of the functions was reliably nonflat. In these cases in which there was an effect of the study position of the earlier probe, the effects were small, puzzlingly unsystematic, and not those predicted by any of the proposals discussed in the introduction.
The objection could be raised that speed-accuracy tradeoffs may have somehow produced the flat latency functions and that if no such tradeoffs had occurred, the functions would not have been flat. (Before the onset of the probes, subjects cannot determine what the condition is on a particular trial, but perhaps subjects can somehow adjust their criteria as a function of evidence accumulated after the onset of the probes.) There are at least three problems with this argument. First, in at least one experiment, Experiment 2, there was no effect of the study position of the earlier probe on the percentage of responses that were high-confident and correct (see the right panel of Figure 4). Second, any reasonable view of speed-accuracy tradeoffs would not predict that accuracy would be traded off for speed to produce equal latencies; at least a partial compromise between speed and accuracy would be expected, especially when, as in the present experiments, speed and accuracy are equally stressed in the instructions. Third, it might be argued that accuracy is traded off for speed to produce latencies that tend to cluster around a single point, but surely it cannot be argued that accuracy is traded off for speed to produce latencies that tend to cluster around three or more points. The latencies for list length 4 in Experiment 1, for example, are not equal; there are three levels, one for each value of the study position of the later probe. If the "true" latency (i.e., the latency uncontaminated by speed-accuracy tradeoffs) on a particular trial were midway between the bottom two functions in the left panel of Figure 2, how could the system trade off one way, to obtain a slower latency, if the study position of the later item were 3, and another way, to obtain a faster latency, if the study position of the later probe were 4?
Some of the proposals described in the introduction assume exhaustive processing of the probes and predict an effect on latency of the study position of the earlier probe. These models assert that the recency of each probe is determined and that these recencies are then compared. Such models would predict an effect of the study position of the earlier probe for one of two reasons. First, the earlier probe would be fully processed, and it is reasonable to expect that time to process the earlier probe would be a function of its study position. Second, the difficulty of the comparison should vary with the study position of the earlier probe, and it is reasonable to expect that comparison time would be a function of the difficulty of the comparison. It is possible that these two effects coexist and completely offset each other, but it is always unattractive to argue for offsetting processes to account for flatness, and it is especially unattractive when the flatness is as persistent as it is in the present experiments. (The few deviations from flatness that were obtained were not those predicted by either of the potentially offsetting processes.)
If exhaustive processing of the probes is ruled out, then the time-tag view may also be dismissed. Presumably time tags for both probes would have to be consulted before a recency discrimination could be made.
The present results are also incompatible with the possibility of a self-terminating forward scan of the memory traces, suggested by some data of Sternberg (1969, Experiment 8). That experiment was not a judgment of recency experiment, but it bore some resemblances to the present experiments. Sternberg presented two test words that had been in temporally adjacent study positions and asked subjects to report whether the test words were in the same order as in the study phase. Latency was a linear function of list length and was slower for later study positions. Those results suggest a process similar to that assumed by the conveyor-belt model, but with a forward scan instead of a backward scan. Such a forward scan is clearly ruled out for the present situation of discrimination of recency. The critical difference between the present task and Sternberg's task may be that he presented the study list twice and the subject recalled the list between presentations. Thus subjects were tested on the order of a learned list, whereas in the present experiments they were asked about the recencies of particular events.
The present data are consistent with several models that posit parallel self-terminating processing of the probes. (Rapid alternation between processing of the two probes is not precluded, as "parallel" is defined here; what is precluded is determining the recency of one probe before starting to determine the recency of the other.) According to the conveyor-belt version, parallel backward scans along the conveyor belt are initiated, and when a match for either probe is found, the scan terminates, rendering the position of the earlier item on the conveyor belt irrelevant to latency. The probe for which a match is found is selected as being more recent. Scanning takes time; therefore latency is a function of the study position of the later probe. Strictly speaking, the conveyor-belt model predicts a linear increase in latency with the lag of the more recent item, and the effects obtained in all four experiments are nonlinear. The deviations from linearity could conceivably be due to speed-accuracy tradeoffs. (Noneof the three problems with the earlier argument of speed-accuracy trade-off applies here.)
Normally, for recency discrimination tasks, exhaustive processing of the probes has been an assumption of strength theory (Morton, 1968) and attribute theory (Bower, 1972), and therefore these versions of strength theory and attribute theory are incompatible with the present data. But strength theory and attribute theory can be reconciled with the present data if parallel self-terminating processing of the probes is assumed, and if it is assumed that the rate of assessing strength or counting marked attributes is a function of strength or the number of marked attributes, respectively. According to a strength version of parallel self-terminating processing, at the time of test, the two memory traces are accessed directly and their strengths are assessed in parallel. Assessed strength accumulates gradually for each item until one reaches a criterion, at which point the assessment stops, rendering the strength of the earlier item irrelevant to latency. The item whose assessed strength reaches the criterion is selected as being more recent. Trace strength is a function of lag, and the rate of buildup of assessed strength is slower for weaker traces. The latter two assumptions make it possible for the system to discriminate the recencies, and also predict the effect on latency of the study position of the later probe. The attribute version would be similar to the strength view, but instead of strength being assessed, marked attributes would be counted.
In conclusion, the present experiments have shown that the time required to perform a recency discrimination depends on the recency of the later item but not on the recency of the earlier item. These data strongly suggest that processing of the test items is parallel and self-terminating, not exhaustive. With respect to the question of how recency information is coded and retrieved, the present data are compatible with strength theory, attribute theory, and the conveyor-belt model, and they are incompatible with time-tag views and withthe idea of forward self-terminating scanning of the memory traces.
References
Berlyne, D. E. Effects of spatial order and interitem interval on recall of temporal order. Psychonomic Science, 1966, 6, 375-376.
Bower, G. H. Stimulus-sampling theory of encoding variability. In A. W. Melton & E. Martin (Eds.), Coding Processes in human memory. Washington, D.C.: V. H. Winston, 1972.
Guyau, J. M. La genese de l'idee de temps (2nd ed.). In P. Fraisse, The psychology of time (J. Leith, trans.). New York: Harper & Row, 1963. (Originally published, 1902.)
Hinrichs, J. A. A two-process memory-strength theory for judgment of recency. Psychological Review, 1970, 77, 223-233.
Kirk, R. E. Experimental design: Procedures for the behavioral sciences. Belmont, Calif.: Brooks/ Cole, 1968.
Konorski, J. The physiological approach to the problem of recent memory. In J. F. Delafresnaye (Ed.), Brain mechanisms and learning. London: Oxford University Press, 1961.
Lipps, T. Grundtatsachen des seelenlebens. In P. Fraisse, The psychology of time (J. Leith, trans.). New York: Harper & Row, 1963. (Originally published, 1883.)
Morton, J. Repeated items and decay in memory. Psychonomic Science, 1968, 10, 219-220.
Murdock, B. B., Jr. Short-term memory. In G. H. Bower (Ed.), The psychology of learning and motivation: Advances in research and theory (Vol. 5). New York: Academic Press, 1972.
Murdock, B. B., Jr. Human memory: Theory and data. Potomac, Md.: Erlbaum, 1974.
Murdock, B. B., Jr., & Anderson, R. E. Encoding, storage and retrieval of item information. In R. L. Solso (Ed.), Theories in cognitive psychology: the Loyola symposium. Hillsdale, N.J.: Erlbaum, 1975.
Peterson, L. R. Search and judgment in memory. In B. Kleinmuntz (Ed.), Concepts and the structure of memory. New York: Wiley, 1967.
Postman, L. Does interference theory predict too much forgetting? Journal of Verbal Learning and Verbal Behavior, 1963, 2, 40-4.
Sternberg, S. Memory-scanning: Mental processes revealed by reaction-time experiments. American Scientist, 1969, 57, 421-457.
Wickelgren, W. A. Single-trace fragility theory of memory dynamics. Memory & Cognition, 1974, 2, 775-780.
Yntema, D. B., & Trask, F. P. Recall as a search process. Journal of Verbal Learning and Verbal Behavior, 1963, 2, 65-74.
This research was supported by Research Grant APA 146 from the National Research Council of Canada and Research Grant OMHF 164 from the Ontario Mental Health Foundation to Bennet B. Murdock, Jr., and by a National Research Council Postgraduate Scholarship. The author is grateful to G. S. Dell, J. E. Eich, A. J. Flexser, W. E. Hockley, and especially to Roger Ratcliff for useful comments, to H. L. Kaplan for his operating system, and to B. B. Murdock, Jr., for frequent help and encouragement.
Requests for reprints should be sent to Paul Muter, Department of Psychology, University of Toronto, Toronto, Ontario, Canada M5S 3G3.
Received July 27, 1978
Revision received September 28, 1978






