
This article presents a tentative theoretical framework for the study of asymmetry in the context of human bimanual action. It is emphasized that in humans most skilled manual activities involve two hands playing different roles, a fact that has been often overlooked in the experimental study of human manual lateralization. As an alternative to the current concepts of manual preference and manual superiority, whose relevance is limited to the particular case of unimanual actions, the more general concept of lateral preference is proposed, to denote preference for one of the two possible ways of assigning two roles to two hands. A simple model describing intermanual division of labor in the variety of human skilled manual activities is outlined. The two main assumptions of the model are the following. 1) The two hands represent two motors, that is, devices serving to create motion, whose internal (biomechanical and physiological) complexity is ignored in the suggested approach. 2) In humans, the two manual motors cooperate with one another as if they were assembled in series, thereby forming a kinematic chain: In right-handers allowed to follow their lateral preferences, motion produced by the right hand tends to articulate with motion produced by the left. It is suggested that the kinematic chain model may help in understanding the adaptive advantage of human manual specialization.
Functional asymmetry, human laterality, handedness, manual specialization, hand preference, two-handed movement, bimanual movement, gestures, human action, movement, kinematic chain model, global vs. local, micro vs. macro, hierarchical control.
This work has its origin in a one-year stay (1984-1985) at the Department of Experimental Psychology of the University of Oxford, jointly supported by the Royal Society and the Centre National de la Recherche Scientifique in application of the European Science Exchange Program. It received partial support from the Ministère de l'Industrie et de la Recherche (Grant no. 84 C 1308). I wish to thank members of the Department of Experimental Psychology for their friendly reception, and A. Allport, D. Broadbent, P. McLeod, and M. Treisman for helpful discussions.
Introduction
As regards the involvement of the left and right hands, the wide variety of human everyday manual activities falls into three classes: Some obviously asymmetric activities can be termed as unimanual (e.g., dart throwing, or brushing one's teeth); other activities are also markedly asymmetric but bimanual (think of differentiated bimanual activities such as dealing cards or playing a stringed musical instrument); and finally, there are activities that must be termed bimanual and symmetric, as the two hands play essentially the same role, either in phase (as in rope skipping or weigh/lifting) or out of phase (as in rope climbing).
These three classes of real-life human manual activities have received far from equal attention from psychologists, as is obvious when one considers the kinds of movements subjects are required to perform in usual laboratory tasks. There has been an early and sustained interest in unimanual movements, both on the part of the students of the basic mechanisms of motor control (Woodworth, 1899; Fitts, 1954; Schmidt, Zelaznik, Hawkins, Frank, & Quinn, 1979; Meyer, Smith, & Wright, 1982) and on the part of students of manual lateralization (see Porac & Coren, 1981, and Annett, 1985, for reviews).
Bimanual movements have only recently become popular among experimental psychologists interested in the problems of motor coordination and timing (Kelso, Southard, & Goodman, 1979; Kugler, Kelso, & Turvey, 1980; Turvey, Rosenblum, Kugler, & Schmidt, 1986; Wing, 1982). But it is interesting to note that, in this research trend, tasks have generally consisted of performing analogous or even identical movements with the left and right hands (for example, both hands act as pointers in Kelso et al.,1979, and they both act as oscillators in Turvey et al., 1986). Few investigators, apparently, have tried to understand what happens in bimanual activities that are inherently asymmetric in the sense that they demand two qualitatively differentiated manual contributions (Schönen, 1977; Ibbotson & Morton, 1981; Peters, 1981, 1983, 1985; Guiard, 1986, 1987a).
A plausible reason for this apparent lack of interest is that bimanual asymmetric activities appear to be more complex than activities belonging to the other two classes, as they combine problems raised by lateral asymmetry with problems raised by motor coordination. Unfortunately, however, it is unlikely that knowledge about the former issue can be combined with knowledge about the latter, as the study of bimanual asymmetrical activities appears to raise entirely new problems.
Specific Problems in the Study of Human Bimanual Differentiated Activities
The problem of asymmetry in the context of bimanual involvement. Let us consider, first, the problem of lateral asymmetry as it must be formulated in the context of bimanual gestures. If we think of a violinist, for example, it is rather obvious that neither of his or her two hands is dominant in any clear sense: Each of the two manual roles (grossly speaking, manipulating the violin, manipulating the bow) is crucial and difficult. To deal with laterality in the context of bimanual differentiated tasks, one definitely cannot resort to the current notion of hand preference, for the simple reason that no hand can be excluded from the task. At the same time, it would be arbitrary to say that these two roles differ in difficulty (Oldfield, 1969).
What we need actually is a concept of preference compatible with the fact that in a task consisting of two differentiated manual roles, A and B, there are two possible ways to assign role A and role B to the left and right hands (A-left and B-right, or A-right and B-left). Let us simply term as a lateral preference as distinct from manual preference the preference manifested by an individual in the face of two possible assignments of two roles to two hands in a task. It is important to remark that lateral preference, as just defined, represents a more general concept than manual preference: The reason that the former subsumes the latter is that a unimanual task can be thought of as a limiting case of a bimanual task, while the inverse is not true. More specifically, provided that we retain the possibility of one of the two manual roles being empty, we may legitimately consider that any asymmetrical task (whether obviously bimanual or supposedly unimanual) demands a choice between two possible role-hand assignments. Thus, for example, it would seem odd but would still be logically acceptable to say that in acts like throwing a dart or brushing one's teeth there are two roles to be assigned to two hands, one of which seemingly consists of just doing nothing. This view amounts to dropping the unimanual-bimanual distinctionwhich cannot be stated with sufficient clarity, as will be shown belowand eventually retaining a single dichotomous criterion for the classification of manual activities with respect to laterality: The two hands do or do not play the same roles; that is to say, there is symmetry or asymmetry.
There are two main justifications for so incorporating, a priori, all asymmetrical manual activities into the bimanual class. First, for any task in which only one hand seems to be involved, it is impossible to demonstrate that the other hand plays no role. For example, the possibility inevitably exists that in dart throwing the hand that neither grasps nor throws the dart contributes some postural or any other non identified function to performance. In case of uncertainty as regards the existence of a second manual role, one takes a risk in deciding that action is unimanual, as can be illustrated with the example of handwriting. Although the current view that handwriting represents a unimanual activity is convenient in the study of this skill (e.g., Hollerbach, 1980; Wing, 1978), it is interesting, in the light of the present discussion, to note that this view is demonstrably incorrect: Under standard conditions, the spontaneous writing speed of adults is reduced by some 20% when instructions prevent the non-preferred hand from manipulating the page (Athènes, 1984). This is evidence that a second manual role does exist in handwriting (Guiard & Athènes, 1985; Guiard & Millerat, 1984).
The second justification is less formal, and perhaps also more serious, having to do with the general intelligibility of human manual lateralization. It is arguable that the lack of interest so far manifested by experimental psychology with regard to the very large class of human gestures that involve two well differentiated manual roles has to do with the fact that psychologists have in general reasoned on the basis of too reductive a paradigm, namely that of the forced choice between the left and the right hands. Notwithstanding the value of such an approach, which has placed investigators in a position to successfully cope with the puzzling problem of human between-individual variability (right- versus left- or mixed-handedness, see Annett, 1985), it must be realized that thinking exclusively in terms of the between-hand forced choice paradigm has had the substantial cost of rendering the problem of asymmetry in bimanual gestures intractable.
Provided that one now forgets about interindividual differences and
chooses to focus upon the typical, albeit non universal, case of right-handed
humans, there is room for trying to incorporate more complexity into one's
representation of human manual lateralization. What then must be acknowledged
is that, in general, the asymmetry characterizing the manual gestures of
humans reflects the assignment of different roles to two hands, rather
than a preference for one hand, the latter phenomenon being observable
only in the very particular, and always disputable, case of unimanual tasks.
The problem of bimanual coordination in the context of asymmetry.
Just as the problem of asymmetry must be posed in different terms when
bimanual, rather than unimanual, tasks are considered, the problem of bimanual
coordination must be posed in different terms when asymmetric, rather than
symmetric, tasks are considered. One obviously cannot compare bimanual
coordination as it manifests itself in gestures made up of two qualitatively
differentiated manual contributions to what happens in experimental tasks
requiring the two hands to behave like two essentially interchangeable
machines (Kelso, et al., 1979; Kugler, et al.,1980; Turvey, et al., 1986;
Wing, 1982). In fact, the very question of how the left and the right hands
coordinate their efforts in differentiated gestures cannot be adequately
approached until one has some idea about how the two hands cooperate with
each other to produce an integrated output. In other words, the question
of the relationship between the sub-tasks, or roles, assigned to the left
and the right hands, that is, the differentiated logic of division of labor
between the two hands, should be our first concern.
Intrinsic Importance of Differentiated Bimanual Gestures in the
Behavioral Repertoire of Humans
One sufficient reason to regret that differentiated bimanual activities have been neglected so far in the study of human laterality is that these activities are liable to have played a critical role in-the adaptation of humans to their natural environment, and even perhaps in the very process of hominization. The privileged intrinsic importance of these gestures, as compared to unimanual and to bimanual symmetrical gestures, is suggested by two converging considerations, one quantitative and the other qualitative.
First, although it has been a tradition in the area of human laterality to favor the study of supposedly unimanual acts due to the current belief than human skills reside in the special capabilities of the so-called dominant hand it is important to realize that certainly a vast majority of human manual acts of real life belong to the bimanual asymmetric class. Not only is it quite obvious that asymmetry is the rule and symmetry the exception, but there is also little risk in saying that most asymmetrical manual activities involve the two hands.
To justify this statement in the absence of any available extensive definition of the real repertoire of human manual activities, let us examine the composition of current handedness questionnaires, which consist of samples drawn from this repertoire. Questionnaires on hand preference happen to quite systematically include a proportion of questions relating to admittedly bimanual actions, such as dealing cards or threading a needed (e.g., Annett, 1967; Oldfield, 1971; Briggs & Nebes, 1975; Bryden, 1977; Provins, Milner, & Kerr, 1982; Beukelaar & Kroonenberg, 1983), a puzzling fact at first sight since, for such acts, no preference for any hand can be at least directly assessed.
In fact, in typical questionnaires, questions bearing on acts explicitly held as bimanual even represent the majority of the items. Thus, of Annett's (1967) eight items, five refer to bimanual acts (sweeping, shoveling, striking a match, using scissors, and threading a needle) and only three to conceivably unimanual ones (writing, drawing, throwing). In the longer, 12-item questionnaire later designed by the same author (Annett, 1970), there are 7 bimanual items (dealing cards, unscrewing a jar, shoveling, sweeping, threading a needle, striking a match, and using scissors), 2 items that cannot be classified in this respect for lack of a sufficiently precise evocation of the task context (hammering and using a racket), and only 3 arguably unimanual items (writing, throwing, and using a toothbrush). In Oldfield's (1971) most popular questionnaire, the picture is not different with bimanual items again representing the absolute majority (11 items out of 20) and unimanual ones representing just a small minority (5 items). As for the very wide-ranging hand preference questionnaires such as the 51-item questionnaire of Beukelaar and Kroonenberg (1983) or the 75-item questionnaire of Provins et al. (1982), their composition demonstrates even more clearly that there is, in the population of human everyday activities, a shortage of instances of unimanual tasks relevant to the study of manual preference and an abundance of instances of bimanual tasks.
We come to the second, qualitative, argument for believing that bimanual differentiated activities are of considerable intrinsic importance in humans. There seems to be no indication that a humans preferred hand, as compared to a non-human primate's hand, has any species-specific basic motor abilities. Insofar as elementary unimanual movement capabilities are considered, as in laboratory aiming tasks of various difficulty, it is feasible for students of motor processes to replace human subjects with monkeys, with the latter producing, after appropriate training, performances quite comparable to those of humans for speed and accuracy. For example, Requin and his colleagues, studying motor preparation in an aiming task requiring monoarticular rotation at the wrist, ran much the same experiments and collected similar reaction time and movement time data in parallel in human subjects (Lépine & Requin, 1983) and in rhesus monkeys wearing intra-cranial microelectrodes (Riehle & Requin, 1986). The outstanding manipulative abilities of humans can certainly not be understood at such an elementary level of analysis. What is really specific to humans, as opposed to their primate cognates, is their ability to conceive of and execute manual gestures implementing a huge variety of actions. It is likely that the emergence of the human ability to appoint their two hands to well defined complementary roles, that is, to solve motor problems with bimanual asymmetrical gestures, has represented an important step in the process of hominization.
Scope of the Present Approach
The approach to the study of human manual asymmetry that will be sketched here does not follow to this writer's knowledge any firmly established scientific tradition. It seems necessary therefore to make explicit in what sense it represents a departure from current thinking in the field.
A first decision in this approach is to treat human manual laterality in a purely within-individual perspective, considering the case of right-handed people only. It has been a tradition in the psychology of human laterality to place high priority on the intriguing fact that, although most humans are right-handed, far from all are. In this sense, it is arguable that most of what has been done in this area belongs to differential psychology, with the central concept of handedness representing basically a between-individual variable, as the different values of handedness correspond to different individuals. The present approach is based on an alternative, complementary strategy consisting of an attempt to grasp the relationship that the two hands of an individual bear to one another in action, it being understood that this basic rather than differential research perspective renders the problem of between-individual variability, at least temporally, intractable. Therefore, we shall here exclusively consider the case of right-handedness a rather typical case in humans after all and we shall deliberately ignore the problem of handedness stricto sensu.
A second decision is to adopt a resolutely behavioral approach, that is, to refrain from resorting to hemispheric or, more generally, neuropsychological interpretations. Not denying that neuroscientists have much to offer to the study of asymmetric manual behavior, I believe that the psychology of human normal laterality can do more than merely look for behavioral signs or symptoms of the functional organization of the central nervous system. For example, Kimura's (1961) seminal work on auditory laterality effects and her more recent studies on asymmetry of spontaneous manual gestures during speaking and various cognitive activities (Kimura, 1973; Kimura & Humphrys, 1981; Hampson & Kimura, 1984) represent exemplary attempts to test hypotheses on the brain (see Kimura & Archibald, 1984; Kimura, 1982). Thus, although the findings put forward, such as the right-ear advantage in dichotic listening, or the higher probability of making free gestures with the right than left hand during speaking, do represent relevant neuropsychological evidence, they definitely fail to make sense at a strictly behavioral level. In contrast, we shall try to identify facts and principles regarding manual asymmetry that will help to understand this phenomenon per se.
One may suspect that the reason why no satisfactory synthesis has been up to now accessible between the functional asymmetry of the brain and asymmetry of manual behavior is that there has been insufficient theoretical elaborations of the latter issue by psychologists. Basically two positions have been advocated, since Broca (1865), as regards the hypothetical relationship between hemispheric functional lateralization and hand use asymmetry.
According to one position, consistent with Broca's, and characterized by a marked emphasis on the importance of language, left-hemispheric dominance for language and right-hand dominance for manual skill represent, in the final analysis, two facets of one and the same brain lateralization phenomenon (e.g., Kimura, 1982; Calvin, 1982; MacNeilage, Studdert-Kennedy, & Lindblom, 1984; Tzeng & Wang, 1984; Annett, 1967, 1985). To use Annett's word, this position reconciles "brainedness" with handedness, at the expense, however, of ignoring that the right hemisphere too has its functional specialization (Brain, 1941; Nebes, 1971; Newcombe, 1969).
The alternative position, based on the assumption that there is complementarity of function between the two hemispheres of the brain, but not between the two hands in motor behavior (no hemisphere is dominant overall, but the right hand is), leads to the view that the two lateralization phenomena under consideration are mutually irreducible (Hécaen & Ajuriaguerra, 1964; Satz, 1979; Porac & Coren, 1981; Bryden, 1982). When the cooperative organization of human asymmetrical bimanual gestures is better understood, one will perhaps be able to build, between cerebral functional asymmetry and asymmetry of hand utilization, a bridge that will help theorizing on both sides.
So long as one-handed acts are considered, the description of asymmetry is simple, requiring a single, possibly quantitative, variable. The asymmetry characterizing one-handed acts can be reduced to a simple quantitative difference between the left and the right hands, in terms of frequency of use (manual preference) or in terms of performance proficiency (manual superiority). With bimanual differentiated acts, asymmetry becomes much more obvious (no observer might reasonably doubt that the two hands do different jobs in activities such as dealing cards or playing the guitar), but at the same time the phenomenon seems more difficult to grasp, being no longer amenable to any simple description because the nonidentity of the left and right actions results from an indefinite number of lateral differences. In this section, I shall try to define three high-order principles that appear to determine the asymmetry of human bimanual gestures in a fairly regular fashion, and which any theory of manual lateralization, I believe, should take into consideration.
Right-to-Left Spatial Reference in Manual Motion
The first of these principles is that in human real-life gestures, motion of the right hand typically finds its spatial references in the results of motion of the left hand. To illustrate this, let us first examine the case of movements where the left hand plays a postural role in keeping an object steady while the right executes a manipulative action on it, a case often thought to represent a prototype of human bimanual differentiated movements (e.g., Byron, 1948; Schönen, 1977; Peters, 1983; MacNeilage et al.,1984). There is little doubt that in gestures of this kind, the left hand contributes an important stabilizing action to the achievement of the global act: For example, in sewing, no accurate activity could be performed by the hand carrying the needle if the fabric were not kept steady. However, to say that the left hand offers stability in such a context is insufficient. Unlike a clamp, the postural hand ensures plastic stabilization, that is, produces steady states that are subject to frequent alterations thanks to which the position and the orientation of the fabric always remain appropriate to the action of the right hand. In other words, it would be fallacious, in situations where the left hand is appointed to a postural role, to conceive of the between-role differentiation in terms of a stationary left hand and a mobile right hand, because mobility is to be found undoubtedly on both sides. What we want to understand, rather, is the relationship between motion produced by the left hand and motion produced by the right.
The fact that in the category of bimanual differentiated gestures evoked here the motor activity of the left hand serves the function of defining steady states, while that of the right typically creates changes, is an invitation to think that the right hand finds its spatial references in the product of the activity of the left. To use the terms of MacNeilage et al., (1984), we may say that the left hand delineates "frames" into which the activity of the right hand inserts "contents." It is important to recall that no movement can be thought of without a spatial reference. In a manual gesture consisting of the coordination of stabilization and manipulation, it is clearly with reference to the temporary steady positions defined by the stabilizing hand that the manipulative hand organizes its action. Thus, in embroidery, the loops followed by the needle have their targets in the pattern drawn on the fabric: As the orientation and the position of the fabric are highly changeable, being periodically revised by the left hand, it would be vain to try to evaluate the performance accuracy of the right hand from the recording of its movements relative to the general environment.
A very simple experiment on handwriting can illustrate the right-to-left reference principle quite clearly (see Figure 1). Skilled handwriters were asked to fill out a sheet of paper on dictation while leaning on a specially prepared desk blotter that hid a sheet of carbon paper. With this device, two recordings could be obtained of the same handwriting movement, one intentional on the sheet of paper and the other unintentional on the surface of the table. As illustrated by the example reproduced in Figure 1, the two obtained recordings were markedly different. This was simply because, as is usually the case in normal handwriting, the sheet of paper had been periodically re-positioned during the writing process. The fact that in such an experiment the writing trace left on the surface of the table is severely disorganized shows straightforwardly that motion of the pen is executed, not with reference to the environment, but with reference to landmarks located on the sheet of paper, a mobile object manipulated by the non-preferred hand (Guiard & Athènes, 1985; Guiard & Millerat, 1984).
With the examples of sewing and handwriting, we have so far examined the problem of the spatial references of manual motion in the particular case of bimanual gestures comprising a stabilization and a manipulation component. The question then arises whether the principle of right-to-left reference still holds in other categories of bimanual differentiated gestures where the left hand produces no steady states and cannot be considered to play a stabilization role. Note that there is no logical inconsistency in imagining that a moving hand may offer a spatial reference for the motion of the other hand, since obviously motion and stationarity are relative notions: If I am walking along the corridor of a train carriage, I shall refer to the same fixed landmarks in this local space whether the train is immobile at a station or running on the railway at a high speed. Likewise, one need not assume that the left hand adopts immobile postures to ask whether the right hand elaborates its motion relative to it.

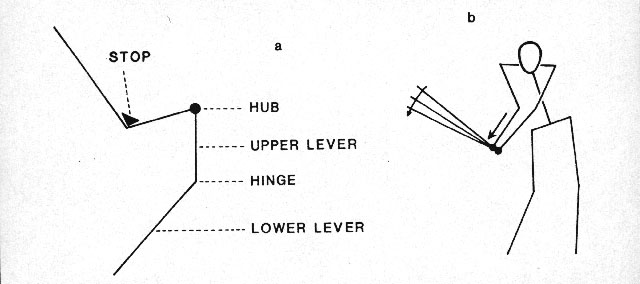
To define the role of the left and the right hands in this kind of hitting movement, we may rely on Cochran and Stobbs' (1968) classic analysis of the golfer's swing. These physicists have convincingly shown that a golfer can be compared to a two-lever system working in a single plane (see Figure 2): The upper lever corresponds to the two arms rotating about a virtual "hub" located somewhere between the two shoulders; the lower lever corresponds to the club itself, rotating about the extremity of its handle. Cochran and Stobbs make it clear that the left, backhand arm is the master in the control of the acceleration of the upper lever, while it is the right, forehand arm that controls the acceleration of the lower lever shortly before impact, a view consistent with that of many golf professionals (e.g., Connelly, 1984; Nicklaus, 1983). From this we may conclude that the action of the right hand in a golf swing consists of controlling rotatory motion with reference to an angular position controlled by the left hand, the latter position being also variable during the swing. With other implements such as those listed in the last paragraph, the orientation of the rotation plane, the amplitude of the rotation, and other aspects may differ, but, for physical reasons made obvious by Cochran and Stobbs, the two-lever model is likely to remain valid. An important observation in this respect is that apparently all long implements designed for hitting with a rotatory movement are preferentially handled by right-handers with a grip analogous to that displayed by golfers, that is, with the left hand positioned at the top of the handle (Guiard, 1987a). Thus it seems that the principle of right-to-left spatial reference governs human asymmetrical bimanual gestures, irrespective of whether the left hand has the responsibility of producing steady states or motion.
We have seen that immobilization of the left hand during bimanual differentiated action is not a prerequisite for this hand to offer a spatial reference to the elaboration of right hand motion, because motion and stationarity are relative. There is a limit to this relativity, however, in the sense that motion of an object can only be produced and interpreted with reference to another mobile object provided that the mobility of the latter inscribes itself in a larger scale of time and space.
Let us consider the case of gestures consisting of a left postural and a right manipulative component, taking again handwriting as an example. The reason that, from the point of view of right hand action, the position of the page can be used as a spatial reference even though the page is subject to periodical motion is that the mobility of the page takes place at a definitely larger temporal and spatial scale: Compared to the motion of the pen tip in the page, the motion of the page on the table is characterized by a low temporal frequency (comparatively long periods) and by a low spatial frequency (comparatively large movement amplitudes).
It is a commonplace to say that the right hand is capable of producing finer movements than the left, and this has been shown to be true both for tasks measuring accuracy of timing such as finger tapping tasks (e.g., Peters, 1980) and for tasks measuring spatial accuracy such as aiming tasks (e.g., Flowers, 1975; Todor & Kyprie, 1980). The point made here is that the different capabilities of the two hands for resolution of movements may well have to do with their more or less permanent involvement in different temporal-spatial scales of motion. Considering the vast repertoire of bimanual activities of real life in which the left hand receives a postural role, there appears to be a fairly systematic contrast between the two manual roles such that the right hand can be said to typically exhibit a finer temporal resolution and a finer spatial resolution. In other words, the suggestion is that the left and the right hands might be more faithfully labeled macrometric and micrometric, respectively, rather than unskilled and skilled.
One strong argument for hypothesizing a scale contrast between the two hands in bimanual differentiated gestures rests on Webers law applied to the production of movement. As shown a century ago by Stevens (1886, cited by Wing, 1986) and confirmed recently (Schmidt, Zelaznik, Hawkins, Frank, & Quinn, 1979), there is approximate proportionality between the standard deviation and the mean of movement time (or period) in temporal interval reproduction tasks. This implies that for a given motor system of limited capacity an increase in the temporal resolution of movement can only be obtained at the expense of a reduction in movement time. Much the same approximate proportionality holds between the standard deviation and the mean of movement amplitude in spatial interval reproduction tasks (Schmidt, et al. 1979), leading, for space, to the same implication as regards the relationship between fineness of resolution and magnitude.
The main difference between the concept of a macrometric-micrometric (or scale) contrast between the left and the right hands and the traditional view that the right hand is globally superior to the left lies in the assumption that there is complementarity of function between the two hands, with their specializations representing opposite compromises with respect to the resolution-magnitude tradeoff dictated by Webers law. With this view in mind, there is no necessity to assume superiority of one hand over the other, just as there is no necessity to assume superiority of a micrometric vernier over a macrometric one on a device serving on a microscope to set the distance from the lenses to the studied section. There is no necessity to reject the possibility that the right hand is superior to the left either, as the Weber fraction may differ. The point, simply, is that the unequal abilities of the two hands to perform high resolution movements is liable to be due, at least in part, to their different specialization in real life as regards scale of movements.
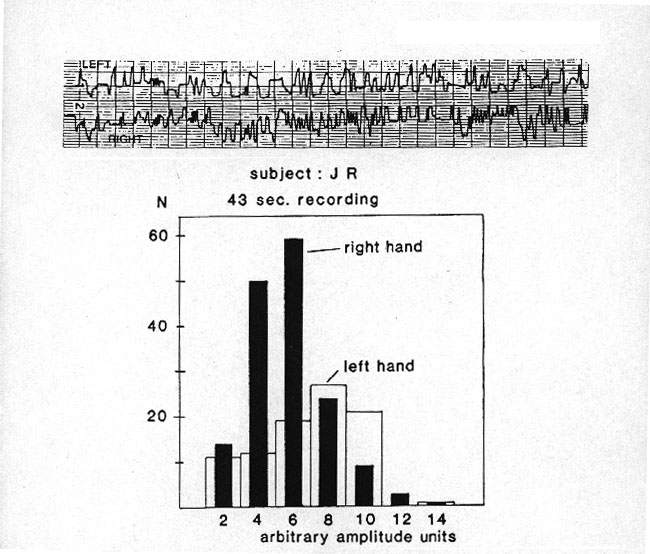
The report of an unpublished, recently run, experiment may be relevant here. Right-handed subjects were requested to produce random motion on the screen of a CRT, by manipulating a pair of potentiometric knobs with the two hands, one of which controlled the vertical position and the other the horizontal position of the spot. With the two knobs subjects were asked to impart motion to the spot in such a way as to have it move, within a prescribed square, as unpredictably as possible (to another person watching the screen), both from a spatial and a temporal point of view (irregular spatial trajectories, irregular speeds). A polygraph served to record the motion produced at the two knobs, on separate tracks.
The upper part of Figure 3 presents the activities of the left and right hands recorded for a 43-s period in a representative subject. It is clearly apparent that more energy was expended by the right than by the left hand in high frequencies. Thus, in a bimanual task where each hand was free to produce oscillations compatible with its preferred frequency band, it was confirmed that the subjects spontaneously displayed shorter periods with their right than left hand, presumably without being aware of the asymmetry. But this is, apparently, only half of the story. It turned out that not only did the right hand cycles present shorter time periods, they also had smaller amplitudes, as illustrated in the lower part of Figure 3. The histogram represents for each hand the distribution of the amplitudes of the oscillations, estimated on raw recordings by merely measuring peak-to-peak vertical distances. As is visible in the histogram and to some extent in the raw data the right hand generally produced smaller movements than did the left (c² = 23.43, p < .001, median test). The fact that the sum of the peak-to-peak amplitude measures over the common working period was greater for the right than left hand (834 vs. 565 arbitrary units in this sample) means that certainly more energy was expended by the subject with the right hand than with the left, a phenomenon that might have to do with manual preference. It remains, however, that the right hand tended to produce oscillations that not only were faster than those of the left (shorter movement times) but also covered smaller amplitudes. The association of these two differences makes sense if it is assumed that the two hands are specialized for working at different levels of scale.
Left-Hand Precedence in Action
The third important principle that appears to hold for a wide variety of two-handed human gestures in real life is that the left hands contribution to current action starts earlier than that of the right. We shall again consider in turn gestures presenting a postural-manipulative division of labor, where this principle seems to be obviously verified, and gestures requiring a dynamic contribution on the part of the two hands.
In gestures like handwriting, sewing, driving a screw, and so forth, it would make no sense to start the manipulative action with the right hand before the object supporting this action has been adequately positioned and oriented with the left. Before handwriting starts, the page must have been moved to the area that the right hand will be able to reach with the least effort, and so oriented that with a simple rotation of the forearm the pen will produce a good approximation of horizontality in the page; in sewing the fabric must have been brought to a position and an orientation compatible with the privileged plane in which the loops of the needle will be formed; the screw must have been inserted into the hole, and so forth. More generally, postural adjustments are known to precede the execution of movements (e.g., Belen'kii, Gurfinkel', & Pal'tsev, 1967).
One partial reason that in bimanual gestures of the postural-manipulative kind the right hand is recruited with a delay is that for the manipulation proper to start, the object must be fixed in place. More importantly perhaps, the left-hand precedence principle has to do with the two principles evoked in the preceding sections, calling upon the principle of global precedence familiar to students of visual perception (e.g., Navon, 1977). Just as it seems logical that for an observer requested to identify a particular visual form, the information pertaining to the general contour of the form is usually gained earlier than that pertaining to its relatively high-frequency details, likewise it seems logical that action of the left hand, which represents the low-frequency component of a bimanual gesture and defines the spatial reference vital to the elaboration of motion of the right hand, intervenes first in time. We are apparently faced with quite a general hierarchy principle according to which human action, whether perceptual, intellectual, or motor, preferentially proceeds from the macro to the micro, that is, outlines global traits before delineating more detailed aspects.
The fact that in bimanual gestures involving no postural immobilization with one hand the left-hand precedence principle apparently still holds is an argument in favor of the view advocated here. Were immobilization of the manipulated object the reason for left-hand precedence in postural-manipulative bimanual gestures, we would expect that in other instances where the left hands contributes no stability to overall action the temporal order of the left and right manual recruitment would be random. In fact, it is a typical feature of bimanual dynamic action that the left hand is recruited first, as in the case of the golf swing, where, as noted above, the right hand copes with rotatory motion of the club about itself only toward the end of the downswing.
In this section I shall present a simple model, based on a non-quantitative physical approach, which aims at describing the logic of division of labor that appears to govern the variety of human bimanual asymmetrical actions. The model has the virtue of accounting simultaneously for the three principles examined in the preceding section: Namely, in general right-hand motion is built relative to left-hand motion, corresponds to a temporal-spatial scale that is comparatively micrometric, and intervenes later in the course of bimanual action.
The model has two basic constitutive assumptions: The first assumption likens the two hands to a pair of abstract motors. The second asserts that in humans these two motors tend to be assembled in series, thereby forming a kinematic chain.
The Hands as Abstract Motors
The way instances of bimanual gestures like handwriting and swinging a golf club were described in the foregoing may certainly be considered highly schematic, or superficial, as all the underlying biomechanical complexity was ignored. Thus, for handwriting, we examined motion of the pen and motion of the page, and, for the golf swing, we considered the rotatory motion of a pair of levers, not taking into consideration the fact that each of the two agents involved in such tasks was in reality a complex anatomical machine, a limb with many degrees of freedom controlled by many muscle ensembles. In brief, we have made use of a "hand" concept that may be judged rather unrealistic by those who wish to approach the study of bimanual movements from a physiological standpoint, particularly because in "bimanual" actions the two upper limbs, and not only the two hands, are involved.
In fact, it is a deliberate feature of the present approach to consider what must be done by the left and right hands (or upper limbs) to build up a bilateral gestural configuration, to the exclusion of how the joints and the muscles must be used. It is important to make explicit that the present study represents an attempt to understand bilateral cooperation in terms of the parameters of the task (the ends) rather than in terms of parameters of the anatomical organs (the means). This amounts to trying to identify regularities in the roles that are typically assigned to the left and to the right hands across the variety of bilateral asymmetrical tasks. Along these lines, it is legitimate to use the term hand to denote agents or actors in tasks that demand division of labor between them, it being understood that the term serves to globally label quite an elaborate anatomical device, the analysis of which is left to other investigators.
One slightly more formal manner of formulating this theoretical choice is to say that we regard the two hands as abstract motors, defining a motor as any natural or artificial device serving the function of creating motion. As for the word "abstract," it refers to the fact that no attempt will be made to take into account the internal mechanisms that make the motor work. Figure 5, which represents a motor as a black box, illustrates this point of view.
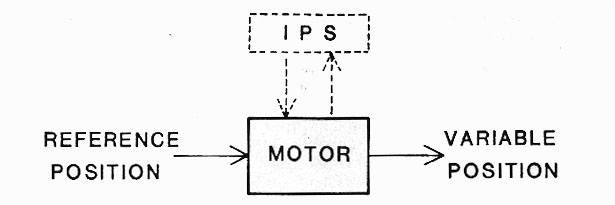
Figure 5 also represents a link between the motor and an information processing device, in the form of a pair of vertical pathways corresponding to afferences to and efferences from the device. If we think of a hand as a motor, we cannot deny that its functioning is placed under the responsibility of a vast ensemble of nervous structures ranging from the spinal to the cortical levels. However, just as it may be fruitful temporarily to ignore the internal constitution of a motor (joints and muscles in the case of a hand), it may also be fruitful temporarily to ignore the device responsible for its control (the nervous system). The main justification for this position is that, insofar as motor behavior is considered, the nervous system has presumably nothing more clever to do than trying to conform as accurately as possible to the task physics to produce adapted gestures in spite of the complexity of the skeletal structure (Bernstein, 1967; Kugler et al., 1980; Turvey, Shaw & Mace, 1978). In this perspective, it may have heuristic value to approach the study of bimanual cooperation by stressing for the time being the mechanics of the task (motion) rather than the biomechanics of the limbs (internal degrees of freedom) or information processing (nervous control).
Assembling Two Motors: Orthogonal, Parallel, and Serial Assemblies
Once the two hands have been likened to two abstract motors, the question arises of how these two motors can cooperate with each other to do effective work. This question may be conveniently reduced to the simpler question of how two motors can be assembled in order to produce a unitary mechanical effect. There appear to exist three ways of assembling two motors to form a cooperative structure: The motors can be assembled orthogonally, in parallel, or in series (see Figure 6).
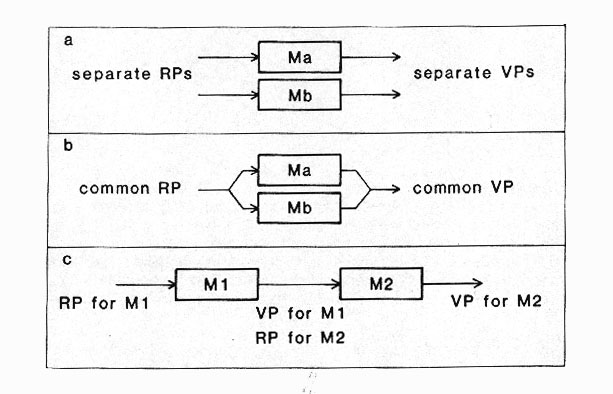
In a parallel assembly, the two motors act upon the same dimension of motion in a synergistic fashion, essentially adding non-differentiated contributions. Weightlifting in athletics is an example of a bimanual action based upon a parallel assembly of the two manual motors. A parallel assembly presents the property of mutual dependence between motion of the two motors, as expressed in the middle of Figure 6 by having the same reference position serve as a common input to the two motors and the same variable position represent their common output. This assembly also obeys a symmetrical logic of division of labor, as shown by the figure.
Finally, in a serial assembly, the two motors are required to work on the same dimension(s) of motion, but it is the output from one motor (M1) that serves as the input to the other (M2). Bimanual gestures such as handwriting or a golf swing, which we discussed above, are examples: The right hand moves the pen with reference to the page, which is manipulated relative to the table by the left hand; the right hand rotates the club (the lower lever in Cochran & Stobbs' [1968] terms) with reference to the angular position of the upper lever, with the latter being predominantly guided by action of the left hand. As depicted in the lower part of Figure 6, the system formed by two motors assembled in series receives a single input and yields a single output, as is the case with a parallel assembly; the two motors, however, can no longer be confounded, as they offer different contributions to overall performance because they occupy different ranks in the series (hence their ordinal indexing as M1 and M2, rather than Ma and Mb in nominal terms). A serial assembly of two motors has the property of partial dependence, in the sense that motion of M2 depends on (is calculated relative to) motion of M1 while the converse is not true, and obeys a logic of division of labor that is obviously asymmetrical.
Although the orthogonal assembly of two motors may serve as a model for some human bimanual gestures the instance of the operator of a milling machine invoked above presents a clear isomorphism it fails to apply to the general case because left-right independence is characteristic of few bimanual tasks carried out by humans. The parallel assembly model has also a limited scope because few human gestures exhibit the properties of mutual dependence and symmetry. As for the serial assembly of two motors, its property of asymmetrical division of labor makes it, in contrast, potentially suitable for modeling the way the two hands typically cooperate with one another in humans. This leads us to examine it more thoroughly.
The Kinematic Chain Model
When two or more motors are assembled in series, they form a kinematic chain, whose most common instance is an arm. Such a chain may be made up of a serial assembly of torque motors (e.g., an appendage), or linear motors (e.g., a telescopic arm), or a mixture of torque and linear motors (e.g., think of a pneumatic drill mounted at the end of an articulated chain). The view I wish to propose is that a speaking functional analogy exists between the way in which any two contiguous motors of a kinematic chain cooperate with each other and the way in which the left and the right hands cooperate with each other in human skilled gestures. This analogy, I believe, is interesting in that it offers the possibility to describe bimanual cooperation in terms of the simple system formed by a kinematic chain. To show that the kinematic chain may serve to model bimanual cooperation in human differentiated gestures, I will now try to make it clear that the three previously mentioned high-order principles that govern the functional relationship between the two hands in typical asymmetric gestures of humans also hold when two contiguous motors of a kinematic chain are considered.
Distal-to-proximal spatial reference. The first principle, right-to-left reference in manual motion, has its obvious analogue in any pair of contiguous motors in a kinematic chain: If motors are assembled in series, the principle that the output from any motor rank of n represents the input to the motor of rank n + 1 is true by construction. The only stipulation that must be added here to model the two hands as two contiguous motors in a chain is that we will compare the activity of the left hand to that of the motor of rank n (the more proximal of the two), and the activity of the right hand to that of the motor of rank n + 1 (the more distal of the two).
Proximal-distal contrast in the spatial-temporal scale of motion. The second principle, the left-right contrast in the temporal-spatial scale of motion, also has its straightforward cognate in a kinematic chain, the left and the right being replaced by ranks n and n + 1, respectively. To consider the temporal scale first, we may note that a motor occupying rank n in a concrete chain has a necessarily greater inertia than that occupying rank n + 1, simply because the former carries the latter. Thus, a monotonic inertial gradient from the most distal to the most proximal rank of a chain exists whatever the nature (torque versus linear) of the assembled motors.
Using his or her own arm a structure that can be described as the serial assembly of a number of torque motors the reader may quite easily verify that this inertial gradient results in a temporal frequency gradient, by producing free monoarticular oscillations at various joints in turn, keeping the angular amplitude of the oscillation approximately constant (say, 20° or 30°). Keeping the palm of the hand steady, one can oscillate one's middle finger as a whole at about 7 or 8 Hz; a perceptibly lower maximal frequency, about 6 Hz, will be reached with the whole extended hand oscillating about the wrist; the ensemble formed by the forearm and the hand will oscillate about the elbow at a still lower maximal frequency (about 5 Hz), and finally, the whole extended arm will hardly reach 4 Hz when oscillating about the shoulder. So the more distal the rank of a motor in a kinematic chain, the higher the temporal resolution of its potential contribution to the global motion of the chain.
As to the scale of motion taken now in a spatial sense, there appears to be quite a similar gradient along a kinematic chain: Again, the more distal a motor, the higher the spatial resolution of its potential contribution to overall performance. The reason, obviously, has to do with the unequal proportions contributed by motors occupying different ranks to the amplitude of overall movement that is, movement produced by the chain as a whole. To illustrate this, consider a simple aimed movement such as touching a point located at a distance on a table while seated. What the limb has to do here is to move its endpoint, the tip of the forefinger, from a home position to the target: Motion of this single endpoint thus represents the unitary end of the coordinated actions of all the torque motors appointed to their respective joints. Considering the length of the endpoint trajectory, there is little risk in saying that angular motion at the three joints of the forefinger accounts for a very small proportion of it, while angular motion at the elbow or the shoulder accounts for most of it.
In the evoked instance, the reason that these proportions differ is simply that, on the average, the more proximal a torque motor in a chain, the longer the radius of rotation (the moment arm) placed under its control, and therefore the larger the amplitude of motion induced at the endpoint of the chain by the same amount of angular motion. This geometric argument obviously fails to apply to a kinematic chain composed of linear motors. However, for logical reasons that should become clear in the following, a satisfactory serial assembly of linear motors should generally be one in which the linear run controlled by the component motors would be an inverse function of their rank, as is the case in optic microscopy, for example, with the macrometric and the micrometric knobs of the device controlling the linear distance between the section and the lenses: The knob that moves the other (i.e., the knob occupying the more proximal rank) is the one that controls the macrometric range.
In sum, we may view a kinematic chain as a hierarchical mechanical system
whose various elements tend to contribute to overall motion at different
scales of time and space, the temporal-spatial scale varying as an inverse
function of the rank in the chain. Therefore, we may conclude that any
two contiguous motors in a kinematic chain bear a relationship with one
another that resembles, as regards the temporal-spatial scale of motion,
the relationship existing between the left and the right hands in typical
human asymmetrical gestures.
Proximal precedence. The third principle, left-hand precedence in
action, also has its obvious analogue in the context of a kinematic chain,
in the form of a proximal precedence principle. Once it has been recognized
that in a structure composed of motors assembled in series, the ranks occupied
by the various motors differentiate the scale of their respective contributions,
with a lower (more proximal) rank corresponding to a lower level of spatial-temporal
resolution, it stands to reason that the more proximal a motor in the chain,
the earlier it is liable to be solicited in a given action of the chain.
The example of a simple arm movement aimed at touching a target with the
tip of the forefinger can serve again to illustrate this proximal-precedence
principle quite straightforwardly: It would make no sense, in an aiming
gesture large enough in amplitude to involve the more proximal joints of
the arm, to have the more distal joints start their own contribution before
the hand has been brought to a reasonably short distance from the target.
Practically, if the role of the three finger joints is to lower the forefinger
in order to rest its tip on the table at the target, these distal joints
will only come into action toward the end of the trajectory. The case of
the gesture consisting of reaching and grasping, extensively investigated
recently since Jeannerod (1981; see also Paillard & Beaubaton, 1978),
is worth considering in this respect. This gesture has been examined as
if the proximal action of reaching (moving the hand, mainly thanks to the
shoulder and the elbow) and the distal action of grasping (opening and
closing the finger grip) represented two equally long-lasting, and practically
contemporary actions, the relative timing of which must then be understood.
It is important to realize that the time courses of these two components
of the gesture have a different significance: Whereas the reaching component
represents the execution of a single transport action, the grasping component
is biphasic, consisting of a preparatory phase (opening the fingers) followed
by an executory phase (closing them). If as may be checked at little
cost the preparatory act of opening the grip is completed prior to starting
the transport, then it is clear that the actions of reaching and grasping
will start in succession, in keeping with the principle of proximal precedence.
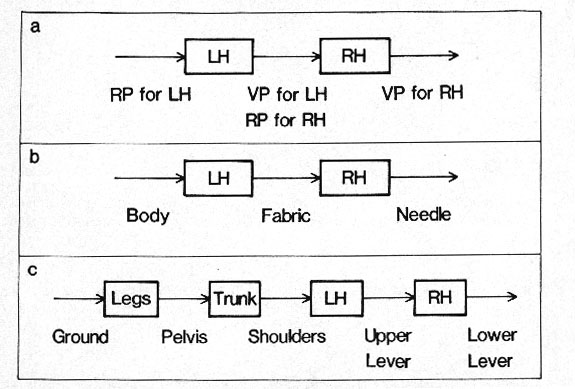
Overview of the model. To sum up what has been said so far, we suggest a comparison of the cooperative action of the left and right hands in the typical differentiated manual gestures of humans to that of a pair of motors occupying contiguous ranks, n and n + 1, respectively, in a serial assembly of motors, or kinematic chain (see Figure 7a). The basic reason that this model is thought to be tenable is that the high-order principles governing the asymmetry of motor bimanual gestures, namely right-to-left spatial reference, macrometric-micrometric contrast and left-hand precedence, have their strict analogues when any pair of contiguous motors in a chain are considered.
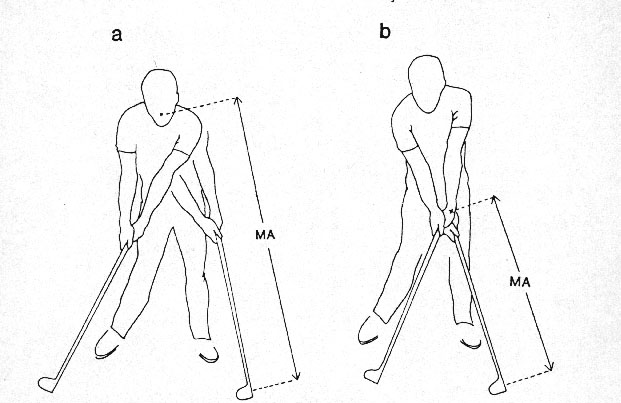
To make the model as unequivocal as possible, three remarks must be made. First, the model says nothing about how many motors must appear in the putative chain: Although many instances of bimanual gestures can be modeled simply enough in terms of a two-motor chain (particularly with seated individuals, see Figure 7b), we should not ignore that manual action often articulates on more proximal action, leading to a model in which the right and left hands occupy the ultimate and penultimate ranks of a chain comprising three or more motors. For example, a golfer's two hands may be represented as motors of ranks 3 and 4, respectively, of a chain whose rank 2 would presumably correspond to rotation of the shoulder line relative to the pelvis, and rank 1 to motion of the pelvis relative to the ground (see Figure 7c).
Second, we need not assume that action of the right hand necessarily ends the chain. Just as we have envisaged that action of the left hand may find its spatial references in action completed at a more proximal level, there is no reason to eliminate the possibility that what the left and right hands do together form the input to another more distal motor organ: The mouth (or the voice) represents the most obvious candidate for occupying a still higher rank in a chain. For example think of musical wind instruments such as a flute, a recorder, or a saxophone: It is noteworthy that the way in which the mouth excites the air column, whose length is controlled by a set of eight or nine fingers, strikingly resembles the way in which the right hand of a violinist excites the string, whose length is controlled by the left hand. There is evidence that the mouth it being understood that we are again globally referring to a complex tract with a number of parts and many functional capabilities is apt to play, when working in close association with one or two hands, the role to which the right hand is normally appointed in bimanual tasks (Guiard, 1987b). First, it happens that the left-right and up-down asymmetry phenomenon described by Ibbotson and Morton (1981; see also Peters, 1985) in a tapping task requiring a regular beat on the part of one limb, and a rhythmic figure on the part of another limb also manifests itself if now the voice and the hand (whether left or right) are involved as effectors. That is, people perform the task markedly better with the voice humming the rhythm and the hand tapping the regular beat than with the converse arrangement. Second, a pianist usually can quite easily sing the right-hand part of a well learnt piece of music, either in unison with or in place of the right hand, while continuing to play with the left hand, whereas attempts to sing the left hand part, whatever its simplicity, while continuing to play the other part with the right hand, lead more often than not to performance blockage. In other words, it appears contrary to nature to accompany one's hand with one's voice in music, just as it is to accompany one's left hand with one's right.
In sum, the suggestion is to liken the cooperative activity of the left and right hands to that of two contiguous motors in a kinematic chain, but this does not mean that the kinematic chain in question must necessarily comprise just two links.
The final comment on the model aims at dissipating a possible ambiguity as regards the two levels of analysis that have been visited so far. It will perhaps seem puzzling to the reader that in its first assumption the kinematic chain model negates the internal complexity of the two manual motors, as each of these two motors is a most typical kinematic chain. In fact, we have analyzed in turn within-limb cooperation and between-limb cooperation, and we have carefully refrained from confounding these two levels. Applied to the description of the behavior of living organisms, the concept of a motor, analogous to that of an effector system (Saltzman & Kelso, 1987), necessarily refers to an abstract entity. What is viewed as a constituent unit at a given level inevitably represents an assembly at a more analytical level. For example, while we may assume that any single degree of freedom at a joint is controlled by a motor, it is clear that this motor is made up of a number of muscles assembled in parallel; a muscle, in turn, may be held to be a motor, but it is known to work thanks to the parallel efforts of fiber groups, and so forth.
The model presented here thus rests on the separate analysis of two
levels of organization. The gist is that organization at the limb level
may serve to model organization at the next higher level corresponding
to the study of human bimanual coordination: Humans, it is suggested, have
developed a general strategy in the use of his two upper limbs such that
from the cooperative action of two arms there emerges, so to speak, a superordinate
arm.
It is appropriate here to briefly examine the question of the possible raison d'être in humans of the principles that appear to govern the relationship between the left and the right manual agents in asymmetrical gestures. The kinematic chain model does suggest a tentative interpretation.
A first suggestion readily arises from the fact that, in a kinematic chain such as an arm, much richness of motion results from the fact that, from level to level, degrees of freedom are added. By analogy, we might say that the remarkable manipulative capabilities of humans, in comparison with those of other primates, have to do with their propensity to imagine and execute actions in which the two hands combine differentiated sub-actions to reach a common end. This view, however, is unsatisfactory. First, not all kinematic chains have the property of adding, in overall action, their internal degrees of freedom: For example, a telescopic arm, regardless of how many components it comprises, can only act on a single dimension. A further problem is that addition of degrees of freedom to the profit of richness of action is not specific to kinematic chains, as an orthogonal assembly of motors presents this property as well. We want, rather, to identify in what general and specific sense it may be advantageous to assemble motors in series.
Perhaps the most important functional characteristic of kinematic chains (characterizing all kinematic chains, and kinematic chains only) is that, as already hinted at in the preceding section, they represent hierarchical structures. We have seen that when two or more motors are assembled in series, there emerges a metric gradient such that the higher the rank of a unit the finer the spatial-temporal resolution of its contribution to global action. I wish to argue that such a division of labor makes it possible, at the level of the whole chain, to overcome the limitations imposed on movement elaboration by Webers law.
If one has at one's disposal a single motor or a set of motors that can only be assembled in parallel for building a machine to do work, one will inevitably have to choose a particular compromise between two mutually exclusive requirements: The machine will produce large amplitude movements if the efforts of its motor are transmitted with a high mechanical advantage, but in this case movements will be relatively coarse; alternatively, the machine will produce finely controlled movements if a low mechanical advantage is adopted, with the drawback, however, that in this case movements will necessarily cover relatively small amplitudes. So with a single motor whether or not it can be construed as consisting of several parallel or orthogonal units at a more analytical level one is imprisoned in the dilemma of Webers law, that is, one must be either far-sighted or near-sighted in action.
The picture will be notably different if one can build the machine by assembling the motors in series. The fundamental difference is that it is now possible to have the machine concurrently work at several levels of resolution and magnitude. For example, consider an anthropomorphic robot arm. It is clear that, thanks to the contribution of its proximal joints, the arm will be able to bring its endpoint to a relatively wide range of positions in the robot's control space (Turvey et al., 1978). But, at the same time, the robot's arm will have the capability of performing very fine resolution movements thanks to the opposite characteristics of its most distal joints. In other words, the movements that can be carried out by a robot's arm or by any other serial assembly of motors can be said to globally violate Webers law, in the sense that the fineness of resolution achieved in moving the arm endpoint can be "abnormally" high, given the wide range of accessible positions, or the range of accessible positions "abnormally" large given the level of resolution that can be achieved.
This reasoning can be extended, beyond mechanical systems, to more abstract domains such as human language and the use of numeral systems. In human languages, the universal feature known as duality of patterning (e.g., Hockett, 1960) amounts to acting hierarchically at a minimum of two levels while producing and receiving a message: One corresponds to forming sentences with words, the other to forming words with speech sounds. With a communication system organized in such a hierarchical fashion, one can elaborate messages that have an extreme accuracy given the virtually infinite repertoire of signal possibilities. Likewise, the fact that one can express, with numbers, any magnitude with as fine a resolution as is desired reflects the hierarchical nature of the numeral systems, which consist of ranked powers of a given base (for example, in the base 10 system, the number 926.14 amounts to 9 X 102 + 2 x 101 + 6 x 100 + 1 x 10-1 + 4 x 10-2): There is no Webers law constraint in the construction of a number, for even when coping with, say, trillions, it remains possible, if perhaps absurd, to be accurate to the thousandth.
To conclude the discussion of human bimanual gestures, it is suggested that the outstanding manipulative efficiency of humans results not only from role differentiation between the two hands but also, and perhaps more significantly, from the fact that between-hand division of labor is typically hierarchical, with the two hands working in a coordinated fashion at two contiguous levels of resolution. Therefore, as a whole, human bimanual skilled gesture can be said to overcome Webers law to the extent that it has the relatively high resolution permitted by the micrometric specialization of the right hand together with the relatively large extension permitted by the macrometric specialization of the left hand. The kinematic chain, a simple application of the hierarchy principle to the realm of movement, may serve, it is hoped, to account with parsimony for this invaluable property of human bimanual actions.
Annett, M. (1967). The binomial distribution of right, mixed and left
handedness. Quarterly Journal of Experimental Psychology, 29, 327-333.
Annett, M. (1970). A classification of hand preference by association analysis. British Journal of Psychology, 61, 303-321.
Annett, M. (1985). Left, right, hand and brain: The right shift theory. Hillsdale, NJ: Erlbaum.
Athenes, S. (1984). Adaptabilite et developpement de la posture manuelle dans l'ecriture: Etude comparative du droitier et du gaucher. Unpublished memorandum. University of Aix-Marseille II.
Belen'kii, J. Ye., Gurfinkel', V. S., & Pal'tsev, Ye. (1967).1. Elements of control of voluntary movements. Biophysics, 12,154-161.
Bernstein, N. (1967). The co-ordination and regulation of movements. Oxford: Pergamon Press.
Beukelaar, L. J., & Kroonenberg, P. M. (1983). Towards a conceptualization of hand preference. British Journal of Psychology, 74, 33-45.
Brain, R. (1941). Visual disorientation with special reference to the lesions of the right cerebral hemisphere. Brain, 64, 244-272.
Briggs, G. G., & Nebes, R. D. (1975). Patterns of hand preference in a student population. Cortex, 11, 230-238.
Broca, P. (1865). Sur le siege de la faculte du langage articule. Bulledn de la Societe d'Anthropologie, 6, 377-393.
Bryden, M. P. (1977). Measuring handedness with questionnaires. Neuropsychologia, 15, 617-624.
Bryden, M. P. (1982). Laterality: Functional asymmetry in the intact brain. New York: Academic Press.
Byron, E. T. (1948). Left-dominant child. Texas State Journal of Medicine, 43, 782-785.
Calvin, W. H. (1982). Did throwing stones shape hominid brain evolution? Ethology and Sociobiology, 3, 115-124.
Cochran, A., & Stobbs, J. (1968). The search for the perfect swing. London: Morrison & Gibb Ltd.
Connelly, l. (1984). Learn the correct role of your hands and arms. Golf World, 23, 6668.
Fitts, P. M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology 47, 381-391.
Flowers, K. (1975). Handedness and controlled movement. British Journal of Psychology, 66, 39-52.
Guiard, Y. (1986). Interlimb role differentiation in pointing with a bimanually held implement. Paper presented at the 27th Annual Meeting of the Psychonomic Society, New Orleans, LA.
Guiard, Y. (1987a). Lateral preferences in right-handers for the bimanual use of long implements. Manuscript in preparation.
Guiard, Y. (1987b). Voice and hand, left and right in music performance: Analogous constraints in division of labour. Manuscript in preparation.
Guiard, Y., & Athenes, S. (1985). Main droite et main gauche dans l'ecriture: La question de la posture "inversee" chez le scripteur gaucher. In Ma/trise du geste et pouvoir de la main chez lienfant, ed. UNICEF, pp. 67-73. Paris: Flammarion.
Guiard, Y., & Millerat, F. (1984). Writing postures in left-handers: Inverters are hand crossers. Neuropsychologia, 22, 535-538.
Hampson, E., & Kimura, D. (1984). Hand movement asymmetry during verbal and non
verbal tasks. Canadian Journal of Psychology, 38, 102-125.
Hecaen, H., & de Ajuriaguerra, J. (1964). Left handedness: Manual superiority and cerebral dominance. New York: Grune and Stratton.
Hockett, C. F. (1960). The origin of speech. Scientific American, 203, 88-106.
Hollerbach, J. (1980). Understanding manipulator control by synthesizing human handwriting. In P. H. Winston & R. H. Brown (Eds.), Artificialintelligence, an MlT perspective (pp. 312-332). Cambridge, MA: MIT Press.
Ibbotson, N. R., & Morton, J. (1981). Rhythm and dominance. Cognition, 9, 125-138.
Jeannerod, M. (1981). Intersegmental coordination during reaching at natural visual objects. In J. Long & A. Baddeley (Eds.). Attention and Performance IX (pp. 153-168). Hillsdale, NJ: Erlbaum.
Keiso, J. A. S., Southard, D. L., & Goodmap, D. (1979). On the coordination of twohanded movements. Journal of Experimental Psychology: Human Perception and Performance, 5, 229-238.
Kimura, D. (1961). Cerebral dominance and the perception of verbal stimuli. Canadian
JouMal of Psychology, 15, 166-171.
Kimura, D. (1973). Manual activity during speaking. l. Right-handers. Neuropsychologia, 11, 45-50.
Kimura, D. (1982). Left-hemisphere control of oral and brachial movements and their relation to communiication. Philosophical Transactions of the Royal Society of London, B298, 135-149.
Kimura, D., & Archibald, Y. (1974). Motor function of the left hemisphere. Brain, 97, 337350.
Kimura, D., & Humphrys, C. A. (1981). A comparison of left- and right- arm movements during speaking. Neuropsychologia, 19, 807-812.
Kugler, P. N., Kelso, J. A. S., & Tumey, M. T. (1980). On the concept of coordinative structures as dissipative structures: I. Theoretical lines. In G. E. Stelmach & J. Requin (Eds.), Tutorials in motor behavior (pp.3-47). Amsterdam: North-Holland Publishing Company.
Lepine, D., & Requin, J. (1983). Specification of spatial dimensions in movement programming. Society for Neuroscience Abstracts, 9, 297-17.
MacNeilage, P. F., Studdert-Kennedy, M. G., & Lindblom, B. (1984). Functional precursors to language and its lateralization. American JouMal of Physiology (Regulatory, Integrative and Comparative Physiology), 15, R912-R914.
Meyer, D. E., Smith, J. E. K., & Wright, C. E. (1982). Models for the speed and accuracy of aimed movements. Psychological Review, 89, 449- 482.
Navon, D. (1977). Forest before trees: The precedence of global features in visual perception. Cognitive Psycho/ogy, 9, 353-383.
Nebes, R. D. (1971). Superiority of the minor hemisphere in commissurotomized man for the perception of part-whole relations. Cortex, 7, 333-349.
Newcombe, F. (1969). Missile wounds of the brain. Oxford: Oxford University Press.
Nicklaus, J. (1983). Five views of my new swing. Golf World, 22, 42-43.
Oldfield, R. C. (1969). Handedness in musicians. British Journal of Psychology, 60, 9199.
Oldfield, R. C. (1971). The assessment and analysis of handedness: The Edinburgh inventory. Neuropsychologia, 9, 97-113.
Paillard, J., & Beaubaton, D. (1978). De la coordination visuo-motrice a ['organisation de la saisie manuelle. In H. Hecaen & M. Jeannerod (Eds.), Du contro/e de /a motricite a ['organisation du geste (pp. 225- 260). Paris: Masson.
Peters, M. (1980). Why the preferred hand taps more quickly. Canadian JouMal of Psychology, 34, 62-71.
Peters, M. (1981). Attention asymmetries during concurrent bimanual performance. The Quarter/y Journal of Experimental Psychology, 33A, 95- 103.
Peters, M. (1983). Differentiation and lateral specialization in motor development. In G. Young, S. J. Segalowitz, C. M. Carter, & S. E. Trehub (Eds.), Manual specialization and the developing brain (pp. 141- 159). New York: Academic Press.
Peters, M. (1985). Constraints in the performance of bimanual tasks and their expression in unskilled and skilled subjects. The Quarter/y Journal of Experimental Psychology, 37A, 171-196.
Porac, C., & Coren, S. (1981). Lateral preference and human behavior. New York: Springer Verlag.
Provins, K. A., Milner, A. D., & Kerr, P (1982). Asymmetry of manual preference and performance. Perceptual and motor skills, 54, 179194.
Riehle, A., & Requin, J. (1985). Neuronal activity changes related to the advance information about biomechanical parameters of an intended movement. Society for Neuroscience Abstracts, 11, 705.
Saltman, E., & Kelso, J. A. S. (1987). Skilled actions: A task-dynamic approach. Psychological Review, 94, 84-106.
Satz, P (1979). A test of some models of hemispheric speech organization in the leftand right-handed. Science, 203, 1131 -1133.
Schmidt, R. A., Zelaznik, H., Hawkins, B., Frank, J. S., & Quinn, J. T., Jr. (1979). Motor output variability: A theory for the accuracy of rapid motor acts. Psychological Review, 86, 415-451.
Schonen, S. de (1977). Functional asymmetries in the development of bimanual coordination in human infants. JouMal of Human Movement Studies, 3, 144-156.
Stevens, L. T. (1886). On the time sense. Mind (GB), 11, 393-404.
Todor, J. A., & Kyprie, P. M. (1980). Hand difference in the rate and variability of rapid tapping. Journal of Motor Behavior, 12, 57-62.
Turvey, M. T., Rosenblum, L. D., Kugler, P. N., & Schmidt, R. C. (1986). Fluctuations and phase symmetry in coordinated rhythmic movements. JouMal of Experimental Psychology: Human Perception and Performance, 12, 564-583.
Turvey, M. T., Shaw, R. E., & Mace, W. (1978). Issues in the theory of action: Degrees of freedom, coordinative structures and coalitions. In J. Requin (Ed.), Attention and performance Vll (pp. 557-594). Hillsdale, NJ: Erlbaum.
Tzeng, O. J. L., & Wang, W. S. Y. (1984). Search for a common neurocognitive mechanism for language and movements. American Jouma/ of Physiology (Regulatory, Integrative, and Comparative Physiology), 15, R904-R911.
Wing, A. (1978). Response timing in handwriting. In. G. E. Stelmach (Ed.), Information processing in motor control and learning (pp. 153- 171). New York: Academic Press.
Wing, A. (1982). Timing and co-ordination of repetitive bimanual movements. Quarter/y Journal of Experimental Psychology, 34A, 339-348.
Wing, A. (1986). Paper presented at the Annual Meeting of the European Neurosciences Association, Marseille, France.
Woodworth, R. S. (1899). The accuracy of voluntary movement. Psychological
Review, 3, 1-114.
Submitted February 2, 1987. Revision submitted July 1, 1987.