Abstract

I present an example of human learning that falls outside linguistic schema theories, illustrating representation creation as perceptual interaction at both interpersonal and gestural-material levels. I focus on sequences of activity in which students' interpretation of what constitutes a representational language (and what it means) changes as they construct models of what they are seeing and doing. This social-perceptual analysis complements linguistic schema theories of novice-expert differences with more detailed learning mechanisms, emphasizing especially the nature of perception. This perspective leads to new experimentation and ways of observing and understanding student interaction with today's instructional programs.

1. Towards a social-perceptual account of learning

There are two limitations to this approach: First, it tends to ignore the process by which students learn a representational notation, since it is taken for granted that the significant forms on the screen are self-evident; learning to perceive these forms lies outside the theory of knowledge representation. Second, the transfer paradigm doesn't teach students how to create their own representational notations and languages; learning is construed as learning someone else's ("standard") notation and theories.

In effect, the development of instructional programs would benefit from a more careful consideration of how representations are created and given meaning in a shared perceptual space, out where they are spoken, written, and drawn. Interactions between people every split second--a blush, a gesture, an intonation--are causing us to perceive different things, to speak and view the world differently. This external environment includes the interpersonal level (e.g., the dynamics between a teacher and group of students vying for attention) and the gestural-material level (e.g., the representational medium, such as drawings, and perceivable, attention-getting gestures in this medium, such as pointing or saying where to look) (Roschelle and Clancey, 1992).

Put simply, a learner participates in the creation of what is to be represented and what constitutes a representation. This dialectic process can be modeled by schema transformations of assimilation, refinement, etc. (e.g., Norman, 1982), in which linguistic structures are logically combined in an individual mind. But such a mechanism posits a set of descriptive primitives in the mind out of which all expressions are formed, and therefore fails to account for the process by which new representational languages are created. A mechanism grounded in linguistic schemas also fails to account for individual differences, because it assumes that there is one objective world of features that everyone can perceive. A linguistic schema mechanism especially fails to acknowledge or explain what is problematic to the learner, namely determining what needs to be understood (Lave, 1988).

1.1 Representational flatland

I F    the site of the culture is normally sterile and
        the gram-stain of the organism is negative,
THEN there is strongly suggestive evidence that there is significant disease associated with this occurrence of the organism.

In the work of Jeanne Bamberger (1991), which has influenced my analysis a great deal, children represent musical tunes with Montessori Bells (unlabeled metal bells playing different musical notes) or sticks of wood of different colors and sizes. The position of a bell or of a block can represent what a child hears, but the description of the bell or block is not equivalent to its meaning. For example, a given bell-tone (such as "middle C") appearing at different places in a tune is not labeled in the same way by a child, because it sounds differently, depending on where it appears in the tune.

Similar analysis of speech perception reported by Rosenfield (1988) suggests that "sounds are categorized and therefore perceived differently depending on the presence or absence of other sounds." For example, there is "a trade-off between the length of the sh sound and the duration of the silence [between the words of "say shop"] in determining whether sh or ch is heard....Lengthening the silence between words can also alter the preceding word" (Rosenfield, 1988, p. 107). For example, "if the cue for the sh in ëship' is relatively long, increases in the duration of silence between the words ["gray ship"] cause the perception to change, not to ëgray chip' but to ëgreat ship.'" Hence, phonemes are not given but constructed within an ongoing context of overlapping cues. "What brain mechanism is responsible for our perceptions of an /a/, if what we perceive also depends on what came before and after the /a/?" (p. 110) The basic claim is that "the categorizations created by our brains are abstract and cannot be accounted for as combinations of ëelementary stimuli.'" There are no innate or learned primitives like /a/ to be found in the brain; that is, there are no primitive stimuli descriptions in the brain that can be combined. There are just patterns of brain activity that correspond to organizations of stimuli (Freeman, 1991). Our perception depends on past categorizations, not on some absolute, inherent features of stimuli (such as the frequencies of sounds) that are matched against inputs (Rosenfield, 1988, p. 112).

1.2 The origin of descriptions

Most cognitive theories of learning claim that linguistic descriptions come from other linguistic descriptions, by a process of refinement, generalization, and composition. Data to be represented is expressed as programmer-supplied primitive categories and measurable features. Linguistic schema models assume that the world comes pre-represented, already parameterized into objects and features. Since the world can be described as objective fact, this is viewed as just bootstrapping the program. Researchers may ask, "What is the raw material of reasoning?" (Koedinger and Anderson, 1990), but they tend to give one choice: varieties of descriptions. Even models of learning that involve "recalling specific instances," that is, going back to experiences, deal only with descriptions of experience.

Where do descriptions come from? Some researchers (e.g., Bickhard and Richie(1983); Edelman (1992)) claim that a non-linguistic neural process is required, coordinating perception and conceptualization that makes language possible. But in the exclusively linguistic cognitive model, rules like those in Guidon rest on nothing but more words--definitions, causal relationships, classifications. Surprisingly, though it is well-known that such models are "ungrounded," that the symbols have no meaning to the program itself, little attempt has been made to find out how people create symbolic forms. What are the non-linguistic processes that control attention, affect reconceptualization, and correlate disparate ways of seeing? How does interpersonal activity bias and redirect these internal processes?

I wish to emphasize that integrating social and perceptual perspectives also involves explaining what is right about schema-based (linguistic) models. Descriptions of novice-expert differences, reasoning strategies, explanation-based learning, etc. provide clues about the effect of practice, that is, how experience biases future behavior. A social-perceptual model will complement these descriptions with more detailed learning mechanisms, emphasizing especially the nature of perception. Perhaps most significantly, this perspective leads to new experimentation and ways of observing and understanding student interaction with today's instructional programs.

In this paper, I present an example of human learning that falls outside linguistic schema theories, illustrating representation creation as perceptual interaction at both interpersonal and gestural-material levels. We shift from talking about theories stored in the head to a fresh study of the forms people create and perceive. We focus especially on sequences of activity in which students' interpretation of what constitutes a representational language (and what it means) changes as they construct models. What is problematical to students as they attempt to discover meaningful forms on the computer screen? As observers, we must figure out what the students are seeing, for they aren't necessarily the forms the instructional designer intends. In conclusion, I outline research areas emerging from the intersection of social, neuropsychological, and cognitive psychology perspectives.

2. Example: Green Globs

The students appear to be asking: What am I seeing? What forms am I supposed to be seeing? Is this form intended to be a representation? How do I correlate verbal descriptions on the worksheet with what I am seeing? What does this word mean, given what I am seeing? Can I apply this term to both examples? Where are the examples I am supposed to describe by this term? The students are attempting to correlate personal interpretations with given terminology, instructions, and another person's representational claims and actions. What biases are caused by interpersonal interactions? How does working together facilitate or inhibit alternative ways of seeing? How are alternative categorizations reconciled?

The following worksheet excerpt was produced by Paula and Susanna. Helvetica font indicates worksheet text. Los Angeles font indicates student writing, with Paula's writing in boldface (she uses an x to dot the letter "i"; Susanna uses an open dot). Comments are in Times italics.

------------------------------------------------------------------

{To this point, Paula and Susanna have been introduced to the idea of the graph of an equation. They have plotted points that satisfy linear equations and observed that they fall on a line. They will now use the computer for plotting lines.}

All at Once

Point plotting is one way to graph equations, but it is fairly time-consuming. The following activities will help you learn how to graph equations without plotting points. We will be using a computer program that can graph equations for you.

Choose 4 for Equation Plotter from the index. Then choose 2 for Rectangular grid for the next menu. Press return once more.

Type in the equation Y = 2X + 1. Hit return and see what happens.

Now type in the equation Y = -5/3X + 6.7. Hit return and see what happens.

As you may have noticed, the graphs of both of these equations are straight lines. As you will discover, any equation of the form Y = [2]X + [2] (with numbers in place of the boxes)   will produce a straight line when you graph it. Try choosing some different numbers to put in the boxes, and see what their graphs look like.

{The students have written the number 2 in both boxes.}

We're going to try to make some sense out of why different numbers produce different lines. First, let's see what you can figure out on your own. Try typing in some equations, and see if you can predict what their lines will look like. Please keep track of which equations you try and what you find out.
 

Positive numbers

Y = 2X + 1

Y = 3X + 1

Y = 4X + 1

What do you notice? The lines are not very straight.
How are these lines similar? They are
How are they different? Each one is thicker than the other one.
What do you think will happen if you type in Y = 5X +1? That the equation is not going
Sketch your prediction on this empty graph and then try it on the computer. to get thicker
                                                                                  &nb sp;                                                           straight.

{"not" is inserted before "going" and "thicker" is smudged out above "straight "}

------------------------------------------------------------------

3. Discussion

What is happening here? First, the students were never told what features to look for in the graphed lines, simply to compare them. The text opens by using the word "straight" twice: "these equations are straight lines... will produce a straight line..." So what is a non-straight line? Told to graph many examples and compare them, the students need a basis of comparison. Straightness has been suggested as a property of some equations. Perhaps the students can discover equations producing lines that aren't straight?

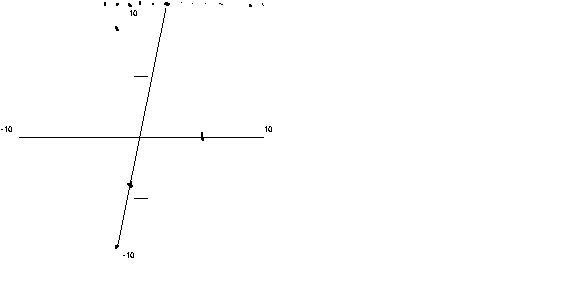
Indeed, the students find that some lines are straighter and some are thicker. Here is an important clue--the students are looking at the pixels on the screen (Figure 1). Nearly vertical lines, such as Y = 5X +1 shown here are "not really straight" because the pixel grid is too coarse--the line appears jagged. (For example, in Figure 1, the near-vertical line is represented as adjacent segments of line segments three pixels in length.)
 

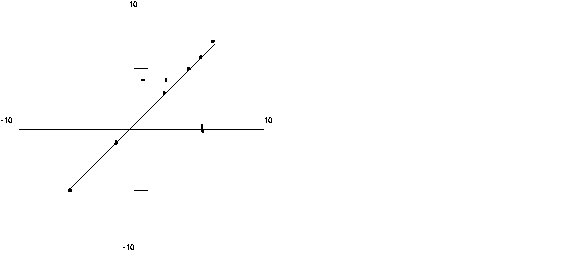
The equation Y = 1X + 1 is straight for at least two reasons: the grid dots are perfectly connected and the pixel representation is less jagged. However, as we move to the horizontal (Y = 1/2X + 1), the lines become jagged again. As the slope decreases (Y = 1/5X + 1), the line is becoming more nearly horizontal and so apparently more "straight."

This unfortunate interaction is sobering for designers of computer interfaces and instructional text. Clearly, more guidance about what to look for on the screen would have been possible and might have helped. But in practice it is impossible to anticipate all the alternative ways of seeing the screen. Understanding what "straight" means is not a matter of memorizing a definition, but of coordinating (and creating) possible meanings of the words with what you are seeing. For example, suppose we told Paula and Susanna that "straight means that the dots you plotted are lined up." What does "lined up" mean? Do "the dots you plotted" include the intermediate dots the computer filled in for you, that is, the pixels you caused to appear on the screen? Without even this guidance, Paula and Susanna brought in alternative interpretations from their experience: straight up (perhaps like a rocket) and flat (perhaps like a desert).
 
This example illustrates how people come to view forms as being representations. How would we simulate Paula and Susanna's behavior using linguistic schema models? If we start by entering as input the equations of the lines (e.g., (SLOPE LINE-1 45 degrees)) we will build in as primitive meaningful forms the notation that Paula and Susanna are trying to understand. On the other hand, neither student talks about the pixels on the screen; they might not make a conceptual distinction between the visible dots and how the display works. So what is to be the input to the simulation program? We must conclude that the input is the entire screen and changes to its forms over time, including where the students are pointing. But such a cognitive model would have to begin with perceptual processes and not notations stored in memory in some language. Indeed, if models of language learning leave out processes by which gestures are used to disambiguate meaning, then what aspects of language and conversation have we attempted to understand in our cognitive models? 

Again, the "situated" aspect of cognition is that the world is not given as objective forms; rather, what we perceive as properties and events is constructed in the context of coordinated activity. Representational forms are constructed and given meaning in a perceptual process, which involves interacting with the environment, detecting differences and similarities, and hence creating information (Reeke and Edelman, 1988; Maturana, 1983). As a perceived form, marks on the screen have no inherent meaning, but are instead viewed as symbolic in the context of how they display mathematical relations--which the students are attempting to learn. Crucially, the internal processes controlling perception, biasing categorizing and directing attention to particular details, are themselves organized by the ongoing interactions, that is, the perceptions and movements the person is already coordinating at this time (Rosenfield, 1988). Paula's interpretation of Susanna's explanations are biased by what she sees on the screen, including the relative thickness of the lines and Paula's gestures. The result is a collaborative construction: The worksheet doesn't simply "transfer" the meaning of "line" to the two children and they don't transfer it to each other. Indeed, they are engaged in a creative negotiation of what a straight line could be.

To draw educational computing implications more clearly, notice that all the students have to work with are the instructional designer's representations--the worksheet and what appears on the computer screen. The students are attempting to coordinate what they see with their interpretations and strategies for making sense during a classroom exercise. It is not especially profound to point out that the instructional designer must make his meanings clear and try to direct the student's attention appropriately. However, definitions and procedures are always open to interpretation. The trick is to embed this interpretation process within an activity (such as manipulating things on the screen), so the feedback of the activity biases the student's attention and, hence, sense of what is significant.

In particular, the Green Globs activity could relate the concept of slope to the properties of everyday surfaces. For example, a game could be devised by which a very slow-moving ball is kept in some preferred area near the center of the screen by drawing lines that it bounces off. The line would be like a paddle. The students would need to quickly communicate to each other what kind of line should be drawn next ("more vertical," "something at an angle"), as they realize that lines perpendicular to the ball's current path are preferred.

The example of relating the word "straight" to sensation, what is felt or seen, illustrates some of the aspects by which representations are created and given meaning:

1)    The meaning of many concepts is grounded in direct physical experience: including images, feelings, sounds, and posture (Lakoff, 1987). Understanding words like "straight" involves a perceptual process of categorizing. Understanding the meaning of a word cannot be reduced to memorizing a definition because the terms in the definition would be ungrounded in experience (as exemplified in the students' struggle with "straight").

2)    Relating concepts involves returning to (reperceiving) sensory experiences (Bartlett, 1932; Schön, 1979; Bamberger and Schön, 1983), sensing new details, and forming new categories that correlate different experiences associated with the originally disparate concepts. Apparently the same process that leads us to look again or listen again to actual physical materials is at work as we relate concepts in our head, recalling associated details (often images) (Bartlett, 1932).

3)    Learning new concepts generally involves a process of interacting with physical materials in a social setting (Lave, 1988). Different ways of structuring materials are tried out as different ways of talking direct each individual's attention to different ways of seeing.

In related work, (Roschelle and Clancey, 1993) consider further the process of constructing new physics concepts in conversations, focusing especially on how previous conceptions (metaphors) direct attention and how perceived forms come to be viewed as representations.

4. Conclusion: Triangulating Social, Neural, and Representational Perspectives

To explain how human conceptualization and behavior routines described by representational psychology are possible, we must take into account the interactions that occur between internal perceptual and external social processes. My analysis pivots around one fundamental idea: Human memory is not a place where linguistic descriptions are stored (in the manner of a computer memory). A corollary is that descriptions are created, given meaning, and influence behavior by interactions of internal and external processes. Specifically, we study how interpersonal and gestural-material processes (figural schemas) change attention, what is perceived, and what is represented (formal schemas).

Connecting the three perspectives of Figure 2 are new aspects of a theory of cognition. We shift from the "individualist" point of view of linguistic schema models, which take what goes on inside the head of a person to be the locus of control. We seek to explain the observed patterns of human behavior in terms of interactions between people and between internal and external processes. Research questions shift to studying how structures are created and maintained at three distinct levels: social organizations, physical materials, and internal perceptual processes. How is patterning possible? What interaction of structure changes in the brain, organizations of physical materials, and guidance by people in the community change and conserve behavior routines?

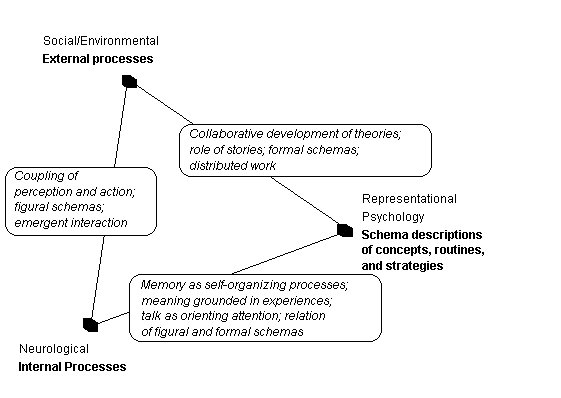
Figure 2. New perspectives relating internal and external processes to descriptions of knowledge and behavior.

Instructional design based on the constructive nature of learning, already well-established in some circles (Papert, 1990), could take into account interpersonal and gestural-material aspects of perception. Instructional designers might correlate their static view of subject material (e.g., the concept of a linear equation, the concepts of acceleration and velocity) with what is on the computer screen and the activities of the students. They must project how activity will bias perception, and hence structure the student's categorizing. Ideas like "reflection" and "multiple representations" have been around for some time (Schön, 1987). Situated cognition provides a new way of integrating good instructional ideas, a new way of thinking about cognitive science theories, and a new way of looking at the data.

In equating human knowledge with descriptions (e.g., expert system rules), we eliminated the grounds of belief, and greatly oversimplified the complex processes of coordinating perception and action; we objectified what is inherently an interactive, subjective process. We must be careful where we draw lines in our experience: between people, between people and materials, between materials and the brain. Interactions are occurring throughout; it is a mistake to attribute the patterns to the society, to the physical world, to the brain, or even to the observer-theoretician.

Perhaps the greatest benefit of situated cognition is providing grounds for researchers and practitioners to work together. Ethnographers, computer scientists, subject matter experts, teachers, and students need each others' point of view to integrate theory, practice, and instructional design (Schön, 1987). This collaboration grounds theoretical issues about memory, information, and perception in the design of computer tools. What are the properties of computer activities that engage students in conversations about what they know and facilitate multiple ways of seeing and talking? By asking such questions, we can consolidate arguments about coaching, discovery, and tutoring, and better focus our efforts to use computers appropriately.

References

Bamberger, J. and Schön, D.A. 1983. Learning as reflective conversation with materials: Notes from work in progress. Art Education, March.

Bartlett, F. C. [1932] 1977. Remembering­-A Study in Experimental and Social Psychology. Cambridge: Cambridge University Press. Reprint.

Bateson, G.1988. Mind and Nature: A necessary unity. New York: Bantam.

Bickhard, M. H. and Richie, D.M. 1983. On the Nature of Representation: A Case Study of James Gibson's Theory of Perception. New York: Praeger Publishers.

Bransford, J.D., McCarrell, N.S., Franks, J.J., and Nitsch, K.E. 1977. Toward unexplaining memory. In R.E. Shaw and J.D. Bransford (editors), Perceiving, Acting, and Knowing: Toward an Ecological Psychology. Hillsdale, New Jersey: Lawrence Erlbaum Associates, pps. 431-466.

Chi, M.T.H., Glaser, R., and M.J. Farr (editors) 1988. The Nature of Expertise. Hillsdale: Lawrence Erlbaum Associates.

Clancey, W. J. 1987. Knowledge-Based Tutoring: The GUIDON Program. Cambridge, MIT Press.

Edelman, G.M. 1992. Bright Air, Brilliant Fire: On the Matter of the Mind. New York: Basic Books.

Freeman, W. J. 1991. The Physiology of Perception. Scientific American, (February), 78-85.

Gardner, H. 1985. The Mind's New Science: A History of the Cognitive Revolution. New York: Basic Books.

Gibson, J. J. 1966. The Senses Considered as Perceptual Systems. Boston: Houghton Mifflin Company.

Gregory, B. 1988. Inventing Reality: Physics as Language . New York: John Wiley & Sons, Inc.

Iran-Nejad, A. 1987. The schema: A long-term memory structure or a transient functional pattern. In R. J. Tierney, Anders, P.L., and J.N. Mitchell (editors), Understanding Readers' Understanding: Theory and Practice, (Hillsdale, Lawrence Erlbaum Associates)

Jenkins, J.J. 1974. Remember that old theory of memory? Well, forget it! American Psychologist, November, pps. 785-795.

Koedinger, K. R., & Anderson, J. R. 1990. Abstract planning and perceptual chunks: Elements of expertise in geometry. Cognitive Science, 114(4), 511-550.

Lakoff, G. 1987. Women, Fire, and Dangerous Things: What Categories Reveal about the Mind. Chicago: University of Chicago Press.

Langer, S. K. 1942. Philosophy in a New Key: A Study in the Symbolism of Reason, Rite, and Art. New York: The New American Library.

Larkin, J. H., & Simon, H. A. 1987. Why a diagram is (sometimes) worth ten thousand words. Cognitive Science, 11(1), 65-100.

Lave, J. 1988. Cognition in Practice. Cambridge: Cambridge University Press.

Maturana, H. R. 1983. What is it to see? ¿Qué es ver? 16:255-269. Printed in Chile.

Neisser, U. 1976. Cognition and Reality: Principles and Implications of Cognitive Psychology. New York: W.H. Freeman.

Newell, A. 1990. Unified Theories of Cognition.

Norman, D.A. 1982. Learning and Memory. New York: W.H. Freeman and Company.

Papert, S., 1990, Introduction to Constructionist Learning. In I. Harel (editor), A 5th Anniversary Collection of Papers Reflecting Research Reports, Projects in Progress, and Essays by the Epistemology & Learning Group, The Media Laboratory, MIT, Cambridge, Massachusetts.

Reeke, G.N. and Edelman, G.M. 1988. Real brains and artificial intelligence. Daedalus, 117 (1) Winter, "Artificial Intelligence" issue

Roschelle, J. 1991. The computer as a medium for conversations. In preparation.

Rosenschein, S.J. 1985. Formal theories of knowledge in AI and robotics. SRI Technical Note 362.

Rosenfield, I. 1988. The Invention of Memory: A New View of the Brain New York: Basic Books.

Schank, R. C., & Abelson, R. 1977. Scripts, Plans, Goals and Understanding. Hillsdale, New Jersey: Lawrence Erlbaum Associates.

Schön, D.A. 1979. Generative metaphor: A perspective on problem-setting in social policy. In A. Ortony (Ed), Metaphor and Thought. Cambridge: Cambridge University Press. 254-283.

Schön, D.A. 1987. Educating the Reflective Practitioner. San Francisco: Jossey-Bass Publishers.

Simon, H. A. 1969. The Sciences of the Artificial. Cambridge, MA: MIT Press.

Suchman, L.A. 1987. Plans and Situated Actions: The Problem of Human-Machine Communication. Cambridge: Cambridge Press.

Tyler, S. 1978. The Said and the Unsaid: Mind, Meaning, and Culture. New York: Academic Press.

Winograd, T. and Flores, F. 1986. Understanding Computers and Cognition: A New Foundation for Design. Norwood: Ablex.