Chapter 2
AN INTRODUCTION TO QUANTITATIVE GENETICS
Wim E. Crusio
Génétique, Neurogénétique et Comportement
UPR 9074 CNRS, Institut de Transgénose
3b, rue de la Férollerie
45071 Orléans Cedex 02, France
Send correspondence and proofs to Dr. Wim E. Crusio at the above
address.
Tel: (33) 2 38 25 79 74; Fax: (33) 2 38 25 79 79
E-mail: crusio@cnrs-orleans.fr
It is kindly requested that no changes or "corrections" be made in
the manuscript without prior consent of the author. Thank you.
Summary
This chapter provides a brief overview of quantitative-genetic theory.
Quantitative-genetics provides important tools to help elucidate the genetic
underpinnings of behavioral and neural phenotypes. This information can
then provide substantial insights into the previous evolutionary history
of a phenotype, as well as into brain-behavior relationships.
The most often employed crossbreeding designs are the classical Mendelian
cross and the diallel cross. The information rendered by the former is
limited to the two parental strains used and cannot be broadly generalized.
The principal usefulness of this design is for testing whether a given
phenotype is influenced by either one gene or by more genes. The diallel
cross renders more generalizable information, the more so if many different
strains are used, such as estimates of genetic correlations. To estimate
the latter, correlations between inbred strain means may provide a helpful
shortcut.
Some commonly encountered mistakes in the interpretation of the results
of quantitative-genetic studies are presented and explained.
1. Introduction
Behavior is an animal's way of interacting with its environment and is
therefore a prime target for natural selection. Furthermore, as behavior
is the output of an animal's nervous system, this indirectly leads to selection
pressures on neuronal structures. In consequence, each species' behavior
and nervous system have co-evolved in the context of its natural habitat
and can be properly comprehended only when their interrelationships are
regarded against that background [4]. To arrive at a profound understanding
of neurobehavioral traits, one will therefore have to consider problems
of causation. Van Abeelen [37] distinguished between the phenogenetic and
the phylogenetic aspects of causation. Both aspects deal with the genetic
correlates of neurobehavioral traits, the first in a gene-physiological,
the second in an evolutionary sense. In other words, neurobehavioral geneticists
try to uncover the physiological pathways underlying the expression of
a trait and to evaluate its adaptive value for the organism. As I have
shown before [9], quantitative-genetic methods may be employed with profit
to address problems related to both aspects of causation.
2. Phylogenetic Aspects of Causation
2.1. NATURAL SELECTION AND GENETIC ARCHITECTURE
Selection pressures mold a population's genetic make-up, which subsequently
will show traces of this past selection. Therefore, information about the
genetic architecture of neurobehavioral traits might permit us to deduce
the probable evolutionary history of these traits [2]. With genetic architecture
we mean all information pertaining to the effects of genes influencing
a particular phenotype in a given population at a given time, including
information concerning the presence and size of certain genetic effects,
the number of genetic units involved, etc. Generally, however, information
about the presence and nature of dominance suffices [7].
With very few exceptions, natural, non-pathological variation in neurobehavioral
phenotypes is polygenically regulated. If dominance is present, we may
envisage two different situations: either (uni)directional or ambidirectional
dominance. In the first case, dominance acts in the same direction for
all genes involved (e.g., for high expression of the trait), whereas in
the latter case it acts in one direction for some genes and in the opposite
one for others. In its most extreme form, ambidirectional dominance may
lead to situations where an F1 hybrid is exactly intermediate between its
parents, despite the presence of strong dominance effects.
Mather [29] distinguished between three kinds of selection: stabilizing,
directional, and disruptive. Stabilizing selection favors intermediate
expression of the phenotype, directional selection favors either high or
low expression, whereas with disruptive selection more than one phenotypic
optimum exists. Disruptive selection will lead to di- or polymorphisms,
which may be in stable equilibrium or may even lead to breeding isolation
and incipient speciation [35]. The commonest example of a dimorphism is
the existence of two sexes, whereas a possible example of speciation as
a consequence of disruptive selection is the explosive adaptive radiation
and speciation found among fish species belonging to the family Cichlidae
in the great East-African lakes [20].
Selection acts in favor of those genotypes that not only produce the
phenotype selected for, but are also capable of producing progeny that
differs little from this phenotype. In the end, this results in a population
whose mean practically coincides with the optimum. Stabilizing and directional
selection have therefore predictably different consequences for the genetic
architecture of a trait. Genes for which a dominant allele produces a phenotypic
expression opposite to the favored direction will become fixed very rapidly
for the recessive allele under directional selection. A similar rapid fixation
will then occur for genes for which dominance is absent, i.e., where the
heterozygote is intermediate between the two homozygotes. In contrast,
selection against recessive alleles is much slower. The result will be
that after only a relatively short period of directional selection the
first two types of genes will not contribute to the genetic variation within
the population anymore. Those genes where the dominant allele produces
the favored phenotypical expression will remain genetically polymorphic
for a much longer time, conserving genetic variance. Thus, directional
selection leads to situations where dominance is directional, in the same
direction as the selection. Stabilizing selection leads to situations where
dominance is either absent or ambidirectional. Furthermore, directional
selection generally results in lower levels of genetic variation than ambidirectional
selection does [29]. The genetic architecture of a trait may be uncovered
by using appropriate quantitative genetic methods.
2.2. Theoretical Background
At this point, a brief excursion into the field of quantitative genetics
is necessary. For the sake of simplicity, considerations of possible interactions
between genes (epistatic interactions) will be omitted from the present
treatment. Similarly, we will assume that sex-linked genes as well as pre-and
postnatal effects are absent. Pertinent references and more technical details
for cases where these simplifying assumptions do not hold true may be found
in [7].
Classical Mendelian analysis studies characters influenced by a limited
number of genes, two or three at the most, that are easy to separate into
discrete phenotypic classes. Many characters, however, show continuous
gradations of expression and are not separable into discrete classes (so-called
quantitative traits). The simultaneous actions of a large number of genes
(polygenes), combined with phenotypic deviations caused by variations in
the environment (environmental variance, E), may explain such patterns
of phenotypic variation [19]. The genetic contribution to a phenotype can
then be divided into two main sources: additive-genetic effects and dominance
deviations. In the case of one single gene, with alleles A and a, we may
denote the phenotypical values of the three possible genotypes as follows:
AA = m + da
Aa = m + ha
aa = m - da
(1)
The parameter da is used to represent half the difference
between the homozygotes, ha designates the deviation
of the heterozygote from the midparental point m. Note that in quantitative
genetics capital letters are used to indicate increaser alleles, which
are not necessarily also the dominant ones. Hence, da is
positive by definition, whereas ha may attain all possible
values. If we now consider two inbred strains A and B in a situation where
many genes affect the phenotype, we may denote the average phenotype of
strain A by
m + S(d+) + S(d-)
(2)
(shortened to m + [d] for ease of representation), where S(d+)
indicates the summed effects of those genes that are represented by their
increaser alleles and S(d-) indicates the same for decreaser
alleles. Parameter m is a constant, reflecting the average environmental
effects both strains have in common as well as genetic effects at loci
where the strains are fixed for the same alleles. The average phenotype
of strain B will then equal m - [d]. Similarly, the phenotypic value
of an F1 hybrid between A and B may be written as
m + S(h+) + S(h-)
(3)
(shortened to m + [h]). It must be noted that [h] is the
sum of the dominance deviations of many genes. If these effects are balanced
in opposite directions, [h] can be low or zero, even with dominance
present. The same applies to [d], of course.
Because variations in a phenotype can be thought of as the summed effects
of variations in genotype and environment, plus the interaction and covariation
between these two factors, we may express the phenotypic variance P
of a population as:
P = G + E + G*E + 2cov(g,e)
(4)
In the controlled situation of animal experiments in the laboratory (but
not in the field) the covariance between genotype (g) and environment
(e) can be minimized. Further, the absence of genotype-environment
interaction means that all individuals, regardless of phenotype, will have
similar sensitivities to environmental variations. As a result, genetically
homogeneous groups (for example, inbred strains and their F1
hybrids) should exhibit similar variances. If such is not the case, the
effects of (G*E) may often be removed by choosing an appropriate
measurement scale [6], leaving
P = G + E
(5)
The genetic component of the variance (G) can, of course, be divided
into components due to additive-genetic variation (D) and dominance
deviations (H).
We may demonstrate the partitioning of genetic variance into its additive-genetic
and dominance components by the example of an F2 cross between
two inbred strains. When only one gene with two alleles influences the
phenotype, the expected genetic composition of the F2 population
will be AA, 25%; Aa, 50%; aa, 25%. From the foregoing,
this leads to a phenotypic mean of
¼ da + ½ ha
- ¼ da = ½ ha
(6)
(m is set at zero by a simple shift of the measurement scale). The
sum of squares of deviations from the mean then equals
½ da2 + ¼ ha2
(7)
In the absence of epistasis and linkage, the contribution of a number of
genes (k) to the F2 variance becomes
½
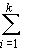 di2
di2
+ ¼
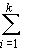 hi2
hi2
(8)
½ D + ¼ H
(9)
for ease of representation. The total phenotypical variance of an F2
is thus
VP = ½ D + ¼ H
+ E
(10)
By using groups with different genetic compositions it will be possible
to obtain estimates for the three parameters D, H, and E.
From these parameters we may then estimate the proportion of the phenotypical
variance due to additive-genetic effects, the heritability in the narrow
sense
h2n = (½ D)/VP
(11)
and the proportion of the phenotypical variance due to all genetic effects,
the heritability in the broad sense
h2b = (½ D + ¼
H)/VP
(12)
When investigating populations other than an F2 between two
inbred strains (such as a diallel cross), allele frequencies need not be
identical. Using u to indicate the frequency of the increaser allele
and v as the frequency of the decreaser allele (with u = 1 -
v) we may amend the definitions of D and H as follows:
D = ½
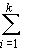
4
uividi2
(13)
and
H = ¼
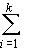
4
uivihi2
(14)
(Formally, this definition of H should be called H1,
to distinguish it from H2, the other one of the two diallel
forms of H; see [30]).
It should be noted that because D and H represent summations
of the squared effects of single genes, they can only be zero if additive-genetic
effects or dominance, respectively, are absent. This is in obvious contrast
to [d] and [h].
The crossbreeding designs employed most often in neurobehavioral genetic
studies are the classical Mendelian cross and the diallel cross (for other
possible designs, see chapter 10 and [7]). The former consists of two inbred
strains and, at least, their F1 and F2, often supplemented
with backcrosses of the F1 with both parentals. The latter consists
of a number of inbred strains (at least 3), that are crossed in all possible
combinations. The two designs render different types of information on
the genetic architecture of a trait. The classical cross permits very detailed
genetic analyses and the detection of very small genetic effects, but on
a very restricted sample of two inbred strains, only. Furthermore, it is
very hard and almost always outright impossible, to distinguish between
directional and ambidirectional dominance when using this design, because
a significant parameter [h] only indicates that dominance is present
and, at least, not completely balanced. In fact, a classical Mendelian
cross is, generally speaking, only useful if one wants to establish whether
the difference between two inbred strains is determined by either one gene
or by more genes. In contrast, the analysis of a diallel cross renders
information on a larger genetic sample and is therefore much more generalizable,
but this carries a price in that the information obtained is less detailed.
A great advantage, however, is the possibility to distinguish between ambi-
and unidirectional dominance. To uncover the genetic architecture of a
trait the diallel cross will be nearly always the design of choice.
When results from different crosses are available, it should be realized
that comparing them is not very informative. Obviously, different
results may be obtained depending on the genetic make-up of the parental
strains used, especially if the crossbreeding design employed has a low
generalizability (e.g., the classical cross). However, such results may
be combined in order to provide a more complete and generalized
picture of the genetic architecture of a trait. For instance, if one crossbreeding
experiment indicates dominance in the direction of, say, high expression
of the trait, but another cross indicates dominance in the opposite direction,
then this constitutes prima-facie evidence for ambidirectional dominance.
In fact, the presence of directional dominance may only be inferred if
all available evidence indicates that dominance is acting in the same direction.
2.3. EXAMPLES
Crusio and van Abeelen [14] addressed the question of what exactly is the
adaptive value of various mouse exploratory behaviors carried out in novel
surroundings. As one result of exploration is the collection of new, or
the updating of previously acquired, information, we argued that, if an
animal enters a completely novel environment, it is obviously of prime
interest to collect as much information as possible in a short time. On
the other hand, high exploration levels will render the animal more vulnerable
to predation. Taken together, we hypothesized an evolutionary history of
stabilizing selection for exploration. This hypothesis was subsequently
confirmed by the results of several crossbreeding experiments [11, 14]
that revealed genetic architectures comprising additive genetic variation
and/or ambidirectional dominance for most behaviors displayed in an open-field.
The above reasoning is, of course, not specific for the species mouse.
Indeed, Gerlai et al. [21] found similar genetic architectures for
exploration in an open field in a diallel cross between inbred strains
of Paradise Fish, Macropodus operculatus.
3. Phenogenetic Aspects of Causation
3.1. THE CORRELATIONAL APPROACH: BRAIN LESIONS AND
THE LOCALITY ASSUMPTION
When a behavioral neuroscientist wants to investigate the function of some
brain system, he will often do so by manipulating the system in question.
Brain lesions or pharmacological interventions to impair the functioning
of the structure of interest are among the most often used techniques.
Recently, Farah [18] reviewed the problems connected with the use of the
so-called locality assumption, that more or less equalizes the function
of an impaired structure with the defects exhibited by the damaged brain
and which is almost always invoked to interpret the results of interventionist
studies. In an elegant way, Farah [18] provided evidence that this reasoning
may lead to false conclusions. An additional disadvantage of interventionist
studies is related to the fact that large interindividual differences in
brain structure exist. This heritable variation of the brain is an aspect
that many neuroscientists tend to ignore, most likely at their own peril.
For example, widely divergent behavioral effects of septal [15, 16] or
limbic-system lesions [1], or of pharmacological interventions in the hippocampus
[38] have been reported in mice, depending on which particular inbred strain
was being used.
It appears that, in the field of neurobehavioral genetics, an alternative
approach that does not suffer from these drawbacks exists: using genetic
methods exploiting naturally occurring individual differences as a tool
for understanding brain function. No brain is like another and every individual
behaves differently. The assumption that there is a link between the variability
of the brain and individual talents and propensities seems quite plausible.
This approach differs from the usual one in neuropsychology in two important
aspects. First, no subjects are studied that, by accident or by design,
have impaired or damaged brains. Rather, all subjects fall within the range
of normal, non-pathological variation (provided animals carrying deleterious
neurological mutations are excluded). Second, instead of comparing a damaged
group with normal controls, we study a whole range of subjects and try
to correlate variation at the behavioral level with that at the neuronal
level.
This non-invasive strategy is reminiscent of the phrenological approach
propagated by Franz Josef Gall (1758-1828); Lipp has coined the name "microphrenology"
for it [28]. It appears that, as long as variation in one neuronal structure
is independent of that in another, there will be no need for a locality
assumption to interpret results of experiments carried out along these
lines. Especially when used in combination with methods permitting the
estimation of genetic correlations [7, 8], this strategy yields a very
powerful approach.
3.2. Genetic Correlations
A weakness inherent in correlational studies is that a phenotypical correlation
between characters does not necessarily reflect a functional relationship.
On the other hand, if two independent processes, one causing a positive
relationship, the other causing a negative relationship, act simultaneously
upon two characters, the effects may cancel each other so that no detectable
correlation can emerge.
These problems can largely be avoided by looking at the genetic
correlations, that is, at correlations between the genetic effects that
influence certain characters. Such correlations are caused either by genes
with pleiotropic effects or by a linkage disequilibrium. With linkage disequilibrium
we mean situations where certain allele combinations at closely linked
genes are more frequent than might be expected based on chance. This will
occur, for instance, in F2 crosses between two inbred strains
(or populations derived therefrom, such as Recombinant Inbred or Recombinant
Congenic Strains).
By using inbred strains that are only distantly related, the probability
that a linkage disequilibrium occurs may be minimized so that a possible
genetic correlation will most probably be caused by pleiotropy, that is,
there exist one or more genes that influence both characters simultaneously.
Thus, for these characters, at least part of the physiological pathways
leading from genotype to phenotype must be shared and a causal, perhaps
also functional, relationship must exist. It is this special property that
makes the genetic-correlational approach such a uniquely valuable addition
to the behavioral neuroscientists' toolbox. It should perhaps be noted
at this point (as stated by Carey [5] and to be seen easily from the equations
below) that the inverse need not be true: that is, the genetical correlation
can still be low or even zero although pleiotropic genes are present.
3.3. Theoretical Background
In the univariate analysis, we may partition the phenotypic variation into
its components E, D, and H, the environmental, additive-genetic,
and dominance contributions. In the bivariate analysis, the covariation
between two traits x and y is partitioned into its equivalent
components Exy, Dxy, and Hxy.
We may define the latter two parameters as:
Dxy = ½
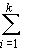
4
uividxidyi
(15)
and
Hxy = ¼
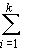
4
uivihxihyi
(16)
where dxi and dyi are the additive-genetic
effects of the ith gene on characters x and y, respectively,
and hxi and hyi are the respective
dominance deviations due to the ith gene. Evidently, only genes
that have effects on both of the characters x and y
contribute to the genetic covariance terms, whereas all genes that affect
either x or y contribute only to the respective genetic variance
terms. Combining these components of the covariance with the components
of the variance obtained in the univariate analyses we may estimate genetic
correlations as follows:
rD =
Dxy/
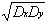
(17)
and
rH =
Hxy/
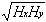
(18)
As is the case with normal correlations, genetic correlations are bound
by -1 and 1. If a genetic correlation equals unity, then all genes affecting
character x also affect character y with gene effects on
both characters being completely proportionally. A genetic correlation
will become zero only in case no gene at all affects both characters simultaneously
or in some balanced cases. For instance, if the effects of genes on character
x are uncorrelated to the effects on character y (so that
some genes influence both characters in the same direction whereas others
do so in opposite directions)[5]. Obviously, similar observations can be
made about rE, the correlation between environmental
effects on two phenotypes x and y.
In principle, every breeding design allowing the partitioning of variation
also enables one to partition covariation. However, in practice some designs
turn out to be not very well suited to estimating genetical correlations.
Especially the classical cross is very problematic in this respect and
although many examples exist in the literature in which authors claim to
have analyzed genetic correlations with this design, none really have done
so. The problem appears to be mainly due to the frequent occurrence of
the phenomenon, first observed by Tryon [36], that the variance of a segregating
F2 population is not significantly larger than those of non-segregating
populations (in extreme cases, it will even be smaller). Several possible
explanations have been brought forward. Firstly, Hall [23] attributed the
Tryon effect to an insufficient degree of inbreeding of Tryon's selected
(but not inbred) strains. Of course, this would enlarge the genetic variation
within the parental and F1 generations, but one would still
expect the F2 to have a somewhat larger variance. In addition,
the Tryon effect has since also been observed in crosses between highly
inbred strains. A second explanation was presented by Hirsch [26]. He argued
that most phenotypes are influenced by more than one gene. If we take the
rat, with a karyotype of 21 chromosome pairs, as an example and, for simplicity,
treat these chromosomes as major indivisible genes, one can see that this
organism can produce 221 different kinds of gametes, leading
to 321 (= 1.05 x 1010) different possible genotypes.
In reality, this number will be even larger because chromosomes are not
indivisible. Obviously, no experiment can take from an F2 generation
a sample large enough to have all these genotypes represented and Hirsch
[26] assumed this sampling effect to lower the observed F2 variances
below expected levels. Tellegen [34] quite correctly countered that as
long as the sampling from the F2 is random, an unbiased estimate
of the population variance should be obtained. In addition, it can easily
be seen that even if Hirsch's reasoning were correct, the F2
variance would still be expected to significantly exceed that of non-segregating
generations, being the sum of environmentally-induced variation and, in
his reasoning, at least some genetic variation.
Bruell [3] had observed that the amount of variance caused by segregation
in the F2 increases if gene effects are larger and decreases
if more genes influence the phenotype studied (cf. equations 13 and 14).
If environmental influences on the phenotype are large, an extremely large
sample would be needed to detect the difference in variance between the
F2 and F1 populations at a sufficient level of significance
in situations with many genes and relatively small gene effects. As sample
sizes are limited by considerations of time, money, and space, while environmental
influences on behavioral characters are usually very pronounced, one should
normally expect F2 variances not to differ significantly from
F1 variances. Due to sampling error, they may then even be smaller,
although usually not significantly so. Homeostatic processes may be responsible
if the latter situation occurs [27].
The problem therefore boils down to one of statistical power. It should
be recalled here that larger sample sizes are needed to obtain accurate
estimates of the variance of a population than for estimating its mean.
By analogy, this also goes for covariances. In sum, unless rather huge
sample sizes are used, classical crosses will generally lack the statistical
power needed to accurately estimate genetical correlations.
Another reason that the classical cross is less suited for bi- and multivariate
studies is the fact that results are not generalizable, but based on a
restricted sample of two inbred strains only: even if genetic correlations
would be estimated correctly with this design (see [24] for appropriate
statistical methods), there exists a not negligible probability that they
would be due to a linkage disequilibrium instead of pleiotropy. Of course,
it is exactly the latter property that researchers employ when localizing
genes. Note, however, that this is a special case in which one character,
the molecular marker, is completely determined by the genotype (see also
the following section).
A more suitable method is the diallel cross, for which a bivariate extension
is available [8], whereas an interesting shortcut is offered by using a
panel of inbred strains. Correlations between strain means either permit
the estimation of additive-genetic correlations (using the methods described
in [25]), or provide a direct lower-bound estimate of additive-genetic
correlations (if the traits to be correlated have been measured in different
individuals from these strains).
From the foregoing, it may easily be seen that the variance of the means
of a set of inbred strains equals
D + E/n (19)
where n is the harmonic mean of the number of subjects per strain. The
covariance between the means obtained for two characters x and y
can then be expressed as
Dxy + Exy/n
(20a)
in case both characters are being measured on the same individuals or as
Dxy
(20b)
in case characters x and y are being measured on different
individuals from the same strains. The correlation between the strain means
in these two situations will now equal
(
Dxy +
Exy/
n)/
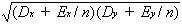
(21a)
Dxy/
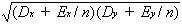
(21b)
respectively. Especially if environmental effects are small and large numbers
of subjects are being used, the correlation between inbred strain means
will approach the genetical correlation. In addition, it can easily be
seen that equation 21b will always render a lower-bound estimate of the
genetical correlation, even if n is small or if environmental effects
are large. It should be realized that equation 21a may render a significant
correlation even in the complete absence of any genetical effects. In the
latter case, equation 21a reduces to the environmental correlation. By
using the within-strain variation and covariation as estimates of the environmental
variances and covariances, respectively, equations 19 and 20 render unbiased
estimates of environmental and genetical correlations for both cases (for
more details, see [25]).
Recombinant inbred strains (RIS) have sometimes also been used to estimate
genetic correlations between phenotypes, using the above-described methods
for correlations using ordinary inbred strains. It should be realized,
however, that there is a considerable risk that any genetic correlations
thus found will be due to a linkage disequilibrium because RIS have been
derived from an F2 between two inbred strains. As was the case
with the classical cross itself, this property is of course of interest
for researchers hoping to localize QTL (but see ch. 3.3.3).
Except in the case of correlations between inbred strain means, testing
the significance of genetic correlations is often problematic and the power
of available tests is not yet well known at this moment. Fortunately, when
the environmental and genetic correlations are used as input for further,
multivariate, analyses, the possible significance or lack thereof of an
individual correlation is no longer very important.
3.4. EXAMPLES
3.4.1. Rearing behavior in an open-field and hippocampal
mossy fibers in mice
Crusio et al. [12] carried out a diallel cross study in which 5 different
inbred strains were crossed in all possible ways. In 150 male mice from
the 25 resulting crosses they measured the rearing-up frequency during
a 20 min session in an open field and the extent of the hippocampal intra-
and infrapyramidal mossy fiber projection (IIPMF). They obtained a marginally
significant phenotypical correlation of 0.138 (df = 148, 0.05 < P
< 0.10). Ordinarily, one would take such a result as evidence that variations
in the size of the IIPMF is not related to behavioral variation. However,
a quantitative-genetic partitioning of the covariation showed that the
genetic correlation was quite sizable: 0.479. The low phenotypical correlation
was explained by the modest heritability for rearing (0.25 Vs 0.53 for
the IIPMF [10]) and by the fact that the (low) environmental correlation
had a sign opposite to that of the genetic correlation. The genetic relationship
between rearing, on the one hand, and the IIPMF, on the other hand, was
confirmed by the finding that a line selected for high rearing frequency
had larger IIPMF projections than a line selected for low rearing frequencies
[13], exactly as would be predicted from a positive genetic correlation
between these characters. From these data, it was concluded that the IIPMF
play an important role in the regulation of open-field rearing [9].
3.4.2. Nerve conduction velocity and IQ in man
Lately, human behavior geneticists have also started to use genetic correlations
to uncover brain-behavior relationships, especially the very active group
around Dorret Boomsma at the Free University of Amsterdam (The Netherlands).
In a recent experiment they used the twin method (see chapter 12) to examine
the possible existence of a genetic correlation between speed-of-information
processing (SIP) and IQ [33]. It was postulated that SIP, as derived from
reaction times on experimental tasks, measures the efficiency with which
subjects can perform basic cognitive operations underlying a wide range
of intellectual abilities. Phenotypic correlations generally range from
–0.2 to –0.4. Rijsdijk et al. [33] showed that genetic correlations also
fell in this range at ages 16 and 18 years, whereas environmental correlations
were essentially zero. A common, heritable biological basis underlying
the SIP-IQ relationship is thus very probable.
3.4.3. Localization of QTL
Currently, Recombinant Inbred Strains are widely used as a tool to localize
QTL. Unfortunately, problems of statistical power (often also due to multiple
testing) lead to many false positives and negatives, as illustrated by
the studies of Mathis et al. [31] and Gershenfeld et al. [22]. In the first
study, a number of QTL associated with open-field behavior were "identified"
using a large set of RIS between the inbred mouse strains C56BL/6J and
A/J. In the second one, an F2 generation between these same
inbred strains was studied, again leading to the "identification" of a
number of QTL for the same behavioral phenotypes. However, none of the
QTL found was common to both studies, aptly demonstrating the lack of reliability
of current QTL methods.
4. Some common misapplications
A final point of caution is at its place here. Quantitative-genetic
methods are not only used, but also, unfortunately, regularly abused. One
problem already addressed above concerns whether information obtained at
one level (on the components of means, say) can render information about
another level (on the components of variance or covariance, for instance).
This is sometimes the case, sometimes not. A few frequently made mistakes
are mentioned here.
I. If some genetic effects are found for one character but not for
another, this implies that these characters are influenced by different
genes. Wrong! The equations given above should already make it abundantly
clear that this is not true. An example may illustrate this.
Albinism in mice, for instance, is a character that is completely recessive
as far as coat color is concerned. A quantitative-genetic analysis would
indicate the significant presence of both d and h of equal
size, in such a way that the heterozygote would completely resemble the
non-albino homozygote. However, if we now would perform a quantitative-genetic
analysis of the phenotype "activity of the enzyme tyrosinase", we would
find that dominance is completely absent for this character, the heterozygote
being completely intermediate between the two homozygotes. Still, as we
know very well, only one and the same gene is involved here, which acts
as a recessive on the level of coat color but shows intermediate inheritance
on the level of the activity of the responsible enzyme.
In fact, only the presence of a genetic correlation between two phenotypes
provides evidence that (a) gene(s) is (are) simultaneously influencing
both. As was pointed out above, the reverse need not be true.
II. If two characters are correlated between two parental strains
but not in their F2, they segregate independently and, hence,
are influenced by different genes (in other words, there is no genetic
correlation between them). Wrong! In fact, this observation may be true,
but in only one exceptional situation: if at least one of the characters
we are dealing with (for instance, a molecular-genetic marker) is completely
determined by the genotype. This latter condition is called complete penetrance
or, in quantitative-genetic terms, the heritability in the broad sense
is said to equal 1. For behavioral and neural phenotypes, this condition
almost never occurs. A few further observations should be made.
First, in all situations (including the above one), the phenotypical
correlation within an F2 generation will be a function of the
heritabilities of both characters and the sizes and signs of the genetic
and environmental correlations between them. If, to simplify the equation,
we suppose dominance effects to be absent for both characters x
and y, then
rP = hxhyrD
+ exeyrE
(22)
where rP is the phenotypical correlation, hx
and hy are the square roots of the narrow-sense heritabilities
of characters x and y, ex and ey
are the square roots of the "environmentalities" (the proportion of the
phenotypical variance due to the environment; ex2
= 1 - hx2), and rE is the
environmental correlation.
Equation 22 has a number of important implications. For instance, the
size and sign of rP evidently do not render any information
at all about the size and sign of rD. It can easily be
seen that a significant phenotypical correlation may even be completely
absent (rP not significantly different from zero) in
case rD and rE have opposite signs
and the absolute value of hxhyrD comes
close to that of exeyrE. In recent
years, experiments attempting to localize polygenes (called Quantitative
Trait Loci, QTL) have become ever more popular. In such experiments one
character, the molecular-genetic marker whose possible linkage to a putative
QTL is being tested, will have a heritability of 1 and zero environmentality.
In such a case, equation 22 reduces to
rP = hxrD
(23)
This latter equation implies that there is an upper bound to the correlation
between a behavioral or neural phenotype, on the one hand, and a marker
locus, on the other hand, even if this marker locus would not just be
linked to the hypothetical QTL but actually be identical with it. Equation
23 explains why, especially when heritabilities are low (and also because
of the lack of statistical power of estimates of variance and covariance
in F2 populations referred to in section 3.3), the power to
reliably detect QTL is often very low, leading to many false positives
and negatives [32]).
Second, note that in the above erroneous statement the words "between
two parental strains" were used. The correlation within such
strains has obviously no bearing at all on the eventual presence or absence
of genetic correlations. As all individuals within inbred strains have
the same genotype, any correlations occurring within such a strain are
of environmental origin, of course. This is not to say, of course, that
at any given point in time, two individuals belonging to the same inbred
strain may not have different profiles of gene expression. If such is the
case, however, then such differences in gene expression itself must be
due to environmental influences (assuming, of course, that both individuals
are at similar stages of development).
III. To determine the heritability of a character one should carry
out a selection study.
This proposition is perhaps formally not incorrect (heritabilities can
be derived from selection studies), but it contains in fact two conceptual
errors. The first one is that there is some information to be gained from
a heritability coefficient. Actually, except as an intermediate step in
estimating genetic correlations, heritabilities do not have any intrinsic
value. The only interesting facts about heritabilities are whether they
differ significantly from zero (meaning that there is significant genetic
variation) or from unity (meaning that there is significant environmental
variation). There is one further use of heritability estimates, which is
that their size predicts the eventual effects of selection pressures (whether
artificial or natural [16]). This second conceptual error derives from
this fact: once a selection study has been carried out and selection has
led to the successful establishment of divergent lines, knowledge about
heritability become more or less useless: it is not interesting any more
to determine whether selection might be successful! Thus, there is only
a single situation in which one would perform a selection experiment to
estimate heritabilities: when one wishes to estimate genetic correlations
and for some reason inbred strains are not available.
5. Conclusion
In conclusion, if the above pitfalls are avoided, quantitative-genetic
experiments can render valuable information on the genetic architecture
of a trait. In addition, they can provide information about the multivariate
genetic structure of complexes of traits. Because of this last property,
quantitative genetics may serve as a valuable additional tool in the neuroscientist's
arsenal and may greatly enhance our understanding of the genetic and neural
mechanisms underlying individual differences in behavior.
6. Acknowledgments
The preparation of this manuscript was supported by the Centre National
de la Recherche Scientifique (UPR 9074), Ministry for Research and Technology,
Région Centre, and Préfecture de la Région Centre.
UPR 9074 is affiliated with INSERM and the University of Orléans.
This chapter is dedicated to the memory of my teacher, mentor, and dear
friend, Hans van Abeelen (1936-1998).
7. References
-
AMMASSARI-TEULE M, FAGIOLI S, ROSSI-ARNAUD C: Genotype-dependent involvement
of limbic areas in spatial learning and postlesion recovery. Physiol Behav,
1992, 52:505-510
-
BROADHURST PL, JINKS JL: What genetical architecture can tell us about
the natural selection of behavioural traits. In JHF van Abeelen (Ed): The
Genetics of Behaviour. North-Holland, Amsterdam, 1974, pp 43-63
-
BRUELL JH: Dominance and segregation in the inheritance of quantitaitve
behavior in mice. In EL Bliss (Ed): Roots of behavior. Hoeber and Harper,
New York, 1962, pp 48-67
-
CAMHI JM: Neural mechanisms of behavior. Curr Opinion Neurobiol, 1993,
3:1011-1019
-
CAREY G: Inference about genetic correlations. Behav Genet, 1988, 18:329-338
-
CRUSIO WE: HOMAL: A computer program for selecting adequate data transformations,
J Hered, 1990, 81:173
-
CRUSIO WE: Quantitative Genetics. In D Goldowitz, D Wahlsten, R Wimer (Eds):
Techniques for the Genetic Analysis of Brain and Behavior: Focus on the
Mouse. Techniques in the Behavioral and Neural Sciences, Volume 8, Elsevier,
Amsterdam, 1992, pp 231-250
-
CRUSIO WE: Bi- and multivariate analyses of diallel crosses: A tool for
the genetic dissection of neurobehavioral phenotypes. Behav Genet, 1993,
23:59-67
-
CRUSIO WE: Natural selection on hippocampal circuitry underlying exploratory
behaviour in mice: Quantitative-genetic analysis. In E Alleva, A Fasolo,
H-P Lipp, L Nadel, L Ricceri (Eds): Behavioural Brain Research in Naturalistic
and Seminaturalistic Settings. NATO Advanced Study Institutes Series D,
Behavioural and Social Sciences, Kluwer Academic Press, Dordrecht, Pays-Bas,
1995, pp 323-342
-
CRUSIO WE, GENTHNER-GRIMM G, SCHWEGLER H: A quantitative-genetic analysis
of hippocampal variation in the mouse. J Neurogenet, 1986, 3:203-214.
-
CRUSIO WE, SCHWEGLER H, VAN ABEELEN JHF: Behavioral responses to novelty
and structural variation of the hippocampus in mice. I. Quantitative-genetic
analysis of behavior in the open-field. Behav Brain Res, 1989, 32:75-80.
-
CRUSIO WE, SCHWEGLER H, VAN ABEELEN JHF: Behavioral responses to novelty
and structural variation of the hippocampus in mice. II. Multivariate genetic
analysis. Behav Brain Res, 1989, 32:81-88.
-
CRUSIO WE, SCHWEGLER H, BRUST I, VAN ABEELEN JHF: Genetic selection for
novelty-induced rearing behavior in mice produces changes in hippocampal
mossy fiber distributions. J Neurogenet, 1989, 5:87-93.
-
CRUSIO WE, VAN ABEELEN JHF: The genetic architecture of behavioural responses
to novelty in mice. Heredity, 1986, 56:55-63.
-
DONOVICK PJ, BURRIGHT RG, FANELLI RJ, ENGELLENNER WJ: Septal lesions and
avoidance behavior: Genetic, neurochemical and behavioral considerations.
Physiol Behav, 1981, 26:495-507
-
FALCONER DS, MACKAY TFC: Introduction to Quantitative Genetics. 4th Edition.
Longman Group Ltd, Harlow, Essex, 1996
-
FANELLI RJ, BURRIGHT RJ, DONOVICK PJ: A multivariate approach to the analysis
of genetic and septal lesion effects on maze performance in mice. Behav
Neurosci, 1983, 97:354-369
-
FARAH MJ: Neuropsychological inference with an interactive brain: A critique
of the "locality" assumption. Behav Brain Sci, 1994, 17:43-104
-
FISHER RA: The correlation between relatives on the supposition of Mendelian
inheritance. Trans R Soc Edinb, 1918, 52:399-433
-
FRYER G, ILES TD: The Cichlid Fishes of the Great Lakes of Africa: Their
Biology and Evolution. Oliver and Boyd, Edinburgh, 1972
-
GERLAI R, CRUSIO WE, CSÁNYI, V: Inheritance of species-specific
behaviors in the paradise fish (Macropodus opercularis): A diallel
study. Behav Genet, 1990, 20:487-498.
-
GERSHENFELD HK, NEUMANN PE, MATHIS C, CRAWLEY JN, LI X, PAUL SM: Mapping
quantitative trait loci for open-field behavior in mice. Behav Genet, 1997,
27:201-210
-
HALL CS: The genetics of behavior. In SS Stevens (Ed): Handbook of Experimental
Psychology, John Wiley and Sons, New York, USA, 1951, pp 304-329
-
HAYMAN BI: Maximum likelihood estimation of genetic components of variation.
Biometrics, 1960, 16:369-381
-
HEGMANN JP, POSSIDENTE B: Estimating genetic correlations from inbred strains.
Behav Genet, 1981, 11:103-114
-
HIRSCH J: Behavior-genetic, or "experimental," analysis: The challenge
of science versus the lure of technology. Am Psychol, 1967, 22:118-130
-
HYDE JS: Genetic homeostasis and behavior: Analysis, data, and theory.
Behav Genet, 1973, 3:233-245
-
LIPP HP, SCHWEGLER H, CRUSIO WE, WOLFER D, LEISINGER-TRIGONA M-C, HEIMRICH
B, DRISCOLL P: Using genetically-defined rodent strains for the identification
of hippocampal traits relevant for two-way avoidance learning: A non-invasive
approach. Experientia, 1989, 45:845-859
-
MATHER K: The Genetical Structure of Populations. Chapman and Hall, London,
1973
-
MATHER K, JINKS JL: Biometrical Genetics, 3rd ed., Chapman and
HAll, London, UK, 1982
-
MATHIS C, NEUMANN PE, GERSHENFELD H, PAUL SM, CRAWLEY JN: Genetic analysis
of anxiety-related behaviors and responses to benzodiazepine-related drugs
in AXB and BXA recombinant inbred mouse strains. Behav Genet, 1995, 25:557-568
-
MELCHINGER AE, UTZ FH, SCHÖN CC: Quantitative trait locus (QTL) mapping
using different testers and independent population samples in maize reveals
low power of QTL detection and large bias in estimates of QTL effects.
Genetics, 1998, 149:383-403
-
RIJSDIJK FV, VERNON PA, BOOMSMA DI: The genetic basis of the relation between
speed-or-information-processing and IQ. Behav Brain Res, 1998, 95:77-84
-
TELLEGEN A: Note on the Tryon effect. Am Psychol, 23:585-587
-
THODAY JM: Disruptive selection. Proc R Soc Lond B, 1972, 182:109-143
-
TRYON RC: Genetic differences in maze learning ability in rats. Yrbk Natl
Soc Stud Educ, 1940, 39:111-119
-
VAN ABEELEN JHF: Ethology and the genetic foundations of animal behavior.
In JR Royce, LP Mos (Eds): Theoretical Advances in Behavior Genetics. Sijthoff
and Noordhoff, Alphen aan den Rijn, 1979, pp 101-112
-
VAN ABEELEN JHF: Genetic control of hippocampal cholinergic and dynorphinergic
mechanisms regulating novelty-induced exploratory behavior in house mice.
Experientia, 1989, 45:839-845