Citation:
Goel, V. (1991). Notationality and the Information Processing Mind. Minds and Machines, Vol. 1, pp. 129-165.
 
 

Cognitive science uses the notion of computational information processing to explain cognitive information processing. Some philosophers have argued that anything can be described as doing computational information processing, and if so, it is a vacuous notion for explanatory purposes.

An attempt is made to explicate the notions of cognitive information processing and computational information processing and to specify the relationship between them. It is demonstrated that the resulting notion of computational information processing can only be realized in a restrictive class of dynamical systems called physical notational systems (after Goodman's theory of notationality), and that the systems generally appealed to by cognitive science -- physical symbol systems -- are indeed such systems. Furthermore, it turns out that other alternative conceptions of computational information processing, Fodor's (1975) Language of Thought and Cummins' (1989) Interpretational Semantics appeal to substantially the same restrictive class of systems.
The necessary connection of computational information processing with notationality saves the enterprise from charges of vacuousness and has some interesting implications for connectionism. But unfortunately, it distorts the subject matter and entails some troubling consequences for a cognitive science which tries to make notationality do the work of genuine mental representations.
 
 

Key Words: Computation, Cognition, Representation, Information Processing, Physical Symbol Systems, Language of Thought
 
 
 

1.0 Introduction

The goal of cognitive science is to explain intelligent human behavior. It differs from past such endeavors in viewing the organism as an information processing system, that is, a system whose behavior is to be accounted for by what it knows about the world. The underlying assumption is that the organism constructs and maintains representations of its environment, and that these representations are causally efficacious in the production of behavior. Thus the claim is that only accounts which appeal to the mental content or knowledge of the organism, and implicate that content in the explanation of behavior, will capture the right generalizations (Pylyshyn, 1984).

Many cognitive scientists propose to explain cognitive information processing in terms of computational information processing in physical symbol systems. The idea seems to be that while the two are not identical, there is sufficient similarity between them such that the latter can give us some explanatory leverage on the former. The first part of this paper is devoted to clarifying these two notions and exploring the precise sense in which the latter is supposed to explain the former.

The concept of cognitive information processing is examined. The strategy is to embed the notion in some intuitions from our folk psychology and to propose a set of constraints C which any theory will have to satisfy if it is to be a theory of cognitive information processing. The notion of computational information processing is also examined. Again the strategy is to start with some intuitions, this time those of practitioners, and to develop and explicate them along reasonably well accepted lines. It is argued that while computational systems can not satisfy the set of constraints C on cognitive information processing, they can satisfy a set of constraints C' which may be (loosely) considered the epistemic counterparts of the cognitive constraints. The claim is made that this set of constraints captures our intuitive notion of computational information processing.

There is however a very old and damaging objection made against the computational information processing story which has never been successfully answered by its advocates. It has been raised by Searle (1984) among others, and can be stated as follows: The notion of semantic content which emerges from computational information processing is very cheap. It is attributed to the system by the programmer. But if computational content is simply for the attributing, what is to prevent one from attributing it to any dynamical system? And if it can be attributed to any dynamical system, wherein lies its explanatory force? It would seem to be a rather vacuous notion.

The major goal of this paper is to provide an answer to this objection by demonstrating that the set of constraints C' can only be satisfied by a very restrictive class of physical dynamical systems called physical notational systems (after Goodman's theory of notationality); and that the "classical" (physical symbol system) architectures postulated by cognitive science are indeed physical notational systems and thus immune to the charge of vacuousness.

Furthermore, it turns out that the appeal to physical notational systems is independent of the particular constraints I place on information processing. A majority of the notationality constraints are also entailed by Cummins' (1989) Interpretational Semantics and Fodor's (1975) Language of Thought, both of which are motivated on slightly different grounds. The discussion also has some interesting implications for connectionism.

The general conclusion will be that cognitive science is trying to make notationality do the work of genuine mental representations. While this saves us from the charge of vacuousness, unfortunately it does do some damage to the subject matter. The paper concludes by noting some of the difficulties and suggesting some avenues of exploration.

2.0 Motivating the Computational Information Processing Story

2.1 From Folk Psychology to Cognitive Science
There is a certain type of explanation of human behavior which, not only gets much mileage in our day to day interactions with each other, but also embodies some very deeply held intuitions about the human mind. I am of course referring to what is variously called "folk psychology", "belief-desire psychology", or "intentional psychology". It is invoked to explain everything from why I just took a drink of water, to why 50,000 people converged on Candlestick Park on October 17, 1989, to why World War II occurred. An explanation within this framework takes the following well known form:
John believed that the 3rd game of the 1989 World Series would be played at Candlestick Park at 5:00pm on Oct. 17.

John believed that he could witness this game if he was at Candlestick Park at 5:00pm on Oct. 17, 1989.

John desired that he witness this baseball game.

Therefore John was at Candlestick Park at 5:00pm on Oct. 17, 1989.

This explanatory form requires an ontological commitment to four distinct and independent elements:¹

(E1) persons/agents (e.g. John),

(E2) a set of attitudes or psychological states (e.g. believes, desires),

(E3) the propositional content of the psychological states (e.g. "that he witness this baseball game"), and

(E4) an appeal to (i) the psychological state and (ii) its content in the explanation of behavior.

The unit of analysis for folk psychology is thus the individual agent or person. There is a relatively small set of psychological states (e.g. believe, desire, hope, fear, shame, etc.) which are attributed to the agent, and there are an infinite number of propositions which can be the content of these states. The state and the content are implicated (against background assumptions of rationality) in the explanation of the behavior. So we say that X did y because X feared that p, hoped that p, believed that p, desired that p, etc. This explanatory and predictive apparatus, with all its short comings, is the main stay of human interaction. In fact it is so deeply rooted that we are continually guilty of indiscriminately projecting it onto the world at large (i.e. anthropomorphizing rocks, trees, heavenly bodies, natural forces, etc.).

The various attempts to develop a scientifically respectable psychology can be crudely viewed as attempts to either reject this whole apparatus as a superstitious remnant of our dark untutored past or to modify, develop and systemize it until it meets the accepted standards of a scientific explanation. The behaviorists (e.g. Skinner, 1953) clearly fall into the former category while the traditional cognitivists (e.g. Wundt, in Miller, 1962) clearly fall into the latter category.

There are at least some modern cognitive scientists (e.g. Fodor, 1987) who take the whole apparatus of folk psychology quite seriously and expect it to be substantially vindicated by a scientific psychology, though they differ with traditional cognitivists in the following two regards:

(1) They would not regard the use of intentional vocabulary as satisfying or explanatory in the long run. All such talk, while "real" must ultimately be cashed out in mechanistic terms.

(2) Few of them would expect the intentional categories of folk psychology to survive intact. Most expect some degree of revision and reorganization, the extent of which is a hotly debated issue (see Churchland, 1986; Fodor, 1987).

However, most modern cognitive psychologists do not make a theoretical commitment to the first two elements (E1 and E2) of folk psychological explanations. That is, in their day to day practice, they do not use agents and psychological states such as beliefs and desires as theoretical constructs. These are not regarded as notions which can appear in explanations. They are notions which require explanation. But by the same token they do accept elements E3 and part of E4 (E4.ii). They feel perfectly justified in appealing to the representational content of psychological states and implicating that content in the explanation of behavior. This confidence comes from the belief that both of these elements (E3 and E4.ii) can themselves be explained by an appeal to computational information processing. The exact form of this explanation is the subject of the next subsection.

Here is an excerpt, randomly selected from a prominent researcher in the field of visual perception, to illustrate the point (Marr, 1979, pp.53-54):

In summary, my argument is that the 2.5-D sketch is useful because it makes explicit information about the image in a form that is closely matched to what early visual processes can deliver. We can formulate the goals of intermediate visual processing as being primarily the construction of this representation, discovering for example what are the surface orientations in a scene, which of the contours in the primal sketch correspond to surface discontinuities and should therefore be represented in the 2.5-D sketch, and which contours are missing in the primal sketch and need to be inserted into the 2.5-D sketch in order to bring it into a state that is consistent with the structure of three-dimensional space....

There are several things to note here. First, the unit of analysis is the visual system, not the organism qua agent. Thus the primal and 2.5-D sketches are constructed by and useful to the visual system, not the organism as a whole. They are actually quite inaccessible to the conscious, thinking organism. Second, both the primal sketch and the 2.5-D sketch are genuine representations with reference. For instance, "contours in the primal sketch correspond to surface discontinuities" out in the world. They can be semantically evaluated and be veridical or unveridical or true or false with respect to the world. Third, the representational content is attributed to the states of the system independent of any ascription of belief-desire psychological states. There is some mention of the "goal" of the system, but it is a device used by the theorist to communicate the explanation, rather than being part of the explanation. Fourth and finally, the system proceeds through the steps it does because it has a certain representational content and certain rules and procedures defined over that content. Thus the content is implicated in the behavior of the system.

Thus far I have been ambiguous as whether this appeal to content is logical or causal. Is the relationship of the representational states of the system at time t1 to the representational and behavioral states of the system at time t2 more similar to the relationship between premise and conclusion or the relationship between cause and effect? I do not propose to stop and seriously consider this question. Since I am at this point trying to capture the intuitions and practices of the cognitive science community, I will only note that:

(i) We generally treat the because of folk psychology as a causal because.

(ii) Several prominent cognitive scientists explicitly argue that the implication of content must be causal (Fodor, 1987; Pylyshyn, 1984; Dretske, 1989).

(iii) If the content is not causally efficacious, why do we need it? What is it for? It is generally not considered good practice to postulate unnecessary theoretical constructs.

On the basis of these observations I will conclude that some (much?) of the cognitive science community opts for the causal reading.

I take these intuitions and practices -- the appeal to the semantic content of at least some mental states and the causal implication of this content in behavior -- to be the minimal unifying theme of much of modern cognitive science. Furthermore, I take it that any theory purporting to do justice to these intuitions and practices will have to meet at least the following three constraints:

(C1) It should quantify over the semantic content of mental states.

(C2) It should causally implicate semantic content in the explanation of behavior.

(C3) It should be physically realizable.

C-Constraints on Cognitive Information Processing

I will refer to these as the C-constraints. A theory which satisfies these constraints may well be called a theory of cognitive information processing.

Much of the cognitive science community today appeals to computational information processing (in physical symbol systems) to provide a story which supposedly satisfies these constraints.² The next subsection elaborates on what this computational information processing story is supposed to be. Subsequent sections discuss and respond to some objections often raised against this story.

2.2 From Cognitive Science to Computational Information Processing

There are at least three existent claims -- the strong, the interesting, and the mediocre -- in the literature with respect to computational information processing. Each makes a different claim about the theoretical importance and role of computation in the study of cognition.

The strong version asserts an identity relation between computational states and mental states. It says that mental states are computational states and computational states are mental states. I think this is an untenable position (see Searle, 1980), and since it does not form the basis of cognitive science I will not deal with it here. The mediocre version is perhaps the most widely held. It simply says that computational vocabulary can, by analogy, be extended to cognitive phenomenon. But no attempt is made to specify the structure of the mapping. Computation is a loose, nonsubstantive, metaphor for cognition.³ This version will also not be discussed.

Much of cognitive science, however, rests on the claim that the computer is not just another metaphor for cognition. And if it is a metaphor at all, it is the last metaphor (Johnson-Laird, 1983); or more strongly, cognition is, in some literal sense, computation (Pylyshyn, 1984). This is certainly the most interesting version of the computational story and the only one I will be concerned with. On this account computation is a necessary condition on cognition. That is, cognition may be much more than computation, but it is at least computation. Having said this, the onus is on the cognitive science community to respond to the following questions:

(Qa) What exactly is computation?

(Qb) What aspects of the theory of computation are relevant to cognition?

(Qc) How does computation serve to explain cognitive capacity?

Qa What is Computation: Cognitive scientists do not have, nor should be expected to have an answer to the first question. What is computation is for the computer science community to say. Interestingly, according to some prominent computer scientists (e.g. Smith, forthcoming), there is little consensus on this key question. There are, to be sure, some loosely connected bodies of theories -- e.g. automata theory, recursive function theory, complexity theory -- that form the core of computer science, but no agreed upon understanding as to what computation is. As Smith dramatically puts it, there is no agreed upon answer to the question "what differentiates my IBM PC from my BMW?" So my remarks about computation and computational information processing should not be interpreted as being about computation-in-the-large -- whatever that may turn out to be -- but about computation as construed in the cognitive science literature (e.g. Newell and Simon, 1972; Newell, 1980; Fodor, 1975; Pylyshyn, 1984; Fodor & Pylyshyn, 1988).

Qb What Does Cognitive Science Want From Computation: As for the second question, what we want from the theory of computation is the notion of a computational information processing system.⁴ We don't really have such a story yet, but the intuition seems clear enough. We start with a story of reference and/or content in a dynamical system and extend it into a story of information processing by implicating that content in the generalizations which explain the evolution of the system through time.
 

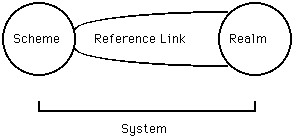
In talking about reference we are talking about a system like the one depicted in Figure 1. Such a system consists of a scheme, a realm, and a reference link.⁵ A scheme is a purely syntactic notion. It is a set of characters plus the rules of composition. The characters are the types and are instantiated in the system as tokens. The realm is the part of the world picked out and structured by scheme elements. As elements of the scheme generally pick out or comply with many elements of the realm, it is useful to introduce the notion of a reference-class or compliance-class.⁶ The reference link establishes the "connection" between the elements of the scheme and classes of elements (or their members -- depending on your metaphysics) in the realm. The system as a whole, the scheme "connected to" or "correlated with" some compliance-class or reference-class (i.e. the syntax plus the semantics), constitutes a symbol system. These additional components and relations are depicted in Figure 2.

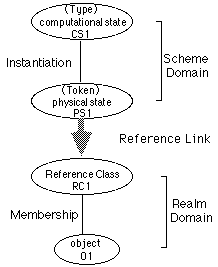
Figure 2.
 

There are a number of questions one can ask of such a system. The following five are particularly relevant for our purposes:

(Q1) What types of entities occupy the scheme domain?
(Q2) What types of entities occupy the realm domain?
(Q3) What types of reference relations exist between the scheme and realm?
(Q4) What is it by virtue of that reference is fixed?
(Q5) What is it by virtue of that content is fixed?

Here is a version of the physical symbol system story (Newell, 1980, 1987) which responds to each of the above five questions. Remember, it need not be construed as a claim about computation-in-the-large. It propounds only to do justice to "classical" cognitive science's claim on computation.

Q1 Scheme Domain: The scheme domain consists of equivalence classes of physical states to which computational states are assigned.

Q2 Realm Domain: The realm domain consists of sets or classes of (i) tokens, replicas, or instantiations of other computational states, (ii) "hard-wired" actions (such as read, write, assign, copy, delete, etc.), (iii) mathematical entities (such as numbers, functions, sets, etc.), and (iv) objects, states of affairs, actions, events, etc. in the world external to the system.

Q3 Structure of Reference Link: In the case of atomic symbols the reference link consists of computational pointers. In compound symbols or expressions reference is a function of the reference of the constitutive atomic symbols plus the rules of composition of the system.

Q4 Fixing of Reference: The reference link in Q2.i and Q2.ii is underwritten by genuine causal correlation. The reference links in the cases of Q2.iii and Q2.iv are generally fixed by the programmer and thus left unexplained by this story. However, some advocates of the story would extend it in the following way to accommodate Q2.iv: Understanding what a symbol denotes in the external world is a matter of matching up, or setting up associations between, symbols in the "language of thought" and the symbols produced by the sensory systems in the "presence of the denoted things". That is, our sensory apparatus is a transducer system. It takes as input physical stimuli impinging upon the surface extremities of the organism and produces "corresponding" or "associated" symbolic structures. These symbols are then linked to each other, and to the other symbols in the "language of thought" via computational pointers. To the extent that the reference link in Q2.iv can be explained by this story, it needs to be underwritten by causal correlation as in the case of Q2.i and Q2.ii. Finally, it is not clear how reference in the case of Q2.iii is to be explained by this story.

Q5 Fixing of Content: The content of a computational state is fixed by the network of causal reference links in which it participates.

If we extend this story of static reference and content in Figure 2 to a story of a system that dynamically evolves through time, as in Figure 3, we get a notion of a computational information processing system. The difference between the two systems is the addition of the "logical" and nomological transformation links between the instantaneous descriptions of the systems.⁷ The nomological transformation connects physical states which stand to each other in the lawful relation of cause and effect. The "logical" transformation connects computational states which are systematically related to each other. While it is inappropriate to talk about causation at this level, it is appropriate to talk about some form of logical necessity, where the exact type of transformation varies with the type of system. For example, in the predicate calculus, this relationship would be derivation; in LISP, it would be evaluation.

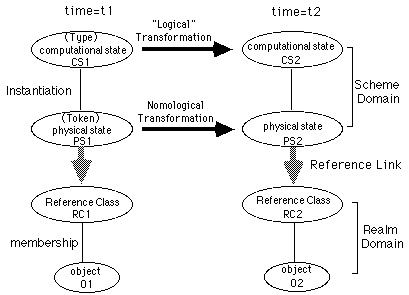
This notion of information processing supposedly allows us to take the concept of semantic content and utilize it in the explanation of behavior. The general idea is that, to the extent the physical states of the system can said to refer to, or be about, objects, events, and states of affairs, to that extent the attribution of semantic content to these states can be implicated in the behavior of the system.

Qc The Computational Mind Hypothesis: So the response to the third question -- how does the appeal to computation serve to explain cognitive capacity -- is that we can make claims about the psychology reality of the mechanisms (at an abstract level) which underwrite computational information processing. The claim would be that the mechanisms which make computational information processing possible are also necessary for the cognitive case. Much of the remainder of this paper is devoted to explicating some necessary constraints on this mechanism.

2.3 Mapping Cognitive Information Processing onto

Computational Information Processing

Having outlined the computational information processing story, the question arises, how does it satisfy the C-constraints on cognitive information processing? There are a number of the worries one might have in arguing for its relevance. In particular, there seem to be important differences in the notions of reference and content as they are used in the computational case and the human case. Reference, insofar as it is explained by computational systems is correlated with causation. But reference in general seems to outstrip causation (what ever this might mean). Certainly, causal correlation is not sufficient for reference. Furthermore, there are some traditional problems with reference, such as context dependence, opacity, fictional discourse, metaphor, etc. They seem to have no counterpart in computational systems.

There is also a difference in the notion of semantic content as it is used in the computational information processing story and as it is used in the case of human mental states (and the C-constraints). In the case of human mental states, there is always, from the first person point of view -- independent of any third person observer/interpreter -- a fact of the matter as to what the content of a given mental state is. There is no such fact for computational states. The attribution of content is always dependent or derivative on human mental states. Furthermore, if the attribution of a content is withheld from the system, its dynamical trajectory remains unaffected, strongly suggesting that, unlike the case of human mental states, the content of computational states is causally inert or epiphenomenal.

There are some who would choose to reject this distinction between human mental states and computational states (e.g. Dennett, 1987, chapter 8), but I do not think this is a serious option. I take it that the distinction is obvious, so rather than arguing about it, a more interesting issue for me is, if one accepts this distinction, if one accepts that the computational information processing story can not satisfy the C-constraints, then what exactly is its explanatory status?

I want to suggest that the classical cognitive science story rests on the intuition that certain types of computational systems can satisfy the C-constraints, if they (the C-constraints) are interpreted in the following way:

(C1') Interpret C1 as the ability to (i) assign (at the initial state of the system, t=0) a subset of the physical states of the system to computational states; (ii) correlate a subset of the computational states with compliance-classes; and (iii) once the assignments and correlations have been setup, one must be able to look at the physical states of the system and systematically recover the computational states and compliance-classes. To recover computational states means, minimally, that it is possible to identify equivalence-classes of physical states and "read off" their values. In certain cases this value will be a pointer to another computational state or device. To recover compliance-classes means, minimally, to trace through these pointers to the actual computational state or device being referred to.⁸

(C2') Interpret C2 as the ability to (i) maintain the assignment and interpretation of the system as it evolves through time; i.e. given any instantaneous description of the system one should be able to recover the computational states, the compliance classes (as above), and a pointer to the next instantaneous description in the sequence; (ii) given a temporal sequence of instantaneous descriptions it must be the case that certain physical states of the instantaneous description at t cause certain physical states and/or device activations at instantaneous description t+1; and (iii) the computational story one tells of the system must parallel the causal story.

(C3') Computation guarantees C3. (In fact it guarantees something much stronger than physical realizability; it guarantees mechanistic realizability.)

C'-Constraints on Computational Information Processing

I will refer to these as the C'-constraints. On the account I am advocating they constitute necessary constraints on computational information processing systems.

This is not an arbitrary mapping. The connection between the C-constraints and the C'-constraints is the following: In C1 (the case of human mental states) there is, from the first person point of view, a fact of the matter as to the content of a mental state, independent of any third person assignability and interpretability. There can be no such fact in the computational case. So C1' replaces this fact with another fact, that the system be such that a content can be systematically assigned to and recovered from a state of the system from a third person point of view. C2 requires that the content of mental states be causally implicated in behavior. I take it that there is a fact corresponding to this constraint in the case of human mental states. But there seems to be no such fact in the computational case. Again, C2' replaces this fact with the fact that the systematic assignability and interpretability of the instantaneous descriptions be maintained and that there be a parallelism between the causal and logical levels as one traces the trajectory of the system. One might (loosely) view the move from the C-constraints to the C'-constraints as an attempt to trade in some troublesome first person ontology for third person epistemology. Such a move that is not without precedent in psychology (e.g. behaviorism).

The satisfaction of the C'-constraints by certain computational systems is supposed to provide us with some explanatory leverage in understanding how the C-constraints might be satisfied. Very briefly, the claim is that the mechanisms which enable the satisfaction of the C'-constraints are also necessary (but not sufficient) for the satisfaction of the C-constraints.

3.0 Vacuousness Objection to Computational Information Processing

An issue which arises and needs to be dealt with at this point is the following: What exactly is necessary for the satisfaction of the C'-constraints. The issue has been raised by a number of philosophers (e.g. Searle, 1984) and leads to the following damaging objection: If computational states have an information content only in so far as there is a cognitive agent around to interpret them as such, then the sense in which they have an information content is the same sense in which the states of any physical system have an information content. And the sense in which a computational system does information processing is the sense in which every dynamical system is doing information processing. Thus the planets orbiting the sun are calculating differential equations, the trees in my yard are annually noting that they are a year older, and the water draining away from my front steps and finding its way to the storm sewers and into San Francisco Bay is doing computational information processing of immense complexity. But if anything and everything can be described as if it is doing computational information processing, then to claim that the cognitive system is a computational information processing system (because everything is a computational information processing system) is not to make a substantive empirical claim. As a point of logic it is trivially true, as an empirical claim it is vacuous.

A surprising number of researchers are simply unimpressed by this objection. They adopt the attitude that sometimes it is useful to describe a system as doing computational information processing and at other times it is not. When it is useful to do so, one should. When it is not useful, one shouldn't. One might call this the utility reply.
Others do clearly appreciate the force of the objection. Chomsky (1980) for one accepts that if everything can be described as knowing and following certain rules (in our sense of doing computational information processing), then it is not a very interesting concept. But he thinks that not every behavior is, or can be described as, rule governed behavior, and that there is a fact of the matter as to whether something falls (or does not fall) into this category. He raises the objection and responds to it in the following way (Chomsky, 1980, pp.10-11):⁹

True, there would be little point to a concept of "cognizing" that did not distinguish "cognizing the rules of grammar" from the bicycle rider's knowing that he should push the pedals or lean into a curve, given what we assume to be the facts of the matter. But it seems easy enough to make the relevant distinction. In the case of riding a bicycle, there is no reason to suppose that the rules in question are represented in a cognitive structure of anything like the sort I have described. Rather, we take bicycle riding to be a skill ... based on certain reflex systems, in which case it would be incorrect to attribute a cognitive structure ... to the person who exercises the skill.... nothing seems to be explained by attributing to the bicycle rider a cognitive structure incorporating the rules with which his practice accords. But suppose we are wrong, and in fact the bicycle rider does have a representation of certain physical principles in his mind and uses them to plan or compute his next act. In this case we should attribute to him a cognitive structure, and in fact, it would be quite appropriate to say that he cognizes these principles as he does the rules of his language. The question, I take it, is basically one of fact.

To help clarify the issue, consider two missile systems, each of which is designed to send a rocket to the moon. One of them operates along lines once proposed by B. F. Skinner; it has several pigeons looking at a screen that depicts what lies directly ahead, trained to peck when the rocket veers off course, their pecking restoring the image of the moon to a focused position on the screen. Consider, in contrast, a system that incorporates an explicit theory of the motions of the heavenly bodies and information about its initial position and velocity and that carries out measurements and computations using its internalized theory to adjust its course as it proceeds. [while the two systems may be behaviorally equivalent] .... In the second case, but not in the first, inquiry might lead us to attribute to the missile something like a "mental state".... In the first case, such an account would be factually wrong. I think that the two cases fall on opposite sides of an important divide....

While Chomsky has some suggestive intuitions here, he does not really provide us with an explicit criteria to distinguish between the two cases. The question remains, "what facts about the second case differentiate it from the first case such that we can claim it is doing computational information processing (or "cognizing" or "rule following" in Chomsky's vocabulary) and attribute "something like a 'mental state' " to it? Or alternatively, is there a principled "divide" between systems which do computational information processing (and satisfy the C'-constraints) and systems which do not? If so, what is the basis of the divide? If not, what is the explanatory force of the notion?

In the next several sections I propose to respond to these questions. I will argue that the C'-constraints are nontrivial constraints, and in fact can only be satisfied by a small subset of dynamical systems, the subset whose members are also physical notational systems (to be explained shortly). But before actually commencing the argument, it is at this point necessary to stop and review Goodman's theory of notationality from which the notion of a physical notational system is derived.

4.0 Goodman's Theory of Notationality
Nelson Goodman's (1976) Languages of Art: An Approach to a Theory of Symbols, originally published in 1968, is perhaps the deepest formal analysis of symbol systems to date. However, it remains virtually unknown and/or unappreciated in cognitive science circles.¹⁰ Given that cognitive science is in the business of explaining behavior in terms of internalized symbol systems, this is a most unfortunate oversight. In this section I will summarize Goodman's theory of notation and use it in subsequent sections to analyze and explicate the class of computational information processing systems (i.e. the class of systems which can meet the C'-constraints).

Goodman's interest in advancing the theory of notation is to develop a metric which can be used to classify and order symbol schemes and systems. He puts forward notationality as an ideal extreme towards which symbol schemes and systems may strive if they meet certain stringent criteria.
There are five independent criteria, two syntactic and three semantic. They are (i) syntactic disjointness, (ii) syntactic finite differentiation, (iii) semantic unambiguity, (iv) semantic disjointness, and (v) semantic finite differentiation. A notational scheme must meet the first two. A notational system must meet all five. When a symbol system passes the test of notationality, it brings with it a guarantee of a one to one mapping from inscription to character to the world and back again.

4.1 Syntactic Criteria

The first requirement of notationality is syntactic disjointness, where disjointness is a relationship between classes of character indifferent or syntactically equivalent inscriptions. Two inscriptions are said to be character-indifferent if "neither one belongs to any character the other does not" (p.132). This means that all marks that belong to the same character constitute an equivalence class (i.e. they satisfy the requirements of reflexitivity, symmetry, and transitivity). Thus character-indifference insures that all inscriptions of a character are "true copies" of each other, that any inscription of a character is as valid as any other inscription of that character. How it is achieved is a separate matter, though Goodman points out that it need not be by virtue of any "simple function of shape, size, etc." (p. 138).

Given two sets of character-indifferent marks, such sets must be disjoint; no mark outside of a set will be character indifferent with members of it. Or as Goodman puts it, a "character in a notation is a most-comprehensive class of character-indifferent inscriptions" (p.132). Disjointness ensures that no mark genuinely belongs to more than one character.

The second criteria for notationality is syntactic finite differentiation. Goodman states it as follows (p. 135-36):
For every two characters k and k' and every mark m that does not actually belong to both, determination either that m does not belong to k or that m does not belong to k' is theoretically possible. (italics omitted)

The phrase "theoretically possible" is rather interesting and should be immediately qualified. According to Goodman "theoretically possible" may be interpreted in "any reasonable way". For as he goes on to note, what ever the interpretation, "all logically and mathematically grounded impossibility ... will of course be excluded" (p. 136).

Finite differentiation is not dependent on a finite number of characters. There can be schemes of an infinite number of characters which are finitely differentiated (e.g. Arabic fractional notation). There can also be schemes of two characters which are not finitely differentiated (e.g. a scheme whereby all marks not longer than one inch belong to one character and all marks longer than one inch belong to the other character).

Disjointness and finite differentiation are independent requirements. The former is ontic, the latter epistemic. A scheme of straight marks in which every difference in length -- no matter how small -- counts as a difference of character is disjoint but not finitely differentiated. (It is disjoint because by definition we know that no two characters have an inscription in common. It is not finitely differentiated because it is theoretically impossible to do a mapping from the marks to the characters.) A scheme in which all the marks are perceptually different, but where two characters have at least one inscription in common is finitely differentiated but not disjoint. (It is not that the differentiation can not be made, it is simply that the inscription genuinely belongs to more than one character.) In the case of disjointness the issue is one of having equivalence classes of inscriptions which do not satisfy the requirements of intersection or inclusion. In the case of finite differentiation the issue is one of being able to theoretically specify the correspondence from inscriptions to characters.

Thus far we have been talking about atomic inscriptions and characters. Most symbol schemes have rules of composition (usually defined over categories of characters/inscriptions) which allow for the combination of atomic inscriptions/characters into compound inscriptions/characters. The above criteria of notationality works exactly the same for compound inscriptions and characters.

Jointly the two requirements are quite strong. They ensure a one to one mapping between inscriptions and characters and thus enable the collapse of the distinction between inscription and character. In a notational scheme, manipulating the inscription is identical to manipulating the character.

4.2 Semantic Criteria

The first semantic criteria of notationality is unambiguity. It applies to the correlation or compliance link. It states that every inscription must have the same, single, compliance-class in each and every instance, irrespective of context. Thus "a mark that is unequivocally an inscription of a single character is nevertheless ambiguous if it has different compliants at different times or in different contexts, whether its several ranges result from different literal or from literal and metaphorical uses" (p. 147).¹¹

A character is unambiguous if all its inscriptions are unambiguous and if they all have the same compliance-class. The common compliance-class of the inscriptions is the compliance-class of the character. This means that if a system is unambiguous, syntactic equivalence will ensure semantic equivalence. Since the inscriptions of an unambiguous character are syntactically equivalent and semantically equivalent, one can "speak of the character and its compliance-class without bothering to distinguish among its several instances" (p. 147-48).

The second semantic criteria of notationality is the disjointness or non-intersection of every two compliance-classes in the system. It stipulates that (p. 151) "no two characters have any compliant in common" (italics omitted). This is a rather severe restriction. It enforces a semantic segregation of characters in the system by disallowing such semantically intersecting terms as "doctor", "Englishman", "man", and "animal". But it does not imply discreteness of compliants. It is perfectly ok for compliants of one character to be parts of compliants of another character. Thus it is ok to have the characters 'man' and 'leg' in the system.

The final requirement for a notational system is semantic finite differentiation. It is stated as follows (p. 152): "for every two characters K and K' such that their compliance-classes are not identical, and every object h that does not comply with both, determination either that h does not comply with K or that h does not comply with K' is theoretically possible" (italics omitted). The interpretation of "theoretically possible" is as above.

An example Goodman offers is that of fully reduced Arabic fractional numerals correlated with objects, based on their weights in fractions of an ounce (p. 153). In this system, since there is no preset limit as to what constitutes a significant difference in weight, it will be the case that for many characters it will not be possible to determine that the object does not comply with them all (i.e. it will not be possible to assign a given object to a single class). Such a system meets the criteria of syntactic disjointness and finite differentiation as well as the semantic requirements of unambiguity and disjointness but fails the requirement of semantic finite differentiation. Even a system containing two characters "a" and "b", where "a" is correlated with all objects weighing a pound or less, and "b" is correlated with all objects weighing more than a pound fails semantic finite differentiation.

Goodman uses his theory of notationality to arrange and order symbol systems on the basis of which combination of the five criteria they meet or fail to meet. This allows him to engage in a fascinating and sophisticated discussion about the relationship between such diverse systems as natural language, diagrams, musical scores, paintings, etc. While this in itself has significant implications for cognitive science (Goel, 1990), here I will use the theory to derive the concept of a physical notational system, and then use this notion to gauge and constrain the class of physical dynamical systems and their interpretations which can constitute computational information processing systems.

5.0 Physical Notational Systems

Goodman, in his analysis is concerned with abstract symbol systems. Cognitive science is concerned with the physical realizations of these abstractions -- with physical symbol systems. However, Goodman's characterization of notational systems can be transformed into a characterization of physical notational systems by making some adjustments. A physical notational system is, by definition, a system which meets the following constraints:

PNS1) Equivalence classes of physical states (i.e. computational states) must be specified in terms of some function of causally efficacious characteristics such as shape or size, and these classes must be disjoint. Whereas, in Goodman's discussion of syntactic disjointness it was noted that character-indifference need not be by virtue of any "simple function of shape, size, etc.", in physical notational systems, character-indifference must be -- if not a simple function -- some function of causally efficacious characteristics such as shape or size.

PNS2) Membership of physical states in equivalence-classes which constitute computational states must be effectively differentiable, where differentiability is limited by physical possibilities. In Goodman's discussion of finite differentiation, the major concern in the interpretation of "theoretically possible" was to exclude logical and mathematical impossibilities. In the case of physical systems the "theoretically possible" must be ultimately constrained by physical possibilities, and more immediately, by our ability to devise sensory instrumentation. So a more reasonable interpretation for our purposes would be "perceptually possible" (for the relevant mechanism).

PNS3) Each state in the evolution of the system must be "causally connected in the right way". While the specification of "causally connected in the right way" is obviously problematic, the intuition is reasonably clear: Certain physical states in the instantaneous description at t_n must have a direct causal connection to certain physical states in instantaneous descriptions at t_n-1 and t_n+1. The connection must be such that certain physical states at t_n-1 cause or bring about certain physical states at t_n, which in turn bring about certain states at t_n+1, and so on. Furthermore the transformation of the computational state CS_n at t_n into CS_n+1 at t_n+1 must be realized as the causal transformation of physical state PS_n at t_n into PS_n+1 at t_n+1, where PS_n at t_n and PS_n+1 at t_n+1 are a subset of physical states of the system which are mapped onto computational states.

PNS4) The correlation of equivalence classes of physical states (i.e. computational states) with compliance-classes -- within each instantaneous description of the process -- must be unambiguous in the sense that each member of an equivalence class of physical states must have the same, single, compliance-class in each and every occurrence of that instantaneous description.

PNS5) The membership of entities in compliance-classes must be effectively differentiable.

PNS6) The transformation of the system from one instantaneous description to the next instantaneous description must be such that the above five criteria are preserved.

PNS-Constraints on Physical Notational Systems

I will refer to these as the PNS-constraints. Notice the difference between these six constraints and Goodman's original five. First, the semantic disjointness constraint has been dropped. It is not needed for the type of interpretation called for in the C'-constraints (because it is not necessary to be able to go from the referents back to the computational states). Second, since we are dealing with dynamical rather than static systems, it was necessary to add a causal constraint (PNS3) and a constraint which maintains the other five constraints across instantaneous descriptions of the system (PNS6).

All subsequent references to notational systems, whether prefaced with 'physical' or not, will be references to systems which meet these six constraints (rather than Goodman's original five constraints). References to notational schemes will be references to systems which meet constraints PNS1, PNS2, PNS3, and PNS6', where PNS6' reads "the transformation of the system from one instantaneous description to the next instantaneous description must be such that constraints PNS1, PNS2, and PNS3 are preserved".

Physical notational systems play a very special role in cognitive science because they are necessary for the satisfaction of C'-constraints on computational information processing systems. That is, if any of the PNS-constraints are violated, then some C'-constraint will be violated. For example:

(A) If the individuation of equivalence classes of physical states is not disjoint (PNS1), there will not be a fact of the matter as to which computational state some physical state belongs to, thus thwarting the assignment of computational states to physical states. This would be a violation of C1' & C2'(i).

(B) If the membership of physical states in equivalence classes of computational states is not effectively differentiable (PNS2) -- then whether the classes are disjoint or not -- no procedure will be able to effectively make the assignment of physical states to computational states. For example, if the individuation of computational states is dense, then in the assignment of physical states to computational states, there will always be two computational states such that membership of the physical state to either computational state cannot be ruled out. This would also violate C1' & C2'(i).

(C) If the correlation of computational states with compliance-classes is ambiguous (PNS4), then there will be no fact of the matter as to the referent of any given computational state, and the systematic interpretability of the system will be impaired. This would violate C1'(iii) & C2'(i). (Note however, that redundancy need not be outlawed. We can always collapse the several computational states by enlarging the equivalence class of physical states, without affecting interpretability.)

(D) If membership in compliance-classes is not effectively differentiable (PNS5), then no effective procedure will be able to specify which object any given computational state refers to. For example, if the compliance-classes are densely ordered, then in the assignment of objects to classes, there will be two classes for any object O, such that it is not effectively possible to say that O does not belong to one. This would violate C1'(ii, iii) & C2'(i)

(E) If the causal constraint is violated (PNS3) then C2'(ii, iii) will also be violated. This will lead to the absurd results that time-slice sequences of arbitrary, unconnected patterns (e.g. the conjunction of the physical states consisting of craters on the moon at t1, the meteor shower on Neptune at t2, the food on my plate at t3, the traffic pattern on the Golden Gate Bridge at t4, etc.) qualify as computational systems.

(F) If at any instantaneous description of the system, any of the above constraints are violated (PNS6), then at that point some C'-constraint will be violated.

We are now in a position to respond to the vacuousness charge by showing that the class of physical notational systems is not coextensive with the class of physical dynamical systems -- i.e. not every law governed process can be accurately described as a computational information processing system.

5.1 Physical Notational Systems are Subset of Physical Dynamical Systems

In this subsection I want to argue for the ontological reality of physical notational schemes and systems and suggest that the class of such systems is not coextensive with the class of physical dynamical systems. While every physical notational scheme or system is a physical dynamical system, not every physical dynamical system, under the relevant analysis, is a notational scheme or system. Physical notational schemes and systems are a proper subset of physical dynamical systems.

What would it mean for the class of physical notational systems to be a subset of physical dynamical systems? I take it that what this means (at least in part) is that the physical/causal story one tells of some dynamical systems meets the PNS-constraints and that there are dynamical systems whose physical/causal story violates one or more of the PNS-constraints. So the question becomes, is there a fact of the matter as to whether a given dynamical system meets the constraints for a physical notational scheme or system? I will argue that in the case of notational schemes there is such a fact relative to an individuation of computational states. In the case of notational systems there is such a fact relative to an interpretation of the computational states. Such facts exist because both the individuation and interpretation of computational states is constrained by the physical/causal structure of the system.

Lets look at notational schemes first, and ask the question whether a particular dynamical system -- for example, the solar system -- is a physical notational scheme. If we accept the physical/causal story given by Newtonian mechanics -- which recognizes things like planets, gravitational force, the shape of orbits, etc. -- and use it to individuate the states and transformations of the systems (which are mapped onto computational states and transformations), our question becomes something like, "do the orbits of the planets around the sun constitute a notational scheme?". I think one can unproblematically say they do not. For one thing, the instantaneous descriptions of the system will be densely ordered and thus violate the effective differentiability constraints.

Of course, it is possible to take the solar system and individuate components and relations in such a way that the PNS-constraints on schemes are met. For example, a colleague suggested the following individuation: "we can divide up the orbit into quadrants, assign them numbers, think of them as states, and observe that each is followed by the next with law-like regularity."¹² While this is logically coherent, the point is that there is nothing in our physics (i.e. our science of the solar system) that requires, necessitates, or sanctions such an individuation. There are two reasons why such individuations are not generally sanctioned. First, they do not pick out higher level regularities which deepen our understanding of the system. (If they did pick out such regularities, we would incorporate them into our scientific story.) Second, they may not even coincide with our scientific story. For example, where a planet is located in a quadrant at time t_i does not matter for this particular individuation, but it may matter very much to the physical/causal story. It may be the case that particular locations in the quadrant are associated with varying degrees and types of causal interactions with other heavenly bodies. If this was the case, this individuation would not coincide with our physics and could be dismissed on that basis.

Let us ask the same question about digital state computers. In such systems voltage levels constitute states of the machine. The actual voltage levels are of course continuous and variable as depicted in Figure 4. It is also the case that each and every point and fluctuation of the current is (for some purpose or under some analysis) causally efficacious in the world. But every point and fluctuation is not causally efficacious in the operation of the system as a digital state computer.

--

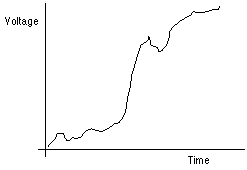The system is structured in such a way that a function such as in Figure 5 can be used to map the continuous, variable voltage levels onto a notational scheme with two elementary characters (0/1, true/false, on/off) by:¹³ (1) demarcating two ranges of voltages levels (character inscriptions) such that they are "perceptually" discernable to the relevant mechanical process; (2) setting up the system such that every voltage level within a range has identical causal consequences (i.e. is character indifferent); (3) making sure there is gap (discernable by the relevant mechanical process) between ranges which is not causally efficacious in the operation of the system (i.e. is not an inscription or character in the system).

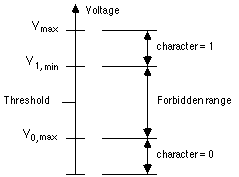
The result is a notational scheme such as graphed in Figure 6. It is Figure 6 rather than Figure 4 which gives the correct causal account of the dynamics of the system qua digital computer. This account both, captures interesting regularities which deepen our understanding of the system and coincides with the scientific/physical story of the system.

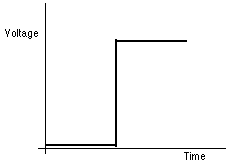
Can we make the same claims about physical notational systems? Given an arbitrary physical dynamical system, can there be a fact of the matter as to hether it is a physical notational system or not? If you choose not to interpret the system semantically, clearly there can be no such fact. The question would never arise. However, the important point is that, if you do choose to interpret the system, then relative to a specific individuation of states and transformations (as in the case of schemes) and a specific interpretation, there is a matter of fact as to whether the system is notational or not. To get this matter of fact, you proceed as follows:

(i) Decide on the system and phenomenon you are interested in and the level at which it occurs.

(ii) Understand the system/phenomenon on its own physical/causal terms; i.e. explicate the structure and dynamics of the system which are causally relevant in the production of the phenomenon under investigation.

(iii) Use the physical/causal structure to individuate equivalence classes of physical states and transformations which are to be assigned to computational states and transformations.

(iv) Specify the program the system is supposed to be running and again use the causal structre and dynamics of the system to interpret the computational states and transformations.

(v) Ask whether this individuation and interpretation meets the constraints on physical notational systems.

The system under investigation may or it may not meet the PNS-constraints. It may fail in the first instance because the causal structure and dynamics of the system results in an individuation of (computational) states and transformations which do not meet the constraints on notational schemes. It may fail in the second instance because -- since reference is correlated with causation -- the causal network of the system may not support the interpretation of computational states and transformations required by the program which the system is supposed to be running.

Is our stomach -- as a processor of food -- a physical notational system with respect to a certain individuation and interpretation of computational states and transformations? It is an empirical question. There is no a priori answer. One needs to proceed as above and discover the answer. Is our brain a physical notational system under some individuation and interpretation of computational states and transformations? Do the structure and dynamics of the brain which are causally relevant in the production of mental life satisfy the notationality constraints? Maybe they do; maybe they don't. It is, as cognitive science claims, an empirical question.

Since the facts about notationality are relative to an individuation and interpretation of computational states and transformations, they need not be a unique facts. A system may turn out to be a physical notational system with respect to several individuations and interpretations. But there is no reason to believe that it will turn out to be a notational system with respect to every individuation and interpretation because the notationality constraints tie the individuation and interpretation into the physical/causal structure of the system.

Note the important difference between this construal and the utility reply. The utility reply says that, given any physical dynamical system one can choose to describe it in either physical or information processing vocabulary. The phenomenon stays constant, only the description changes depending on which is more useful. On the account here, what I am suggesting is that before one has the option of switching vocabulary (i) the actual physical system and the individuation and interpretation of computational states and transformations have to meet certain stringent constraints; and (ii) by making the switch, the theorist is making a very strong empirical claim to the effect that those aspects of the structure and dynamics of the system captured by the six constraints on physical notational systems (PNS-constraints) are causally relevant in the production of the phenomenon under investigation.

Now if it is the case that notationality is a necessary condition on computational information processing, and that the class of physical notational systems is a small subset of the class of physical dynamical systems, then the claim of vacuousness of computational information processing is simply unwarranted. It is simply not the case that everything can be accurately described as doing computational information processing.

6.0 Physical Symbol Systems are Physical Notational Systems

The class of mechanisms we generally appeal to when talking about computational information processing -- on the classical account -- are physical symbol systems (Newell and Simon, 1981; Newell, 1980). In this section I will argue that physical symbol systems are indeed physical notational systems, and thus immune to the objections of vacuousness.

In a physical symbol systems the physical states of the machine correspond to marks or inscriptions and the computational states correspond to characters. A function (which Pylyshyn calls an instantiation function ) maps physical states on to computational states. The machine states are character-indifferent, disjoint equivalence-classes.

The mapping from the physical states to the computational states is determinate. That is, for any computational states, cs1 and cs2, and any single physical state, ps1, if ps1 does not genuinely belong to both cs1 and cs2, it is perceptually possible (for the relevant mechanical process) to determine either that ps1 does not belong to cs1 or ps1 does not belong to cs2.

The causal constraint is also met. Certain physical states in the instantaneous description at t_n have "the right kind of causal connection" to certain physical states in instantaneous descriptions at t_n-1 and t_n+1. The transformation of the computational state CS_n at t_n into CS_n+1 at t_n+1 is realized as the causal transformation of physical state PS_n at t_n into PS_n+1 at t_n+1, where PS_n at t_n and PS_n+1 at t_n+1 are a subset of physical states of the system which are to be mapped onto computational states.

The compliance link (computational pointer) in physical symbol systems is unambiguous, or so I claim. Every symbol has the same, single compliance-class in every instance, regardless of context. This however is not an uncontentious claim. Some prominent computer scientists (e.g. Smith, forthcoming) insist that computation is fraught with context-dependency and hence ambiguity. They point to the following types of phenomenon to substantiate their claims: (1) When a function F1 is called from inside another function F2, the two functions can use the same variables, but give them different referents. For example, in function F1 the variable DeviceJ might be initialized to printer1. In function F2, the variable DeviceJ might be reused but in this case be initialized to plotter3. So we would seem to have a case where at the same point in time we have the variable DeviceJ referring to either printer1 or plotter3. (2) When you type 'mail' to your Unix system, it retrieves the messages that are currently on the queue, specifically, m7, m8, & m9. But when you gave the command yesterday, it retrieved the messages that were there then, specifically, m3, & m4. So we would seem to have a case of the same symbol having different referents depending on temporal context.

Neither of these cases is however problematic. In the first case, the system is structured in such a way that it only has access to the variables associated with the function just called. The calling function is pushed lower onto the stack and momentarily inactivated. Thus there is no ambiguity. The second example is not a case of semantic ambiguity either, because all that the PNS-constraints required was unambiguity internal to each instantaneous description. This is all that is necessary because the interpreter evaluates the states at each instantaneous description. Past and future instantaneous descriptions are not considered. The mail example clearly reaches across instantaneous descriptions.

The membership of entities in compliance classes is effectively differentiable. Since the correlated objects are other states which have already passed the requirement of syntactic finite differentiation, semantic finite differentiation comes for free.

The transformation of the system from one instantaneous description to the next instantaneous description is such that the above five criteria are preserved.

Thus we see that physical symbol systems do indeed meet the six constraints on physical notational systems. Indeed, it is notationality that makes physical symbol systems possible. The syntactic criteria (PNS1 & PNS2) allow us to assign computational states to physical states and collapse the distinction between the two. This means that we can manipulate the computational states by manipulating the physical states of the machine. The semantic criteria of unambiguity ensures that syntactic equivalence will entail semantic equivalence. Collectively, the two semantic criteria (PNS4 & PNS5) ensure that the system can always be systematically interpreted. When these criteria are preserved in the dynamical evolution of the system (PNS6) we can interpret the intermediate steps. When the causal constraint is satisfied (PNS3) we can causally implicate the semantic content of the computational states in the explanation of behavior. It is by virtue of being physical notational systems that physical symbol systems satisfy the C'-constraints on computational information processing.

7.0 Cummins' Interpretational Semantics Requires a Notational Scheme

I have motivated and elaborated a story of computational information processing which is pretty standard in the literature and captures the intuitions and practices of many practitioners (Newell and Simon, 1972, 1981; Newell, 1980, 1987) and shown that the system that this story must appeal to, and indeed does appeal to, is a physical notational system. Cummins (1989) has a related notion of computational information processing, which is similar in some respects and different in others.¹⁴ The task of this section is to show that Cummins' construal requires a commitment to a subset of the notationality constraints.

Rather than talking in terms of information processing, Cummins prefers to talk about computing functions. On his account, the claim a certain cognitive capacity is a computational capacity is a claim that the cognitive capacity in question is a cognitive function from certain inputs to certain outputs and that the cognitive system computes this function. There are two obvious problems here. The first problem is simply, how does one individuate cognitive functions? The second problem is, what is it to compute a function? Cummins does not seem concerned about the first but does try to deal with the second.

Cummins distinguishes between function computation and function satisfaction. He recognizes that any physical system can satisfy functions (e.g. "set mouse traps satisfy a function from trippings to snappings without computing it" (Cummins, 1989, p.91)), but wants to argue that not any physical system can compute a function. Computing is to be explained as "program execution". Program execution reduces to "disciplined step satisfaction" (p. 92):

The obvious strategy is to exploit the idea that program execution involves steps, and to treat each elementary step as a function that the executing system simply satisfies. To execute a program is to satisfy the steps.

The steps must of course be satisfied in the right order, hence the need for the "discipline". But the discipline comes for free (p. 92):

Functions satisfied by d specify causal connections between events in d, so if d satisfies f and g and if the current value of f is an argument for g, then an execution of the f step will produce an execution of the g step.

He suggests thinking of program execution in the following way (p. 92):

Imagine the program expressed as a flow chart. Each box in the chart represents a step. To execute a step is to satisfy its characteristic function, i.e., the function specified by the input/output properties of the box. If you think of the arrows between the boxes as causal arrows, the result is a causal network with steps (i.e., functions to be satisfied) at the nodes. A system executes the program if that causal network gives the (or a) causal structure of the system.

What Cummins' account amounts to is that there is some function and some device and that certain states and state transformations of the device can be interpreted as the variables and logical transformations called for in the program which executes the function. While I believe there are some serious problems in talking about computing functions¹⁵ the picture that emerges here is not unlike the picture in Figure 3 in that there is an isomorphism between the states of the machine and the steps in some algorithm. But there is one important difference in the two stories. On Cummins' account there is no accompanying story of reference, either internal or external to the system. Thus the picture is actually more like the one in Figure 7.

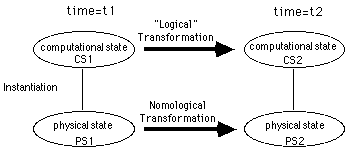
In articulating this story, Cummins however does not go far enough in specifying the constraints on such a system. What are some of the properties that a system must have if it is to be interpretable in this way? What is it that makes "disciplined step satisfaction" possible and allows us to distinguish function computation from function satisfaction?
I want to suggest that any system that qualifies as computing a function on Cummins' account will have to meet a subset of the PNS-constraints. In particular it must be a notational scheme and satisfy constraints PNS1, PNS2, PNS3 and PNS6'.

If the system fails PNS1 such that equivalence classes of physical states which are mapped onto computational states are not disjoint, there will be no fact of the matter as to which computational state some physical state instantiates. If there is no such fact then there can be no mapping of that physical state onto a computational state. If the system fails PNS2 such that it is not possible to determine which equivalence class a given physical state belongs to, then no procedure will be able to effectively make the assignment. If the system fails PNS3 then we will not get the "discipline" Cummins requires. If the system fails PNS6' then one or more of the above three constraints will be violated.

Notice that if Cummins was to incorporate a notion of reference in his story, then it would be identical to the physical symbol system story of computational information processing articulated in the previous sections and would then have to satisfy all six of the notationality constraints.

8.0 Fodor's LOT is Substantially a Physical Notational System

So far I have motivated physical notational systems on the grounds that they are necessary to satisfy the C'-constraints and give us a nonvacuous notion of computational information processing, and argued that physical symbol systems (and to a large extent Cummins' Interpretational Semantics) do indeed meet the notationality criteria. I now want to argue that even if you motivate the computational story, independently of this notion of computational information processing, as for example is done by Fodor and Pylyshyn (1988) in the Language of Thought (LOT) story, the underlying system that you are appealing to must still be substantially a physical notational system.

On the LOT account, what is absolutely essential about the "classical architecture" mechanism is its combinatorial syntax and semantics and "structure sensitive to process" (Fodor, 1987; Fodor and Pylyshyn, 1988). Combinatorial syntax and semantics and structure sensitivity to process are properties of computational systems (at least in classical architectures) which are also thought to be properties of LOT. The idea is that systems with these properties are interesting because they simultaneously satisfy the following constraints on cognitive systems, and they do so by virtue of their combinatorial syntax and semantics and structure sensitivity to process:

1) The Structure of Mental States: Fodor and Pylyshyn pick out four constraints that the structure of mental states must satisfy -- productivity, systematicity, compositionality and inferential coherence -- and argue only a system with a combinatorial syntax and semantics can meet these constraints, hence LOT must have a combinatorial syntax and semantics.

The productivity argument says that the generative/understanding capacity of the human cognitive system is unbounded -- but is achieved by finite mechanisms. One way of achieving this is with the recursive application of a finite set of rules to a finite set of primitive symbols which results in an unbounded set of expressions.

The systematicity argument is that the human cognitive system's ability to "produce/understand some sentences is intrinsically connected to the ability to produce/understand certain others" (Fodor and Pylyshyn, 1988, p. 23). That is, learning a language is not the same as memorizing lists of words or phrases. (If it was, then it would be possible to understand "John loves Mary" without understanding "Mary loves John".) If you have mastered a language there is a remarkable degree of systematicity in your ability to understand sentences in that language. Such systematicity is a mystery unless one assumes constituent structure.

The compositionality argument is related to systematicity. The argument is that "a word makes approximately the same semantic contribution to the meaning of every expression in which it occurs" (Fodor and Pylyshyn, 1988, p.27), thus the meaning of a complex expression is a function of the reference of the atomic symbols and the rules of composition of the language.

Finally, the inferential coherence argument requires that similar logical form be dealt with similar inference machinery, and entail similar consequences.

The claim in each case is that these are properties of mental states and are also properties exhibited by certain mechanisms by virtue of their combinatorial syntax and semantics, thus giving us reason to believe that the LOT also has a combinatorial syntax and semantics.¹⁶

2) Causal Efficacy of Semantic Content: This is a "what else could it be" argument advanced by Fodor on several occasions (Fodor, 1975, 1981, 1987). The claim is that the "structure sensitivity to process" property of LOT provides a solution to the problem of mental causation. In fact, Pylyshyn (1984) claims that the computational story is the only non-question begging account that we have for connecting the semantic and causal properties of symbols.

The computational "solution" to the problem of mental causation draws upon two important innovations: (i) the development of formal systems, and (ii) the mapping of formal systems onto mechanical/electronic circuitry. The significance of formal systems for our purpose is that symbols in such systems are purely syntactic structures. Their "content" is strictly a function of their syntax. Now, as is well known, in a formal system, given an interpretation of that system in which the axioms are true, the purely syntactic rules of inference will guarantee the truth of the theorems under the same interpretation. Thus the syntactic properties will preserve and propagate the semantic properties. When formal systems are realized in physical dynamical systems, the syntax is instantiated in the machine by virtue of some physical property (e.g. shape, size, etc.), and the operations of the machine can be made to be sensitive to this property. As such, the symbols can said to be causally efficacious in the world.

Now I want to show that notationality is a prerequisite for the LOT architecture that Fodor and Pylyshyn have in mind. Fodor and Pylyshyn focus on several crucial properties of LOT, namely:

* causal efficacy of computational states

* structure of computational states

* productivity

* systematicity

* compositionality

* inferential coherence

Furthermore, they claim that the only way we know how to achieve these properties is in a system which has a combinatorial syntax and semantics, and is structure sensitive to process (Fodor and Pylyshyn, 1988). The question then becomes, what is the relationship between the six PNS-constraints on physical notational systems and combinatorial syntax and semantics and structure sensitivity of process?

A combinatorial syntax requires a discrete alphabet. But without syntactic disjointness and finite differentiation (PNS1, PNS2) there can be no such alphabet, and without such an alphabet it would be senseless to talk about combinatorial syntax. But it is quite possible to have a disjoint and finitely differentiated alphabet without further committing oneself to a combinatorial syntax. Without a combinatorial syntax it is senseless to talk about a combinatorial semantics. But it is possible to have a combinatorial syntax without committing to a combinatorial semantics.

The structure sensitivity of process requires that (i) character-indifference be a function of some causally efficacious property of physical states (PNS1); (ii) equivalence classes of computational states be disjoint (PNS1); (iii) computational states be effectively differentiable (PNS2); (iv) the causal constraints as specified in PNS3 be met; and (v) the correlation of compliance-classes with computational states be unambiguous (PNS4). Finally, if the combinatorial syntax and semantics, and structure sensitivity of process are to be maintained, then each of the above constraints must be maintained (PNS6).¹⁷

Requirements (i), (ii), and (iii) permit the collapse of the distinction between physical states and computational states. If to this we add requirement (v) we get a guarantee that syntactic equivalence will entail semantic equivalence. If we further add requirement (iv) we will get an isomorphism between the computational states and physical states. Each of these is necessary for structure sensitivity of process.
So the conclusion would seem to be that physical notational systems constitute a necessary condition for LOT. But LOT only constitutes a sufficient condition for physical notational systems. It would seem that LOT is a physical notational system but not every physical notational system is a realization of LOT. (This same relationship holds between physical symbol systems and physical notational systems.)

Thus both LOT and physical symbol systems are physical notational systems, and by virtue of being physical notational systems qualify as computational information processing systems. But interestingly, they are not coextensive with physical notational systems. They are both subsets of the set of physical notational systems. This means that notationality is a much more basic commitment for us than physical symbol systems or LOT. It also means we can coherently be committed to some form of computational information processing without being committed to physical symbol systems and LOT. This has consequences for connectionism.

9.0 A Note on Connectionism: Information Processing Without Symbols

Thus far I have confined the discussion to the "classical" story and argued that what we are really committed to on this account are physical notational systems, and physical notational systems, while necessary for physical symbol systems and LOT are not coextensive with either. This leaves open the possibility of mechanisms which are not realizations of physical symbol systems or LOT but can none the less satisfy the C'-constraints on computational information processing. A question which comes to mind in the current context is whether connectionist networks are such systems? Or more generally, where does connectionism fit into this picture?

Unfortunately there is no straight forward answer to the question at this time. The problem is that, while connectionists make a commitment to the notion of information processing, they have failed to elucidate and ground their claims in any set of intuitions which do justice to the term (like the C'-constraints try to do for the "classical" story).

Furthermore, there is not one but several conceptually distinct research efforts being carried on under the general heading of connectionism. They can be categorized in terms of the source of their inspiration and theoretical vocabulary. There are three main sources: performance psychology,¹⁸ physics, and biology. The resultant corresponding categories of research are parallel distributed processing (PDP), physical dynamical systems modeling, and neuronal modeling.

Much of the work associated with the PDP Group is concerned with modeling some real-time performance aspects of cognition (e.g. Chap. 1 in Rumelhart and McClelland, 1986; Part IV in McClelland and Rumelhart, 1986). The models are viewed as architectural variants of physical symbol systems (hence information processing systems of some kind), and the basic game is to pick some performance properties of cognitive systems (e.g. typing, letter recognition, word recognition) and to show that the PDP architecture can accommodate the the task more accurately and naturally than the physical symbol systems architecture. Yet the participants are anxious to insist that they are not "merely" exploring different implementations of physical symbol systems but are making substantive theoretical claims, quite different from those associated with physical symbol systems (see for example the exchange between Broadbent (1985) and Rumelhart and McClelland (1985), and chapter 4 in Rumelhart and McClelland (1986)). To evaluate and do justice to this controversy would take us too far afield. So I merely note it and set it aside.

The physics inspired models (e.g. Smolensky, 1986, 1988; Tank and Hopfield 1987; Hinton and Sejnowski 1986) offer a more radical picture. On this account, the network (and the cognitive system) is viewed as a continuous physical dynamical system, evolving through time like any other physical dynamical system, and doing "subsymbolic" or "numerical" computations (Smolensky, 1988) rather than symbolic computations. There are a number of outstanding questions as to the cognitive significance of these models. But as some of these objections have been recently raised in Searle (1990) and Goel (1990) I will not repeat them here. What I do want to note about these researchers is that while they want to abandon the notion of symbol manipulation in favor of continuous numerical computations, they want to hang on to the notion of information processing.

This latter point must also be made in connection to the biologically or neurologically inspired models. While these researchers take neurology very seriously -- and despite their disparaging remarks about classical AI and connectionist networks which only "look sideways to biology" (Reeke and Edelman, 1988) -- they are also committed to the notion of information processing, albeit with slightly different computational architectures.

Thus the notion of information processing is a common theme running through each of these three endeavors. Yet each group claims that they are offering a different account from each other, and a radically different account from the computational information processing story associated with physical symbol systems and LOT, and that this difference is of considerable theoretical importance to cognitive science.

The difficulty in accessing these claims is in understanding what connectionists mean by information processing. It is not clear whether they would accept the C-constraints on cognitive information processing as interesting or relevant. It is very doubtful that they would accept the C'-constraints on computational information processing.

But in terms of our discussion, what is interesting to note is that it is not necessary (or even desirable) to satisfy the C'-constraints. Ideally what one wants to do is satisfy the C-constraints. This option is open to connectionists so long as they come up with an account of reference and content which is similar to that of human mental states. But I suspect this is just not in the cards in the foreseeable future.

If however, they want to stay with the current computational notions of reference and content, then there seem to be few nonvacuous alternatives to the C'-constraints. Without the ability to assign specific values to specific physical states and recover them (constraint C1') it is not clear how one could even get started on the road to information processing. And without constraint C2' one would have no basis for implicating representational content. One would just have a black box with a certain input and output and this strictly behavioral story would be subject to the charge of vacuousness.

There is evidence that at least some connectionists are trying to satisfy the C'-constraints. I take it that the enormous amount of effort currently being devoted to interpreting the hidden nodes in multi-layered networks is in effect an attempt to find an analysis under which the network is a physical notational system and satisfies the C'-constraints.

Another option for connectionists is to give up the notion of information processing all together. The difficulty here is in knowing what to replace it with. We simply don't have a clue as to what types of non-semantic predicates we could apply to processes that mediate between two representational states. It seems to me that the two options which hold the greatest promise of rapid transformation and advancement of the field are to motivate a notion of cognitive information processing independent of the C-constraints, or if one is going to accept the C-constraints, find a mapping from them onto a new set C'' which does not require a commitment to physical notational systems.

10.0 Conclusion

Given cognitive science's commitment to computational information processing (and LOT) it would seem that what cognitive science is really committed to are physical notational systems. That is, in appealing to computation, and claiming it is a necessary condition for cognition, we are claiming that the system which underwrites computational information processing (i.e. a physical notational system) is also necessary (but not sufficient) for cognitive information processing. This constitutes a substantive, nonvacuous claim about the structure of the cognitive system. It may of course be false, but that can only be determined by empirical inquiry.

It is worth noting that the appeal to notationality is not really an option for us. If I am correct about our commitment to the C-constraints, and the fact that we believe that we can, in part, satisfy them by satisfying the C'-constraints, then the appeal to notationality would seem to be logically implied. Be as it may, the account has a number of troubling consequences which have not been fully appreciated in the literature.

First, while the C-constraints account recognizes the semantic content of mental states at time t_i and t_j, and causally implicates that content in the evolution of the system from t_i to t_j, it does not entail that the mediating processes also be semantic. But the C'-constraints commit us (by virtue of constraint C2'(i)) not only to the semantic content (interpretability) of instantaneous descriptions at time t_i and t_j but also to the semantic content (interpretability) of the mediating instantaneous descriptions. We have experiential evidence of the semantic content of some mental states. But there is no corresponding evidence that the cognitive processes which mediate between such states are also representational. Hence we are forced to argue that these processes are unconscious. (But in all fairness, it should be noted we currently have little choice but to make the assumption that these processes are semantic, because as noted above, at the moment we can't even imagine what type of non-semantic predicate we could apply to a process which mediates between two semantic states.)
Second, it leaves cognitive science in the position of postulating a notational device to explain the human cognitive system's ability to process symbols. But given the fact that most of the symbol systems processed by the cognitive system (e.g. natural language, pictures, diagrams, etc.) are not notational systems, it is a rather odd conclusion at best. It is of course possible to argue that transducers map external non-notational symbol systems onto a notational internal symbol system but this is implausible (see Goel, 1991).

Third, we must claim that notationality is a necessary condition on cognitive systems. This of course doesn't mean that one has to equate mental phenomenon with notationality, but it does mean that there can be no minds without notationality. This seems implausible on both logical and empirical grounds.

Fourth, there is nothing in the C-constraints which requires a stronger relationship than supervenience between the physical and mental states. Supervenience is however not sufficient to satisfy the C'-constraints. As we have seen, a much stronger relationship is required. This seems to violate some rather strongly held intuitions. Incidentally, it also suggests that computational functionalism -- the doctrine that computational states can be realized in any physical system -- is not as coherent a story as widely thought.

Fifth, this account would suggest that cognitive science can not proceed independently of neurophysiology. It will be necessary to do the neurophysiology before the major claim of cognitive science -- that the brain is (in part) a computational information processing system -- can be verified or falsified.

Finally, perhaps the most troubling difficultly is the following: We end up appealing to a notational system to explain the cognitive system's ability to process information. But the reason we needed a notational system to begin with was that we were satisfied with a computational account of content and reference which is substantially different from that of human mental states. The difficulty of course is that, from the fact that we need notationality to satisfy the C'-constraints, nothing logically follows about the C-constraints.

The dilemma we are confronted with is that while a pre-notational account of computational information processing is vacuous, a notational account distorts the subject matter. By settling for a computational account of reference and content, cognitive science has in effect reduced the science of the mental to the enterprise of mapping non-notational symbol systems onto notational systems. While this is a potentially interesting field of study, it is not clear what it has to do with human cognition.

Where does this leave us? I think we have at least four options. (1) We can give up talking about semantic notions and information processing and try to give a strictly physical account of the mental. (2) We can take the notions of content and reference as they occur in the case of human mental states seriously, accept that we can't say anything about them in computational terms and try to develop a non-computational, biological account. (3) We can, as noted above, try to motivate a notion of cognitive information processing which is independent of the C-constraints. (4) We can try to reconstruct the notion of computation in such a way that the resulting notions of content and reference do justice to the human case and satisfy the C-constraints.

The first of these is implausible. It is shamelessly reductive and denies the existence of the very phenomenon that is to be the object of study. The second is the one which has been urged by Searle (1984) for many years. If we can carry it out we win on all accounts: we get a physically realized notion of information processing without notationality. But it is not clear what type of enterprise this would be. It certainly would not be cognitive science in the present sense of the word. The third is being undertaken by Cussins (1990) in his development of the notion of non-conceptual content. If successful it will have an important impact on the field. The fourth is Smith's (forthcoming) intellectual enterprise. If successful it would allow us to tell a coherent, non-vacuous story about computational information processing without leaning so heavily on notationality. I think it will require such a story to ultimately vindicate cognitive science.

References

Broadbent, D. (1985), 'A Question of Levels: Comment on McClelland and Rumelhart', Journal of Experimental Psychology, General, vol. 114, no. 2, pp.189-192.
Chomsky, N. (1965), Aspects of the Theory of Syntax, Cambridge, MA: MIT Press.

Chomsky, N. (1980), 'Rules and Representations', .Behavioral and Brain Sciences, Vol. 3, pp. 1-61.

Churchland, P. S. (1986), Neurophilosophy, Cambridge, MA: MIT Press.

Cummins, R. (1989), Meaning and Mental Representation, Cambridge, MA: MIT Press.

Cussins, A. (1990), ''The Connectionist Construction of Concepts', in M. A. Boden, ed., The Philosophy of Artificial Intelligence, Oxford: Oxford University Press.
Dennett, D.(1987), The Intentional Stance, Cambridge, MA: MIT Press.

Dretske, F. 1989. 'Putting Information to Work', in P. P. Hanson, ed., Vancouver Studies in Cognitive Science, Vancouver, Canada: University of British Columbia Press.

Elgin, C. Z. (1983), With Reference to Reference, Indianapolis, Indiana: Hackett Publishing Co.

Fodor, J. A. (1981), 'The Mind-Body Problem,' Scientific American, vol. 244, no. 1, pp.114-123.

Fodor, J A. (1981), 'Methodological Solipsism Considered as a Research Strategy in Cognitive Psychology,' in J. Haugeland, ed., Mind Design, Cambridge, MA: MIT Press.

Fodor, J. A. (1987), Psychosemantics: The Problem of Meaning in the Philosophy of Mind, Cambridge, MA: MIT Press.

Fodor, J. A. and Pylyshyn, Z. W. (1988), 'Connectionism and Cognitive Architecture: A Critical Analysis', Cognition, vol.28, pp.3-71.

Goel, V. (1990), 'Smolensky's PTC: Having it Both Ways', The Behavioral and Brain Sciences, vol. 13, no. 2, pp. 400-401.

Goel, V. (1990), 'Specifying and Classifying Representational Systems: A Critique and Proposal for Cognitive Science', manuscript submitted for publication.

Goel, V. (1991), 'Sketches of Thought: An Empirical and Logical Investigation into the Role of Sketching in Design Problem Solving', Ph.D. Dissertation, UC-Berkeley.

Goodman, N. (1976), Languages of Art: An Approach to a Theory of Symbols (Second Edition), Indianapolis, Indiana: Hackett Publishing Co.

Hamacher, V. C., Vranesic, Z. G., and Zaky, S. G. 1978, Computer Organization, NY: McGraw-Hill.

Haugeland, J. (1978), 'Nature and Plausibility of Cognitivism', The Behavioral and Brain Sciences, vol. 1, pp.215-226.

Haugeland, J. (1984), Artificial Intelligence: The Very Idea, Cambridge, MA: MIT Press.

Hinton, G. E. and Sejnowski, T. J. (1986), 'Learning and Relearning in Boltzmann Machines,' in D. E. Rumelhart, J. L. McClelland and the PDP Research Group, eds., Parallel Distributed Processing, Vol. 1: Foundations Cambridge, MA: MIT Press.

Johnson-Laird, P. N. (1983), Mental Models, Cambridge, MA: Harvard University Press.

Kohlers, P. A. and Smythe, W. E. (1984), 'Symbol Manipulation: Alternatives to the Computational View of Mind', Journal of Verbal Learning and Verbal Behavior, Vol. 23, pp. 289-314.

Marr, D. (1979), 'Representing and Computing Visual Information', in P. H. Winston and R. H. Brown, eds., Artificial Intelligence: An MIT Perspective, Volume 2, Cambridge, MA: MIT Press.

McClelland, J. L., Rumelhart, D. E., and Hinton, G. E. (1986), 'The Appeal of Parallel Distributed Processing', in D. E. Rumelhart, J. L. McClelland and the PDP Research Group, eds., Parallel Distributed Processing, Vol. 1: Foundations, Cambridge, MA: MIT Press.

McGinn, C. (1989), Mental Content, Oxford: Basil Blackwell.

Miller, G. (1963), Psychology: The Science of Mental Life, N.Y.: Harper and Row.

Newell, A. (1980), 'Physical Symbol Systems,' Cognitive Science, vol. 4, pp. 135-183.

Newell, A. (1982), 'The Knowledge Level,' Artificial Intelligence, vol. 18, pp. 87-127.

Newell, A. (1986), 'The Symbol Level and Knowledge Level,' in Z. W. Pylyshyn and W. Demopoulos, eds., Meaning and Cognitive Structure: Issues in the Computational Theory of Mind, Norwood, NJ: Ablex Publishing.

Newell, A. (1987), 'Foundations of Cognitive Systems,' William James Lectures, Harvard University.

Newell, A. and Simon, H. A. (1972), Human Problem Solving, Englewood Cliffs, NJ: Prentice-Hall.

Newell, A. and Simon, H. A. (1981), 'Computer Science as Empirical Inquiry: Symbols and Search', in J. Haugeland, ed., Mind Design, Cambridge, MA: MIT Press.

Pylyshyn, Z. W. (1984), Computation and Cognition: Toward a Foundation for Cognitive Science, Cambridge, MA: MIT Press.

Reeke, G. N., Jr. and Edelman, G. M. (1988), 'Real Brains and Artificial Intelligence', Daedalus, vol. 117, no. 1.

Rumelhart, D. E. and McClelland, J. L. (1985), 'Levels Indeed! A Response to Broadbent,' Journal of Experimental Psychology, General, vol. 114, no. 2, pp.193-197.

Rumelhart, D. E. and McClelland, J. L. (1986), 'PDP Models and General Issues in Cognitive Science,' in D. E. Rumelhart, J. L. McClelland and the PDP Research Group, eds., Parallel Distributed Processing, Vol. 1: Foundations, Cambridge, MA: MIT Press.

Searle, J. R. (1980), 'Minds, Brains and Programs,' The Behavioral and Brain Sciences, vol. 3, pp. 417-457.

Searle, J. R. (1983), Intentionality: An Essay in the Philosophy of Mind. Cambridge: Cambridge University Press.

Searle, J. R. (1984), Minds, Brains and Science, Cambridge, MA: Harvard University Press.

Searle, J. R. (1990), 'Models and Reality', The Behavioral and Brain Sciences, vol. 13, no. 2, p. 399.

Skinner, B. F. (1953), Science and Human Behavior, N.Y.: Macmillan.

Smith, B. C. (forthcoming), Is Computation Formal?, Cambridge, MA: MIT Press.

Smolensky, P. (1986), 'Information Processing in Dynamical Systems: Foundations of Harmony Theory,' in D. E. Rumelhart, J. L. McClelland and the PDP Research Group, eds., Parallel Distributed Processing, Vol. 1: Foundations, Cambridge, MA: MIT Press.

Smolensky, P. (1988), 'On the Proper Treatment of Connectionism,' The Behavioral and Brain Sciences, vol. 11, no. 1, pp.1-74.

Tank, D. W. and Hopfield, J. J. (1987, December), Collective Computation in Neuronlike Circuits', Scientific American, vol. 257, no. 6, pp. 104-114.

Wegner, Peter. (1968), 'Programming Languages, Information Structures, and Machine Organization, N.Y.: McGraw-Hill.

Author Notes:

I am indebted to John R. Searle and Brian C. Smith for both inspiration and criticism in the writing of this paper. I worry that neither fully agrees with its contents. I take some comfort in the fact that there is no agreement between them as to where it is flawed. I am also indebted to Susan Newman for not being satisfied with an earlier version of this paper and insisting that I rewrite it and to Ken Olson and David Levy for many hours of Goodman exegesis. I would also like to thank two unanimous reviewers and the editor of this journal for helpful comments which improved the paper. This work is based on a chapter of the author's forthcoming dissertation (UC-Berkeley) and has been supported by a Canada Mortgage and Housing Corp. Scholarship, a Gale Fellowship, and a research internship at the System Sciences Lab at Xerox PARC. Correspondence and requests for reprints may be directed to the author at the Institute of Cognitive Studies (Bldg T4), University of California, Berkeley, CA, 94720.

End Notes:

¹ The first three are noted by McGinn (1989).
² It is however worth noting that there is nothing about these constraints that necessitates an appeal to computation. They are for example satisfied by a theory of mind such as Searle (1983).
³ This is perhaps also the most dangerous position to hold. It leaves one in the position of using computational vocabulary (e.g. "information", memory", "search", etc.) in one's theory of cognition without any explicit understanding of what the terms mean.
⁴ Two other answers to this question are discussed in sections 7.0 and 8.0.
⁵ I borrow this particular terminology from Elgin (1983).
⁶ The terms "correlation" and "compliance" are borrowed from Goodman (1976). Instead of talking about denotation or reference, Goodman prefers to talk in terms of the correlation or compliance of a symbol scheme with a field of reference. 'Correlation' is meant to be a little more broadly construed than 'denotation' so that words can be said to be correlated with their pronunciations and well as what they apply to or name in the world. Little hangs on the distinction for our purposes. I adapt the terminology to maintain consistency with later sections where Goodman's theory of notationality will be introduced.
⁷ Computation is first and foremost a process, that is, a sequence of time-ordered states, consisting on an initial state, intermediate states, and a final state. Each state in the sequence is often called an instantaneous description (Wegner, 1968). Each instantaneous description has several levels of descriptions and/or realizations, starting from the hardware level and ascending to various virtual machine levels. At the hardware level -- which is the level I am mostly concerned about -- they minimally consist of the contents of memory locations and various CPU registers, including the instruction register, the program counter register, memory address register, memory data register, and various general-purpose registers.
8 To simplify the exposition I will assume that reference, in so far as it is "explained" by computational systems, is restricted to other computational states and hard-wired devices. This is justified on the grounds that no one has developed a coherent version of the external reference story for computational systems. If and when such a story is developed, to the extent that it would be an extension of the internal reference story, my remarks can be extended to include it.
⁹ I believe that Chomsky's vocabulary of "cognizing" and "rule following" maps on to the notion of computational information processing in a straight forward way.
¹⁰ An exception to this is of course Project Zero at Harvard which was founded to explore the psychological implications of Goodman's theory. But to my knowledge they have not considered this particular application of Goodman's work. Other relevant exceptions are Haugeland (1978) and Kohlers and Smythe (1984).
¹¹ The dual of ambiguity is redundancy. It occurs where several inscriptions (which are not true copies of each other) have the same compliance-class. It is generally considered harmless.
¹² Kirk Ludwig
¹³ There are actually devices built into the system whose function is to sustain this mapping.
¹⁴ I am indebted to an unanimous reviewer for bringing Cummins' work to my attention.
15 It is simply too abstract a notion for our purposes. It propagates a harmful distinction between the notion of computation and the physical environment in which it is realized. While such Platonic conceptions maybe appropriate for mathematics, they are clearly not appropriate for cognitive science. It is just such characterizations which lead to the vacuousness objection. We need a theory which will allow us to talk about computation as a set of processes embedded in the physical world (see Smith, forthcoming).
¹⁶ Whether these are indeed properties of mental states is an open and disputed empirical question. But its empirical status is irrelevant for our purposes.
¹⁷ Fodor and Pylyshyn do not say enough about the semantic domain to determine if semantic finite differentiation (PNS5) is also required.
¹⁸ As opposed to competence psychology. The competence/performance distinction is of course due to Chomsky (1965).