Active and Passive Control of Structures
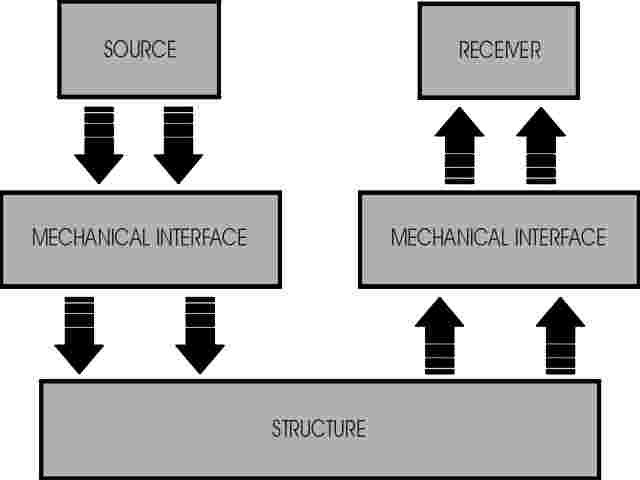
Low amplitude vibrations at frequencies between 1 and 1000 Hz, generally referred as microvibrations, have been neglected in the past due to the low level of disturbances induced on board satellites. In recent years however, microvibrations have been receiving growing interest in order to meet the increasingly restrictive stability requirements of satellite based instruments. These vibrations are produced by the functioning of on board equipment (sources) such as reaction wheels, gyroscopes, thrusters, electric motors, pumps, switches and all types of mechanisms, which propagate through the satellite structure towards sensitive equipment (receivers) such as microgravity experiments, or accurately targeted optical instruments, jeopardising their correct functioning.
To investigate strategies to reduce these dynamic disturbances by means of active control systems, realistic yet simple structural models are necessary to simulate the dynamics of the electromechanical system and compare the performance of possible control schemes. These models ought to include only the bare essentials in their representation of the physical system, meaning that they should include all the necessary elements to produce an accurate simulation of the dynamics of the system, without including unessential structural details.
These conflicting requirements, simplicity and realism, are merged in the modelling technique utilised in this work. Attention is focused on a mass loaded panel, which represent a typical satellite element, subjected to point excitation sources, the objective being to minimise the displacement at an arbitrary output location. Sensors and actuators for the active control system are twin patches of piezoelectric material bonded on the opposite faces of the panel.
Initial strudies have been carried out deriving the equations of motion by using Lagrange's equation with vibration mode shapes as the Ritz functions. The number of sensors/actuators and their location is variable. The set of equations obtained is then transformed into state variables and some initial controller design studies are undertaken. These are based on feedback control implemented by using full state feedback and an observer which reconstructs the state vector from the available sensor signal. Other control strategies,such as LQG/LTR, are presently beeing investigated, with particular attention to the robustness of the control system.
Other areas of further work include criteria for positioning the actuators and sensors, and upgrade of the structural model for a more accurate simulation of the dynamics of a real satellite structure.