The following terms are defined more fully later in the text, but are presented together here for ease of reference (see also FIGURE 1).

K: Hayden's definition (above) refers to K as an "ability of the environment" - a measure of resources. Carrying capacity has also been defined as the maximum population density theoretically supportable by the habitat (e.g., Hardesty 1977 p. 286; Ricklefs 1973 p. 783). Although the second definition appears to be more commonly used, its acceptance rests on a faith that resource availability is directly limiting the population - K is real and this is how one measures it. Because anthropologists do not neccesarily grant the relevance of K to humans, in this paper K will refer to an attribute of the environment. However, for simplicity's sake I will talk about populations "above" or "below" K as shorthand for "above/below the density supportable by K".

L [lambda] : K is determined by environmental minima (famines etc.), not maximal resource abundances. The most severe minima may occur once in thousands of years; these minima presumably do not determine K. K is set by less severe minima that occur more frequently. The measure of how frequently they occur is L (lambda), the interval between those minima which are determining K.

L_min: The shortest possible interval between biologically separate minima. "Minima" at shorter intervals act on the population as one long, continuous event.

L_max: The longest possible interval between minima which determine K. At longer intervals, each minima is "perceived" by the population as a unique event; there can be no adaptation to it.

In their extensive review of primate diets, Gaulin and Konner (1977) examine the common assumption that nonindustrial societies are living below K and conclude that
"nonindustrial economies are underproducing, maintaining lower than necessary levels of population density, and producing adequate calories and a surplus of protein and leisure most of the time. This is because of the periodically occuring shortages to which they are adapted." (p. 56, original emphasis)

The same emphasis on periodic shortages or catastrophes has been applied to arboreal frugivorous and folivorous primates by Cant (1980). He proposes that "During the crunch ... slower reproducers will be at a selective advantage because they are able to exist longer on fat reserves than are faster reproducers" (p. 542). Periodic shortages would thus strongly affect the evolution of reproductive rates in these animals. As pointed out by Southwood (1977), these alternations between favorable and unfavorable periods can have profoundly different consequences for different species, depending on the relation between generation time and the length of the periods. Species with short generation times track fluctuations of a given length more closely than those with longer generations; unfavorable periods lasting longer than a generation will cause local extinction. Southwood defines "favorable" and "unfavorable" as "allowing breeding" and "not allowing breeding" respectively, and is more concerned with population persistence/extinction than with the effects of less severe fluctuations (favoring/reducing breeding) on more subtle parameters. The most important of these is that of population density regulation, and many other biologists have focused on the importance of cyclic "crunches" for determining density (Slobodkin and Rapoport 1974, Wiens 1977). Anthropologists have been quick to see the implications of these theoretical treatments for understanding human ecology (reviews by Vayda and McCay 1975, Winterhalder 1980). It is generally recognized that very short cycles will elicit behavioral responses while long ones may cause genetic adaptation (Wiens 1977; "within generations" and "long time intervals" respectively), and further that very long intervals [e.g., 500 x (generation length), Slobodkin and Rapoport 1974] will cause the crunches to be perceived as "novel", each a unique event. There is a general feeling among biologists that cycles shorter than one generation will have effects qualitatively different from those of cycles longer than a generation (Winterhalder 1980); this appears to be a reasonable, but arbitrary, guesstimate. On the face of it, it seems even more arbitrary when applied to culture-bearing hominids (Winterhalder 1980).

Liebig's Law of the Minimum is not new, and pointing out the importance of minima alone has failed to rescue the K concept:
"If, indeed, the leanest season is really the limiting factor, then why not the leanest year of the decade, or why not the leanest year in a generation, or a century, or a millenium ? And which of these 'leanest' years should one take as a basis for estimating carrying capacity ? ... The carrying capacity measure degenerates into hopeless chaos." (Hayden 1975, p. 12)

To rescue K from this chaos, we must arrive at some non-arbitrary agreement regarding which leanest season is the minimum that determines carrying capacity. For humans, "minima" at 24 hour intervals (foraging at night being difficult) are not important; intervals of thousands of years render each crunch unique. Our goal is to determine L :
The length of the biologically relevant interval between minima, where minima are defined as brief (1) periods in which starvation is a major cause of mortality in the social group (see FIGURE 1). This need not mean that mortality is especially high or that the population experiences a genetic 'bottleneck'. Mortality is simply higher than average and much of it is directly attributable to resource scarcity.

Gaulin and Konner (1977) cite intervals of 1 - 15 years between such minima for a variety of human societies, but this finding is hard to evaluate: societies in which famine-level starvation is chronic are presumably not demographically stable, and are temporarily above K. Discussing monkeys, Cant (1980) states that "most of the time, perhaps for several months or even years at a stretch, resources are superabundant". Ripley (1980) is the first author I am aware of to attempt to link L to specific traits of the organism in question. In her discussion of seasonal cycles affecting grey langur monkeys, she concludes that "prenatal forms of population control" - presumably extended interbirth intervals - cannot be selected for if the interval between minima is greater than the "reproductive cycle", defined by her as (estrous + gestation). Although this attempt to link environmental and reproductive cycles calls attention to the need for a way of approximating L , I will argue below that Ripley's choice of (estrous + gestation) as the critical interval length is an underestimate of L. A female in a population near K who annually loses her unweaned infant will be under strong pressure to take time off from reproduction to increase metabolic reserves, if this will help her successfully rear her next offspring.

This difficulty with L can be overcome by applying natural selection theory, with its emphasis on the fitness (both classical and inclusive) of individuals (see Hamilton 1964). An individual, Ego, theoretically should behave so as to maximize her/his fitness, either by investing in close relatives or more directly in Ego's own offspring. "Investment" is used here in the sense of Trivers' 1972 definition of parental investment (PI) (2), but includes investment in non-offspring kin. Because this investment is by definition limited, during a good period it is wasteful to invest heavily in someone who derives low marginal utility from that investment; Ego should invest in additional relatives (e.g., have another child) (but see Barkow and Burley 1980 for post-demographic transition societies). During a bad period (a minimum) it would be in Ego's best interests to avoid investment in relatives (especially costly offspring) who die before they themselves have reproduced (Hayden 1972). On the other hand, the premature death of a relative in whom Ego has had no opportunity to invest directly represents only a small net cost (wasted investment) to Ego, via the cost to relatives in whom Ego did invest - e.g., the neonatal death of Ego's grandchild, born after Ego's own death.

The pattern and utility of investment thus gives us a basis from which to estimate L: intervals shorter than that necessary to produce an independant offspring will greatly constrain Ego's reproductive tactics, while intervals longer than an average lifespan will only indirectly affect Ego's behaviour. Plotted against interval length (FIGURE 2), the importance of K to Ego therefore is expected to follow a roughly sigmoidal curve. In a deterministic world, morbidity and mortality would be highly selective (i.e., nonrandom) and even small indirect effects of Ego's original investment might be significant (e.g., benefits to the health of a great-grandchild based on Ego's intensive investment in that individual's grandparent; see Hartung 1976). The effect of this selective mortality will be to give Ego an alternative strategy(s), making L longer; this is especially true if K-type strategies have evolved to minimize extinction probabilities (P. Ellison, personal comm.). L_max could, in theory, thus be extremely large, perhaps on the order of centuries for humans. The more common situation, however, is probably that of substantial randomness; under these conditions, for species exhibiting investment that may extend well into a relative's adult life (e.g., chimpanzees; Riss and Goodall 1977) L_max is likely to be roughly equal to the average lifespan.

Any interval less than L_max may have an effect on Ego's life history tactics (as defined by Stearns 1976), and that effect will be more pronounced as L is made shorter up to a point. This point (L_min in Fig. 2) is determined by the age at which offspring are able to repay investment in them, either by investing in (usually younger) sibs or by having offspring of their own. If L is less than this age, any attempt by Ego to split investment among several relatives entails a real and present risk to all of them, in proportion to their dependance on Ego. Insofar as Ego can predict such risks, s/he will disregard them at some (natural selection) cost. Changes in L below this value will have little effect on Ego's strategy or on K for that habitat, unless L becomes shorter than the physiological recovery period (leading inevitably to population decline).

It is important to emphasize that other factors besides resource availability may be affecting population numbers (e.g., predation, warfare), and that such factors may be more important to the individual than is K at any interval length. The effect of these other factors is represented by a dotted line in Figure 2. The value of the Y intercept (the importance of these phenomena) may take any nonnegative value. L for the population considered is then determined by the intersection of this line with the appropriate curve (if there is no intersection, K has no effect on the population).

The predictability of minima is based on L's variance (V). If this is small (minima come at regular intervals) Ego will probably be able to predict them on the basis of personal experience or explicit acquired knowledge (for humans); as V increases, these explicit predictions are less useful and "predictions" based on past genetic or cultural selection for different life history tactics will be more important. Note that cultural selection (cf. Durham 1976) can track environmental fluctuations of periods on the order of several thousand years (e.g., ice ages) much more efficiently than can genetical selection, and so for humans this past selection will almost certainly be cultural and not genetic in nature (3).

Emphasizing the cultural determinants of human population sizes, Cohen (1977) rejects the application of the K concept to humans:
"Human groups rarely exploit all the resources available to them. Actual consumption is determined by cultural choices, which in turn are based on a variety of factors: food preferences, nutritional needs, prestige, labor costs, and activity preferences. Thus population pressure need not take the form of exhausting resources or approaching 'carrying capacity'." (p. 49)

Plainly, nutritional needs and labor costs are factors that support the idea of a population regulated by K, but it is indeed hard to see how prestige and activity preferences could be considered aspects of K, biologically limiting local population density.

Werner et al. (1979) have reviewed the "lazy natives" arguement, and conclude that while cultural or "personality" traits may affect work effort, economic constraints are likely to be of primary importance. It is important to note that the South American Indian groups they base this conclusion on are all "undergoing rapid change", and to differentiate between (1) relatively "uncorrupted" cultures which value leisure time, and (2) cultures which have adopted Western faith in expansion and what are in effect technological means of increasing K faster than population size; both may be living at densities apparently below K. People in the second group may or may not have real economic opportunities to act on this faith and they will behave accordingly, as Werner et al. demonstrate. Only the first group is considered in this paper.

For example: Lee (1968) believes that the !Kung San of the Kalahari live well below the carrying capacity of their environment, based on the measured abundance of potential vegetable foods. Blurton Jones and Sibly (1978) have analyzed a variety of behavioral, physiological and ecological data in an attempt to determine whether or not the !Kung really are doing as well as they possibly can (i.e., living close to or at K). Their findings strongly and quantitatively support the idea that gatherer/hunter birth intervals are constrained by women's inability to carry more than one infant for long distances or with heavy loads such as mongongo nuts, a seasonal staple of the !Kung (see Lee 1980 and references therein).

As acknowledged by the authors, though, this finding does not represent a final answer to the question "What determines !Kung population density ?" They demonstrate that !Kung women cannot physically carry enough nuts to support their dependents during the two dryest months at any interbirth interval less than the observed four years. This may explain how the existing culture is limited, but it does not explain how the !Kung per se are limited -- why don't men and adolescents help gather ? Among the !Kung, not only the men but the very women whose labor might otherwise be eased prefer that men hunt (I. DeVore, personal comm.), even though the hunters are frequently unsuccessful. Children who seem old enough to work (to more than 16 years) generally do not (Draper 1976). It is possible that there are direct energetic and/or nutritional constraints operating (Wilmsen 1979); for example, inexperienced adolescents might waste more energy than they would acquire, and animal protein may be far more limiting than calories and plant protein, thus justifying calorically inefficient division of labor.

I would, however, suggest an alternative -- that inefficiency has been culturally "selected for" as a means of artificially limiting the population during good years to levels consistent with occasional and infrequent minima. In his review of atoll demography and K, Bayliss-Smith (1974) discusses the importance of food choice relative to food abundance and finds that
"... the perceived quality of a given diet rather than its actual nutritional adequacy will be the crucial variable that determines its acceptability. Except when some environmental catastrophe disrupted the system, it is therefore not likely that the theoretical limits of the carrying capacities of the North-Central Outlier atolls were ever reached." (pp. 275-6)

Under these conditions, K was reached; measurements of resource abundance under optimal conditions tell the ecologist how much is available under optimal conditions, and nothing more. Culturally-defined "good" diets limited populations to levels consistent with the diet available during a catastrophe. These observed cultural definitions of diet quality are based on cultural selection for dietary "inefficiency" that keeps the population in line with K (4).. Essentially the same suggestion has been made by Hayden (1972) who argues that incorporation of nonproducing individuals (e.g., religious experts, students) and activities (e.g., ceremonies, graduate schools) into society limits the group's ability to overexploit available resources. He considers this a means by which the population is limited to some comfortable density well below K. However, I believe this constellation of traits - nonproducers, "arbitrary" preferences for diets or leisure, nonproductive activity - is better viewed as a system of cultural adaptation to K, recognizing that K is determined by minima and not maxima (see also Just, 1980, for a similar model phrased in purely economic terms).

If leisure time is valued because "laziness" prevents population growth above K, emphasis on cyclic phenomena may shed light on the difference between "time-minimizing" and "energy-maximizing" cultures or even species (these categories were developed by Schoener (1971) and their application to humans reviewed by Smith (1979)). In the absence of extensive food storage or material inheritance, there is a limit to the usefulness of acquired energy (to be invested in kin or one's self) during a favorable period, and so energy maximization is pointless --until the crunch. This energetically favorable period may be used to prepare for some other sort of trouble, in which case the people may adopt an efficient time-minimizer strategy (Smith 1979) but it should be kept in mind that under certain conditions (no non-energy constraints, or no way to deal with them) people will essentially be "marking time". This may be done with a great deal of flair and imagination (storytelling, dance, perhaps ceremonies) and the activity may be regarded as central and important to the culture, but if the unconscious aim is to prevent the exploitation of temporarily abundant resources, it will be a mistake to argue that it is a part of an energy-efficient strategy. Contrary to Smith (1979) it is not always an advantage to be energy-efficient.

For humans, approximate values of L_max and L_min are 50 and 5 years, respectively. There are few data with which to place L within this theoretically determined interval. Gaulin and Konner (1977) found crunches at intervals of up to 15 years and Bayliss-Smith (1974) believes that hurricanes at roughly 20 year intervals directly limit Tikopian populations (though, he argues, intervals of approximately 50 years do not have such effects). Wilson (1981) examined the impact of lean years caused by El Nino on the coast of Peru, and argues convincingly that human populations there were regulated by crunches at 6 to over 20 year intervals (with a mean of about 13 years). These estimates of critical interval length correspond broadly to the age of social and sexual maturity in most human societies, suggesting investment in adult, socially independant relatives is generally outweighed by stochastic events and therefore that L is typically determined by the duration of intensive parental investment. This result should be generalizable to other animals as well. However, the major point being made here is simply that any interval less than L_max may have an effect on Ego's patterns of investment. Deviations of nonindustrial populations from Ks calculated on the basis of shorter periods must be interpreted carefully, and do not indicate the irrelevance of K to human population regulation.

Throughout most of human history, the "biological" K of the environment, determined by minima falling at intervals shorter than about 50 years, would thus have caused the (primarily or exclusively cultural) evolution of proximall "cultural Ks": density limits based on culturally regulated inefficiency of resource exploitation. Technological innovations (e..g., fire, stone points) may provide mechanisms for overcoming some minima and hence increasing the biological K; to the degree that specific technological changes are accepted more quickly than are general cultural overhauls (cf. Broom et al. 1967), this will result in a lag period during which the culture is truly living below K. As long as effective minima occur at intervals shorter than L_max, the culture will track the new biological K and eventually arrive at new cultural traits that establish a cultural K set by the new minima. Agriculture and food storage, especially of grains, may initially have provided a means of overcoming most minima, resulting in intervals longer than L_max; cultural selection could no longer create limits to growth and the pattern would become one of unrestrained growth punctuated by severe famines at intervals of greater than L_max years.

I would like to thank John Cant, Peter Ellison, Rick Potts, Jim Perry, and Barb Smuts for comments and several key references, and Irven DeVore and Mel Konner for the seminar that started this.

FOOTNOTES

(1) Brief relative to the lifespan of the animal; for most primates, less than one year. return

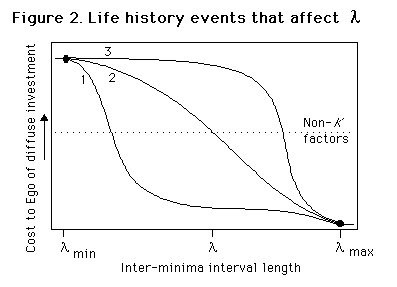
(2) "...any investment by the parent in an individual offspring that increases the offspring's chance of surviving (and hence reproductive success) at the cost of the parent's ability to invest in other offspring." (Trivers 1972, p. 139).return

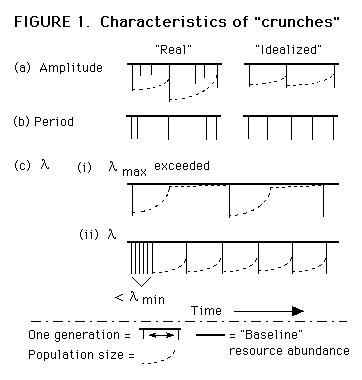
3 If V(L) is great relative to L and L is longer than a few years, it may become impossible to "plan" for minima by either method. As V(L) increases, however, the biologically relevant parameter will eventually become a function of the average interval between clusters of minima. return

4 Many atoll peoples also make very explicit attempts to control their own fertility and are fully conscious of K (Bayliss-Smith 1974); conscious and unconscious strategies are expected to coexist in humans. return

REFERENCES

Barkow, J. H., Burley, N. (1980). Human fertility, evolutionary biology, and the demographic transition. Ethol. Sociobiol. 1, 163-180.

Bayliss-Smith, T. (1974). Constraints on population growth: the case of the Polynesian outlier atolls in the pre-contact period. Hum. Ecol. 2, 259-295.

Birdsell, J. B. (1953). Some environmental and cultural factors influencing the structuring of Australian Aboriginal populations. Am. Nat. 87, 171-207.

Birdsell, J. B. (1975). A preliminary report on new research on man-land relations in Aboriginal Australia. In (A. C. Swedlund, Ed.) Population Studies in Archaeology and Biological Anthropology: A Symposium. Am. Antiq. 40: pt. 2 memoir 30. pp. 34-37.

Blurton Jones, N., Sibly, R. M. (1978). Testing adaptiveness of culturally determined behaviour: Do Bushmen women maximize their reproductive success by spacing births widely and foraging seldom ? In (V. Reynolds and N. Blurton Jones, Eds.), Human Behaviour and Adaptation. Symposium No. 18 of the Society for the Study of Human Biology. London: Taylor and Francis, pp. 135-157.

Broom, L., Siegel, B. J., Vogt, E. Z., Watson, J. B. (1967). Acculturation: an exploratory formulation. In (P. Bohannon and F. Plog, Eds.), Beyond the Frontier. New York: Natural History Press, pp. 255-286.

Cant, J. G. H. (1980). What limits primates ? Primates 21, 538-544.

Cohen, M. N. (1977). The Food Crisis in Prehistory. New Haven: Yale University Press.

Dolhinow, P., McKenna, J. J., vonder Haar Laws, J. (1979). Rank and reproduction among female langur monkeys: Aging and improvement (They're not just getting older, they're getting better). Aggressive Behavior 5, 19-30.

Draper, P. (1976). Social and economic constraints on child life among the !Kung. In (R. B. Lee and I. DeVore, Eds.) Kalahari Hunter-gatherers. Cambridge: Harvard University Press, pp. 199-217.

Durham, W. H. (1976). The adaptive significance of cultural behavior. Hum. Ecol. 4, 89-201.

Gaulin, S. J. C., Konner, M. (1977). On the natural diet of primates, including humans. In (R. J. Wurtman and J. J. Wurtman, Eds.), Nutrition and the Brain, Vol. 1. New York: Raven Press, pp. 1-86.

Hallowell, A. I. (1949). The size of Algonkian hunting territories: a function of ecological adjustment. Am. Anthropol. 51, 35-45.

Hamilton, W. D. (1964). The genetical evolution of social behaviour I, II. J. theor. Biol. 7, 1-52.

Hardesty, D. L. (1977). Ecological Anthropology. New York: Wiley.

Hartung, J. (1976). On natural selection and the inheritance of wealth. Current Anthropology 17, 607-622.

Hayden, B. (1972). Population control among hunter/gatherers. World Arch. 4, 205-221.

Hayden, B. (1975). The carrying capacity dilemma: an alternative approach. In (A. C. Swedlund, Ed.) Population Studies in Archaeology and Biological Anthropology: A Symposium. Am. Antiq. 40: pt. 2 memoir 30. pp. 11-21.

Howell, N. (1979). Demography of the Dobe !Kung. New York: Academic Press.

Just, P. (1980). Time and leisure in the elaboration of culture. J. Anthropol. Res. 36: 105-115.

Lee, R. B. (1968). What hunters do for a living, or how to make out on scarce resources. In (R. B. Lee and I. DeVore, Eds.) Man the Hunter. Chicago: Aldine, pp. 30-48.

Lee, R. B. (1980). Lactation, ovulation, infanticide, and women's work: a study of hunter-gatherer population regulation. In (M. N. Cohen, R. S. Malpass and H. G. Klein, Eds.) Biosocial Mechanisms of Population Regulation. New Haven: Yale University Press, pp. 321-348.

Radcliffe-Brown, A. R. (1948). The Andaman Islanders. Glencoe: The Free Press.

Ricklefs, R. E. (1973). Ecology. Portland: Chiron Press.

Ripley, S. (1980). Infanticide in langurs and man: adaptive advantage or social pathology ? In (M. N. Cohen, R. S. Malpass and H. G. Klein, Eds.) Biosocial Mechanisms of Population Regulation. New Haven: Yale University Press, pp. 349-390.

Riss, D., Goodall, J. (1977). The recent rise to the alpha-rank in a population of free-living chimpanzees. Folia Primatol. 27, 134-151.

Schoener, T. W. (1971). Theory of feeding strategies. Ann. Rev. Ecol. Syst. 2, 369-404.

Slobodkin, L. B., Rapoport, A. (1974). An optimal strategy of evolution. Q. Rev. Biol. 49, 181-200.

Smith, E. A. (1979). Human adaptation and energetic efficiency. Hum. Ecol. 7, 53-74.

Southwood, T. R. E. (1977). Habitat, the templet for ecological strategies ? J. Anim. Ecol. 46, 337-365.

Stearns, S. C. (1976). Life-history tactics: a review of the ideas. Q. Rev. Biol. 51, 3-47.

Trivers, R. L. (1972). Parental investment and sexual selection. In (B. G. Campbell, Ed.) Sexual Selection and the Descent of Man 1871-1971. Chicago: Aldine, pp. 136-179.

Vayda, A. P., McCay, B. J. (1975). New directions in ecology and ecological anthropology. Ann. Rev. Anthropol. 4, 293-306.

Werner, O., Flowers, N. M., Ritter, M. L., Gross, D. R. (1979). Subsistence productivity and hunting effort in native South America. Hum. Ecol. 7, 303-315.

Wiens, J. A. (1977). On competition and variable environments. Am. Scientist 65, 590-597.

Wilmsen, E. N. (1979). Diet and fertility among Kalahari Bushmen. Working Papers No. 14 of the African Studies Center, Boston University. pp. 1-23.

Wilson, D. J. (1981). Of maize and men: a critique of the maritime hypothesis of state origins on the coast of Peru. Am. Anthropol. 83, 93-120.

Winterhalder, B. (1980). Environmental analysis in human evolution and adaptation research. Hum. Ecol. 8, 135-170.

A) Amplitude -- Some resource failures ('crunches') are worse than others, and if severe ones are common then minor ones may not even be perceived ('REAL'). For graphical simplicity I will consider only those which have an effect on the population, ignoring differences in amplitude among them ('IDEALIZED'). B) Period -- Crunches may occur in regular cycles (e.g., annually), irregular cycles (e.g., El Nino, mean interval 13 years, range 6-34 years (Wilson 1981)), or unpredictably ('REAL'). Again for simplicity, I will consider only moderately regular cycles ('IDEALIZED'; see text). C) L -- The duration of the mean interval between crunches that determine K. Beyond some upper limit (Lmax) each crunch is 'perceived' as unique. Crunches at intervals shorter than Lmin are 'perceived' as a single continuous event; intermediate intervals are the subject of this discussion.

Back to text

Lmin, the end of obligate offspring dependancy and/or the onset of offspring's ability to invest in kin; Lmax, which will vary according to the nature of selection (see text). The shape of the line between Lmin and Lmax is unknown and is expected to vary with phylogenetic and ecological variables. If Lmax/Lminis small, line 3 is most probable; if Lmax/Lmin is very large, line 1 is more likely to be appropriate. For most species, Lmin and Lmax are loosely correlated but this is not necessarily the case. The dotted line represents the importance of relatively density-independent/random morbidity and mortality. For humans, Lmin ~ 5 years and Lmax ~ 50 years (based on Howell 1979); for langurs (Presbytis entellus), Lmin ~ 18 months and Lmax ~ 20 years (based on Dolhinow et al. 1979). Note that for langurs parental investment is probably minimal by the time of offspring's reproduction, and a type (1) curve is expected (L ~ Lmin).

Back to text