Zoologiska Institutionen, Stockholms Universitet, S 106 91 Stockholm, Sweden
When an animal encounters a novel stimulus, be it in the wild or in the laboratory, we usually think that its initial behaviour in the new situation is determined by previous experiences with similar stimuli (either the animal's own experiences or those of its species, stored in its genes). This area of research has been referred to as `stimulus control' in comparative psychology, and `stimulus selection' in ethology. Both disciplines have produced similar results, although a comparison can be difficult because of differences in methods, terminology and scope [Hinde 1970,Baerends & Drent 1982]. Traditionally, ethologists have claimed that innate and learned behaviour are governed by different mechanisms, whereas psychologists ignored innate components of behaviour. Today, there seems to be little justification for any of these views. In fact, explanations in both fields share many common points, notably the assumption that responding is determined by similarity among stimuli. This applies, for instance, to psychological theories of stimulus generalisation and ethological theories of stimulus summation [Spence 1937,Hull 1943,Baerends & Krujit 1973,Shepard 1987].
The aim of our work is to contribute to a general theory of stimulus control that can bring together a number of different phenomena, and also allow a comparison between data from the field and the laboratory. The focus of this work is on the generalisation of stimulus-response associations to novel stimuli, and we will regard individual learning and evolutionary processes as two different ways of acquiring such associations. We describe a model able to predict responding and degree of generalisation given that certain associations have been established. An important advantage is that it provides an intuitive understanding of what to expect when stimulus-control is important, in contrast with e.g. artificial neural network models. In developing the model two steps are crucial. The first is to choose a space in which experiences and stimuli can be properly described. The second step is to specify how similarity among stimuli in this space determines responding. Most comparisons will be done with data from comparative psychology, the reason being that the animals' experiences are better known in such studies. We will, however, frequently point out similarities with ethological data.
How should we represent stimuli? A frequent method is to split them in a number of components that are somehow `self-evident' features of stimulation, for example lines, shapes or colours, in the case of visual stimuli. This is done in a number of theories, e.g. stimulus sampling theory [Atkinson & Estes 1963] and feature theory (for example in [Rescorla 1976] ). An even simpler representation is to just note the presence or absence of components such as a light or a tone. How to identify the features of stimulation themselves is however a rarely addressed question. One approach, adopted mainly in human psychology, is to locate stimuli in a psychological space [Shepard 1987,Shanks 1995]. This procedure, in short, amounts to presenting subjects with a number of stimuli and measuring how often they make mistakes in telling the different stimuli apart. The stimuli are then positioned in an abstract space via a statistical analysis so that their distances reflect the similarity judgments made by the subjects. The coordinates in this space can be frequently interpreted, a posteriori, as corresponding to meaningful physical characteristics of the considered stimuli (e.g. brightness and saturation for a colour classification in [Nosofsky 1987] ). This approach is useful to determine the relations among stimuli as they are perceived by the subjects, but it is clear that in this way the space is built according to the observed behaviour. Our concern here, instead, is to have a space which allows us to predict behaviour as a function of stimulation.
The approach we follow is to start from how stimuli appear at the receptor level. External stimuli affect the sense organs by activating receptor cells. Stimuli that differ only for the value of one physical parameter are said to lie on a `stimulus dimension', for instance wavelength or intensity of light. If stimulation changes along such a dimension the activation of sense organs changes in a charactersitc way. It is useful to distinguish between two basic types of dimensions. One example of the first type is light wavelength: photoreceptors have maximum sensitivity to one wavelength, and react progressively less when stimulation departs from this value. The second type is intensity dimensions, where there is no peak in sensitivity: a more intense stimulus always yields a stronger activation. We will see that this distinction has important consequences for stimulus control.
For simplicity, we consider a model perceptual organ made of N cells, that react to stimulation by emitting an output signal, taken to be a number between zero and one. A stimulus s is then represented as the collection of activities si , i = 1,¼,N , produced in each of the receptor cells. We call the receptor space, R , the space spanned by all possible patterns of activation.
A theory of stimulus control aims to express the rate of responding to novel stimuli in terms of their relations to those stimuli that have been experienced in the past, given that we know how the experienced stimuli are reacted to. Thus, once stimuli have been represented in some space, we need a means to express the `relatedness' of different stimuli. In the framework of a `feature' decomposition of stimuli, as recalled in the preceding section, it is customary to measure the similarity of two stimuli according to the number of equal features they share. In the case of psychological spaces, the assumption that the perceived similarity between two stimuli is a function of their distance in the space is crucial for the very construction of the psychological space itself.
In the receptor space R it is possible to consider many different ways to relate stimuli one to the other. It proves useful to use the following definition for the `relatedness' of any two stimuli, say a and b , that we note a·b :
| (1) |
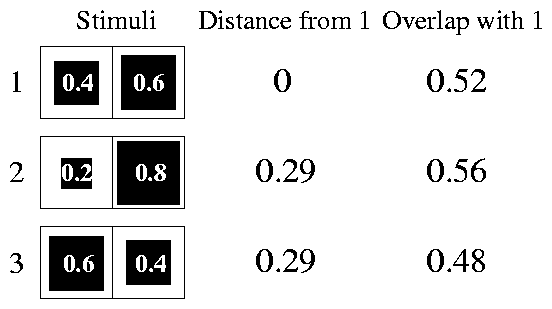
Note that the overlap 1 is not a measure of similarity in the mathematical sense, since there is the possibility that, e.g., a·b > a·a , so that a overlaps with b more than with itself. By contrast, the similarity of an object to itself has to be greater than the similarity of the same object to all the others that can be considered. This property can be equivalently expressed in terms of distances: the stimulus that is closest to a is always a itself.

For example, it can happen that a·b > a·a if b , in addition to producing a similar activation pattern, also activates some cells to a greater extent than a . We illustrate this point in 1, that represents three very simple stimuli and the overlaps and Euclidean distances of each of them with the first one. The stimuli are imagined to act on a sense organ with only two receptors. We see that, although stimuli two and three have the same distance from one, they have different overlaps with it, and that stimulus two has a bigger overlap with one than one itself. This latter property reminds us of the peak-shift phenomenon, observed under certain conditions when an animal, reinforced for responding to a stimulus S+ , is found to respond with maximum strength to a stimulus that is different from S+ (we use uppercase letters to refer to real stimuli, and lowercase ones for stimuli in the space R ). This point will be more deeply analysed below.
What is the advantage of using overlaps instead of distances? The main problem of distances is that they do not take correctly into account the intensity of stimulation. Since similarity can always be expressed in terms of distances, this inability has serious consequences for all theories that base responding on similarity. Consider for example a positive stimulus S+ . The fact that no stimulus can be more similar to S+ than S+ itself means that response should decline if we change S+ in any ways (in the absence of other relevant experience). But we know from experiments that changes that yield more intense stimuli will also produce a stronger response (see the following for references and comments). This holds for any space that we choose to represent stimuli in, be it a psychological space, a feature space or the receptor space R we use here. We can interpret overlaps as combining information about distances and intensities. Given two stimuli a and b , the following relation connects their overlap a·b with intensities and Euclidean distance d(a,b) :
| (2) |
Suppose that an animal has experience with two stimuli, S+ and S- . As the notation suggests, we can imagine that S+ is a positive stimulus, i.e. associated with a reward, while S- is a negative or neutral stimulus, so that the animal responds more to S+ than to S- . In the framework of stimulus control, we want to express the rate of responding to other stimuli in terms of their relations to S+ and S- . We have of course to suppose that no strong pre-existing bias is affecting responding, coming from previous experiences or species characteristics. To keep things simple we suppose as well that, in the model, responding can be considered a continuous variable of stimulation, so that r(s) is the strength of the response to stimulus s . If s+ and s- model S+ and S- , then r(s+) > r(s-) . For example, we can consider r(s) to vary between 0 and 1, and interpret it as probability of response to s . A comparison with reality can then be made in terms of number of responses or response frequencies. 0000
Note that we do not consider how a stimulus-response association has been acquired. What we want to predict, instead, is generalisation given that certain stimulus-response relationships have been established. Throughout this paper, s+ means a stimulus which yields a high response, while a low response is assumed for stimuli noted as s- . This is not to dismiss learning or evolution as unimportant, but rather to explore those characteristics of stimulus control that are independent from the details of the acquisition process (see the Discussion).
If the definition 1 is meaningful, we can expect that responding to a stimulus s is determined as some function of the overlaps of s with s+ and s- . Without considering any specific model of learning and memory, it is difficult to say anything about such a function, apart that when s is very close to s+ or s- the conditioned response should be reproduced. A working hypothesis can be stated as follows:
if s·s+ > s·s- , that is if s overlaps more with s+ than with s- , then the response r(s) should be closer to the one associated with s+ , and vice versa if s·s+ < s·s- .
For brevity, the above assumption will be referred to as the overlap principle. It is exactly the translation in the present context of the statement that similarities to the conditioned stimuli should determine responding. The only difference is that 1 is assumed as a means to relate stimuli to each other.
In the present case, having assumed r(s+) > r(s-) , we can consider the difference
| (3) |
Note that d(s) provides us with a ranking of the different stimuli, and not with absolute response rates: it enables us to predict that, in a given situation, bigger values of d(s) correspond to higher response rates. So, 0000d(s) is not the same as the strength of the response r(s) , but there is a definite relation between the two: if d(a) > d(b) , then r(a) > r(b) , for any two stimuli a 0000 and b . Already the knowledge of the rank of stimuli provides us with all information about the position of a peak, the shape of a gradient and its symmetry or asymmetry.
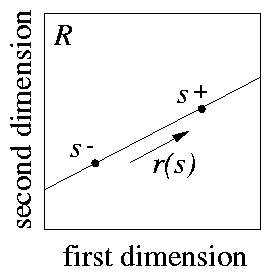
We are assuming that only two stimuli, s+ and s- , have been associated with a response. These two stimuli determine a dimension: the line that joins them (see 2). We will refer to a generalisation test along this dimension as a `line test'. It is important to remember that this line is meant to be in the receptor space R ; we will discuss later on how to relate it to physical stimulation. To derive predictions about this test, we have to calculate d(s) along the line. This can be done by introducing a coordinate x so that to each value of x corresponds one stimulus s(x) on the line. The mathematical representation of s(x) is very simple: the activation of each unit si(x) is given in terms of the activations of the corresponding units s+i and si- by:
| (4) |
Using 4 we can write d(s) , from its definition 3, as follows:
| (5) |
Although the line test may look abstract, there is one case in which a familiar generalisation test corresponds directly to it, namely the case of intensity generalisation. This can be seen with the help of 3, representing the effect of two stimuli on a sense organ with 10 receptors.

The four central units, that differ between s+ and s- , model what is controlled by the experimenter, e.g. a light or sound whose intensity can be varied. The lateral units represent contextual stimuli, that is aspects of the experimental environment that are never varied during the experiment. Moving along the line that joins these two stimuli, following equation 4, amounts to simultaneously change the intensity of the central units. For example, values of x greater than one will produce more activity than s+ , resulting in a more intense stimulus. Experimental results from intensity generalisation tests (see 4b) conform indeed to the above predictions: they increase monotonically moving from the negative to the positive stimulus and show positive as well as negative shifts [Razran 1949,Thomas & Setzer 1972,Huff et al.Huff, Sherman & Cohn 1975,Zielinski & Jakubowska 1977]. Some non-monotonicity is sometimes found, but we must keep in mind that we are considering the idealised case in which only s+ and s- contribute to responding. In reality many experiences, both learned and inherited, influence the animals.
Intensity generalisation has also been studied in ethology, with similar results. One example is the preference of gulls (Larus argentatus) towards brighter egg dummies, reported in [Baerends & Drent 1982]. In choice tests between two dummies placed on the nest rim, the lighter of two shades of gray was consistently preferred. The only exception to this pattern regarded the white dummy, that was not reliably preferred to darker shades. The study from [Tinbergen 1942] also reveals a monotonic gradient. Male grayling butterflies (Eumenis semele) were shown female dummies of different shades of gray, and the darker the dummy, the more pursue flights it elicited (reversed intensity generalisation, see below).
In the model as in experiments [Huff et al.Huff, Sherman & Cohn 1975,Zielinski & Jakubowska 1977], it does not matter which one of s+ and s- is the most intense: the gradient appears reversed if stimuli are aligned according to intensity (4, descending lines), but does not change in the geometrical representation, always growing from s- to s+ (the direction of increasing x ). Note that the prediction of monotonic gradients depends only on the fact that receptor activation increases with physical intensity, not on the precise nature of the increment. We have assumed above that such increase is linear, while it is usually logarithmic citep{cor89,bru96}. However, intensities are usually measured on logarithmic scales (as in 4 for noise intensity, measured in dB), so that receptor activation increases linearly along the scale.
Intensity generalisation is only a particular case of `line test', and one can use other stimuli as s+ and s- that do not have a well-defined intensity relationship. For example, s+ can be more intense than s- on some receptor cells but less so on other ones (see 5). According to the overlap principle, we get the same predictions as before under these more general conditions: a monotonic gradient increasing from s- to s+ with both positive and negative shifts in responding. This is a novel prediction, and it can be tested experimentally. To design such an experiment we need to build a set of real stimuli that can be considered to lie on a single line in the receptor space associated with a sensory organ. A simple possibility is to have two white lights to generate the stimuli. Let us indicate their intensities with two numbers, so that S = [l,L] means that the stimulus S is produced by activating the first light to an intensity of l (measured in some appropriate scale), and the second light to an intensity of L . Let us have S+ = [l,L] and S- = [L,l] as training stimuli. We can then generate a set of test stimuli by choosing the intensities of the two lights in agreement with 4:
| (6) |
The experiment reported by [Koehler & Zagarus 1937] can be considered of this kind, although it does not provide conclusive evidence. They presented ringed plovers (Charadrius hiaticula) with normal eggs (dark brown speckles on a light brown background) and artificial dummies. The dummies had black speckles on a white background, and were preferred over the normal ones. This preference agrees with our analysis if we consider the natural egg as a positive stimulus, and the background of the nest (which is brown-gray sand or gravel) as the negative one. This natural situation can be modelled with a uniform s- (all units with the same intermediate activation) and an s+ which is a mixture of highly and low activated units. Then the `preferred' region of the line, where x > 1 , corresponds to stimuli in which the contrast with the s- is enhanced: where s+ is lighter (darker) than s- , a supernormal stimulus should be even lighter (darker). Since tekoe37 did not test other dummies, however, our conclusion must be considered provisional. It can be thoroughly tested by investigating the ringed plover's preferences over a wider range of speckling-background contrast. For example, our model predicts that a normal egg should be preferred over one of uniform colouration close to the nest background. This latter colouration, in turn, should be chosen more often when confronted with an egg with a dark background and light speckles (the converse of the supernormal appearance, corresponding to x < 0 in the model).
Most generalisation gradients look different from those obtained in intensity generalisation tests in that they are not monotonic, often presenting a peak at or near the positive stimulus [Guttman & Kalish 1956,Kalish & Guttman 1957,Hanson 1959,Kalish & Guttman 1959,Jenkins & Harrison 1960,Jenkins & Harrison 1962,Marsh 1972]. This can be understood by realising that, although the experimental stimuli can be lined up on a single dimension (for example, sound frequency or light wavelength), this dimension is not a straight line in the receptor space.
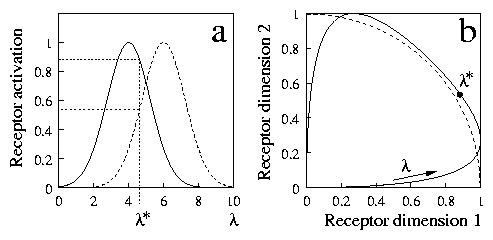
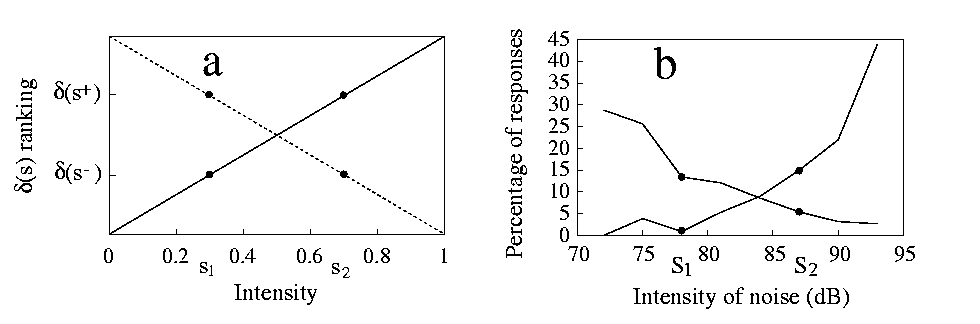
We illustrate this fact in the idealised case of a receptor organ with two cells. Imagine for example that these are two photoreceptors, that respond maximally to two different wavelengths, but also to other ones, as depicted in 6a for a dimension named l. The first receptor responds better to lower values of l, while the second one is more active at higher values. We can probe this receptor organ with stimuli of different `wavelengths', and the resulting stimulation can be represented in a two-dimensional graph, as we show in 6b. Each point in the graph represents a pair of activations of the two receptors. When l steadily increases, the representative point moves in the receptor space, describing the solid curve in 6b. This curve is the representation of the l dimension in terms of receptor activations. The figure also shows (dashed line) a curve of constant intensity (these curves are arcs of a circle, in the model). We see that part of the l dimension is close to this curve, so that the intensity of stimulation is approximately constant for many values of l.
All the results we describe in the following are largely independent of the exact form of the receptor response functions, and of the number of cells one considers. What is important is that the receptor activations are peaked at some value along the considered dimension, and react progressively less when departing from it. This is true of many receptors when stimulation varies along common stimulus dimensions. A further example, in addition to photoreceptors, are ganglion cells in the ear, whose response curves are similar to those in 6a, often reacting to a range of sound frequencies of several hundreds Hz (see [Coren & Ward 1989] ). In this way, even a tone consisting of a single frequency elicits responding by many ganglion cells. Two tones of not too different frequencies generate overlapping activation patterns. With this model of perception, and the overlap principle, we can predict the shape of generalisation gradients along these dimensions.
We expect a peak in the gradient when d(s) first increases and then decreases along the test dimension, with the peak located where d(s) is at a maximum (this point will be examined in detail when addressing the phenomenon of peak-shift below). This is indeed what happens if the action of physical stimuli on the sense organ is modelled as described above. In 7a we show the model results for a receptor organ made of 50 cells with response functions as those in 6a, evenly spaced along a dimension. While s+ is a stimulus along this dimension, we have assumed s- to elicit a very small activation in each cell, so that it can be interpreted as absence of stimulation in the considered sense organ (e.g. silence in the case of sound). In this way we have a situation like, for example, that investigated by [Jenkins & Harrison 1960], that trained pigeons to respond to a 1000-Hz tone but not to silence.
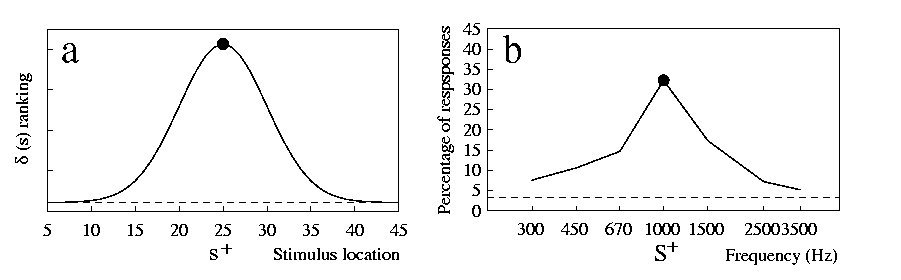
The data reported in 7b, from [Jenkins & Harrison 1960], show the good agreement of the results from this study and the model. Similar findings with other dimensions and species are reported, for example, by [Hanson 1959] pigeons, light wavelength, [Brennan & Riccio 1973] rats, sound frequency, [Galizio & Baron 1976] humans, sound frequency. The precise shape of a gradient is determined by the characteristics of the stimuli employed, as well as by the response properties of the receptor cells. For example, the width of the peak (i.e. the amount of generalisation) depends on what stimulus range the receptor cells react to (that is the width of the curves in 6a in the model). A more accurate model than the one presented here may be able to account for asymmetries, steepness or other characteristics of gradients.
In this section we consider the conditions under which peak-shift or supernormal stimuli are expected. We already saw one case in which the maximum responding was not elicited by the training stimulus or the natural stimulus (4.1). In general, we expect a stimulus s to be supernormal if it yields a bigger d value than s+ , that is d(s) > d(s+) . Here we examine two typical cases where, in contrast to 4.1, the intensity of all test stimuli is approximately the same in the range of stimulation employed (see 6b). These are non-differential training and discrimination training along dimensions such as light wavelength or sound frequency. We show that the model predicts correctly the finding that only discrimination training produces peak-shift.
Consider first non-differential training. In the previous section we examined a case where responses to a tone were rewarded but responses to silence were not [Jenkins & Harrison 1960]. Since silence had the same overlap with all test frequencies, the contribution of s- to d(s) can be discarded. For s to be a supernormal stimulus we need then s+·s > s+·s+ , but this is not possible if s has the same intensity as s+ . This agrees with the empirical data on non-differential training [Hanson 1959,Marsh 1972,Galizio 1980]. The same conclusion is true when s- produces a strong but uniform activation throughout the considered array of cells, for example in the case of white noise as opposed to tones of different frequencies [Baron 1973].
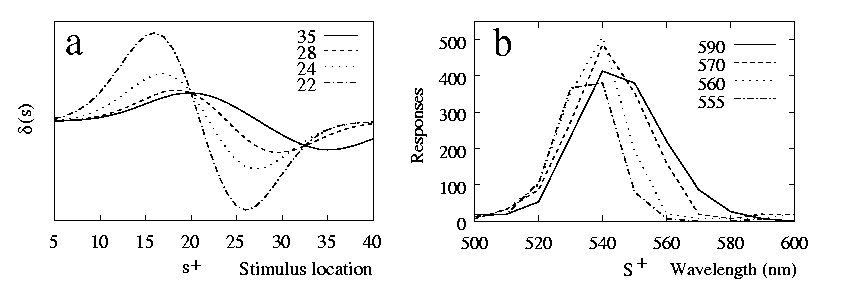
By contrast, after discrimination training peak-shifts are usually found [Marsh 1972,Purtle 1973,Rilling 1977,Ohinata 1978]. A classical example is the study by [Hanson 1959] along the dimension of light wavelength, whose data are reproduced in 8b. A change in wavelength causes a change in the relative activations of photoreceptors in the eye, while the total intensity is roughly unchanged. This is also what happens in the model of perception in 6 as stimulation varies along the model dimension l. To model discrimination we choose an s+ and an s- which lie along this dimension. The results are shown in 8a, where d(s) is plotted for four cases in which s+ is fixed, while s- has different locations along the model dimension. When the negative stimulus is far away from (i.e. overlaps little with) s+ , no peak-shift is found. When s- is close enough, d(s) is not maximised at s+ and a peak-shift is observed. The closer the training stimuli, the further away from s+ the peak is pushed. The qualitative agreement with Hanson's (1959) experiment is clear.
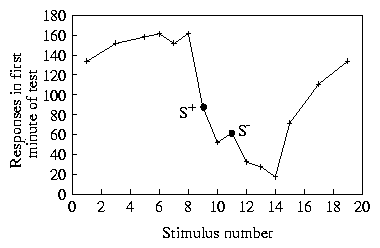
A seeming disagreement between the d gradients and the experimental ones is that from the d gradients one expects as much negative as positive peak-shift (8a). A negative peak-shift is present as well in Hanson's (1959) data, but it is strongly masked by the floor effect resulting from very low responding to S- . One possible means of showing that the negative stimulus is preferred to other stimuli, that are further away from S+ , would be to present the animals with a choice between S- and the candidate stimulus. Another way, as done in [Guttman 1965], again in the case of wavelength, is to raise the baseline of responding along the whole dimension, by reinforcing responses to keys of many colours. Guttman then introduced a discrimination training reinforcing one colour but not a second one. Not even these results are entirely free of floor effects, but a clear negative peak-shift can be appreciated (9). Similar results were also obtained via a slightly different procedure by [Stevenson 1966].
Peak-shift phenomena along non-intensity dimensions have been found in the wild as well. For example, many studies have studied the influence of the egg colouration on the egg-retrieval behaviour of birds, e.g gull species (L. ridibundus in tebae75 1975; L. argentatus in 1982). In these studies at least one colour was found to be more effective than the natural egg colour. These preferences can be intepreted as peak-shifts arising from a discrimination between the egg and the nest background (see also 4.1.2). Another example comes from zebra finches (Taeniopygia guttata), a species in which sex recognition is acquired early in life based on the appearance of the parents. However, tevos95 has showed that the beak colour preferred by males is not that of the mother, but it is shifted away to depart from the father's beak colouration.
We examine two possible extensions of our model. First of all, a viable model should ultimately be able to take into account experiences with many stimuli. When more than two stimuli control responding, it is not enough to use the d function in equation 3 to infer generalisation gradients. The overlap principle is nevertheless easy to generalise to an arbitrary number s of stimuli. Suppose that a response ra has been established to stimulus sa , that is ra = r(sa) , for a number of stimuli a = 1,¼,s. We can then say that, given a stimulus s , the response r(s) will be `closer' to that response for which the corresponding overlap s·sa is greatest. The precise meaning of `closer' cannot be defined without reference to a model of acquisition and memory, but generalisations of 3 can be formulated on the basis of heuristic principles (see below for a simple example).
A second important step yet to be made is to go from a qualitative model to a quantitative one. In introducing the d function, we have said that it provides us with the ranking of stimuli. It would be a significant improvement to be able to predict responding quantitatively. Although we have only considered the ranking properties of d so far, it is also apparent that the d curves are very similar to the corresponding generalisation gradients. This suggests that d may provide something more than rankings. A simple but valuable step in this direction can be to focus on relative response strengths. That is, we can assume that if d(s) is two times as big as d(s+) , the response to s will also be roughly two times the response to s+ .
We illustrate these two lines of development in a simple case, that of two positive stimuli and a negative one. [Kalish & Guttman 1957] have studied this situation in the pigeon, using light wavelength as a dimension. They found that the gradient changes shape when the distance between the positive stimuli is varied. When the stimuli are far apart, two distinct peaks are observed, but when their distance is reduced the gradient peaks at an intermediate point (10b).
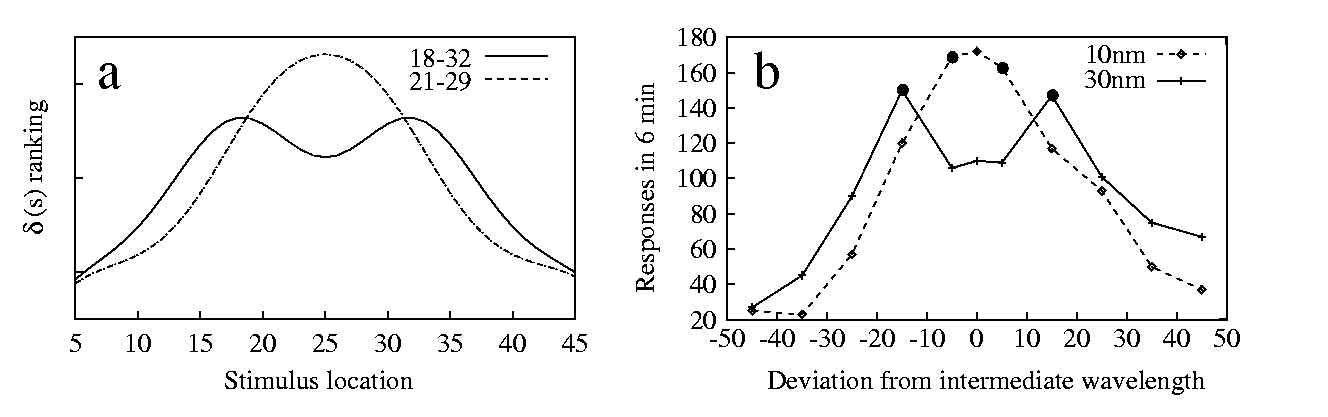
If we suppose, for simplicity, that the training procedure and responding are the same for the two positive stimuli, a straightforward generalisation of 3 is:
| (7) |
There are still some difficulties with these extensions of our model. For example, it is not yet clear how to define an appopriate d function when an arbitrary number of stimuli has been experienced, each yelding possibly a different response. Also, the relative d values can be bigger than 1 or smaller than 0, so that in these cases they cannot be directly interpreted as response strengths. We have, however, seen that d can indeed reveal some `hidden structure' of gradients that is not apparent due to floor or ceiling effects (see 8 and 9). In conclusion, there is still a lot to do. We hope to have shown that there are concrete possibilities of development.
In this paper we have introduced a general model of stimulus control able to account for various findings regarding generalisation, including the phenomena of supernormality and peak-shift. The main results that we have obtained are the following: (a) the amount of generalisation and the shape of gradients are not assumed but emerge from the model; (b) gradient shapes and the occurrence of supernormality and peak-shift can be investigated along any dimension, because one can always compute the overlap between any two stimuli given knowledge of receptor response properties; (c) the model can account for all known kinds of peak-shift, including the open-ended shift found in intensity generalisation.
The best known model of stimulus control is the Spence-Hull theory of gradient interaction based on [Spence 1937,Hull 1943] . This theory postulates that responding can be predicted by combining individual `excitatory' and `inhibitory' response gradients. Each individual gradient is the consequence of experiences with a particular stimulus (positive or negative), and is assumed to be bell-shaped and to peak on the experienced stimulus.
The greatest merit of Spence and Hull's theory is that different experiences interact to control responding. This interaction can have important consequences, such as peak-shift. The theory has however shortcomings. Its two basic ingredients are the shape of the elementary response gradients and the rules of their interaction. Both things have to be assumed. In early works, gradients were assumed to be bell-shaped, and to interact simply via algebraic summation. It is now clear that both assumption must be modified in many cases. For example, it is not possible to obtain the monotonic response gradients characteristic of intensity dimensions by combining bell-shaped ones. Likewise, [Kalish & Guttman 1957,Kalish & Guttman 1959] have shown that algebraic gradient summation does not predict correctly responding after training with two or three positive stimuli.
The approach presented here overcomes these difficulties. The shape of gradients emerges from the model, and can be understood as stemming from overlaps of activation patterns in the sense organs. We have also seen that generalisation after training with two positive stimuli is well predicted by the model (5), although more work is necessary to take into account more complex experiences.
A few other models base their predictions on the analysis of overlapping sets of features among stimuli [Atkinson & Estes 1963,Rescorla 1976,Pearce 1994]. The most interesting is the learning model by [Blough 1975]. In this model each physical stimulus activates a number of abstract elements in the animal. The response is determined by these activations and by generalisation factors. Generalisation occurs because similar stimuli produce similar activation patterns. This model can generate realistic generalisation gradients, including peak-shift. A problem with Blough's model is the elements: it is not clear what they correspond to in reality. Blough himself noted that this is `unfortunate' since `the stimulus elements become hypothetical'. This means that it is not easy to incorporate knowledge about perception in the model. Furthermore, the generalisation factors assumed by Blough cannot account for intensity generalisation.
Our approach does not have these problems, since we take the interaction between stimuli and sense organs as the starting point. The representation of stimuli as activating many receptors is not arbitrary, and we can determine the activation pattern produced by any physical stimulus by studying how the physiology of sense organs. For example, we have seen that there is a clear difference between increasing the intensity of a monochromatic light or its wavelenght. This difference cannot be discovered a priori, but needs knowledge of perceptual processes. Given this knowledge it should be possible to extend Blough's model so that it also deals with intensity effects, although this was not noticed by Blough (Ghirlanda & Enquist, unpublished data).
The model presented here has a few points in common with some artificial neural netwok models. The question of what space to consider to represent stimuli is crucial when building such models, too. It is natural to identify the receptor space R with the input layer of the network, rather than providing the network with `features' or other abstract inputs. Following this approach, and with the same modelling of perception used here, we have obtained detailed accounts of generalisation phenomena in the case of simple network models, in full agreement with the overlap principle [Ghirlanda & Enquist 1999]. There is an important difference in approach between neural network models and a model like the one presented here. The overlap principle is an explicit statement about how experiences interact to control behaviour (via overlaps). A neural network model is built more or less in the opposite way. It is a low-level model of the nervous system, and its stimulus-control properties emerge from its computational principles, but are not apparent from the outset. We can say that the overlap principle tells us what is computed, but not how; conversely, a network model is an explicit model of how stimuli are processed, but we are not sure from this alone what will be computed. While neural network modelling has the possibility to resemble closely real nervous systems, abstract models (such as the overlap principle) can provide us with understanding of what the system is actually doing. For these reasons, we reagard these two approaches as complementary, rather than antagonistic: knowing what information an animal takes into account in directing its behaviour can be of valuable help in designing and testing new neural network models. Moreover, it is difficult to acquire an intuitive understanding of neural networks model, due to their complexity. It is therefore convenient to have simpler models that are easy to get intuition for. For example, in designing an experiment where generalisation is expected to play a role, it is easier to think about how much stimuli overlap with each other on the animal's sense organs, rather than running neural network simulations with several different stimulus configurations.
It is clear that our model cannot explain all findings, in its present form. For instance, the case of line-tilt generalisation experiments [Hearst 1968] is problematic. The gradients obtained are entirely similar to those coming from, e.g., wavelength or tone-frequency generalisation, but all positions of the tilted lines overlap in the same little region near their centre. One way of developing the model could be to allow for more refined preprocessing of stimulation. This preprocessing would provide us with a transformed space where the overlap principle can be applied. This space would contain representations of the input stimuli that reveal more readily information about, for instance, angles or shapes. This can be done by combining stimulation from a number of receptor cells. In the case of line tilt, we can consider cells that combine the stimulation from a number of neighboring cells in the sense organ (receptive fields). Such an arrangement would be able to replicate data from line-tilt generalisation, since the more the line is tilted from the S+ position, the less receptive fields are in common with S+ .
Another problem that the model cannot presently account for is the famous XOR (exclusive or) problem (responding to A or B but not to AB or absence of stimulation). However, this is due to the simplicity of the d functions used in this paper, and it is not an intrinsic limitation of the overlap approach. For example, appropriate preprocessing can eliminate this shortcoming. It seems important here that the preprocessing we apply corresponds to reality. One reason why we have considered only sense organs is that we do not know with sufficient accuracy how neurons beyond the first few layers are activated by external stimuli (another reason was to investigate how much can be predicted by only considering properties of sense organs). The risk of too bold an attitude is to assume as outputs of an unknown preprocessing system precisely those `self-evident' features that we felt the need to abandon, e.g. building a model whose inputs are labelled `stimulus A', `stimulus B', `combination of A and B' and so on.
Our model is about retrieval from memory, but not about memory changes. This brings up an important issue: if responding to the experienced stimuli is the same after two different acquisition processes, will this also be true for responding to novel stimuli? In our model, generalisation does not depend on the details of the acquisition process, but only on the established responding to s+ and s- . The underlying assumption is that all acquisition processes, given that they establish the same stimulus-response associations, will result in similar changes of memory, leading to the same patterns of generalisation. Despite this simplification, our model can account for a number of stimulus-control phenomena. This strengthens the belief that experience is coded in similar ways irrespective of many factors, such as species, sensory modality, relative importance of learned and innate components of behaviour.
However, there is also a number of findings showing that the details of the acquisition process can be important. One such example is the phenomenon of blocking (see [Mackintosh 1974] [van Kampen & de Vos 1995] have shown the effect also in filial imprinting in junglefowl chicks). We can establish responding to a compound stimulus AB (for example, a light and a tone) in two different ways. One is simply to reward responses to AB , the other is to reward first responses to A alone, and then to the compound. If we present now B alone, we find that the former procedure results in stronger responding than the latter, even if responding to AB was the same. It is said that prior experience with A has `blocked' learning about B . Our model can account only partially for this finding. Blocking is predicted to some extent because in the case of A , AB training the animal has less experience with B (relative to the total experience), compared with AB -only training. But this effect would be the same after AB , A training, which is at odds with current theories of blocking. We do not know, however, of any studies of blocking using the control procedure AB , A .
In this paper we have presented a new way of analysing stimulus control. The approach seems to offer several advantages, and we can envision a number of ways in which the model can be used. First of all, the model is based on a simple principle that can be applied widely. Stimuli are represented in a way that requires no arbitrary constructions: this allows us to model each real situation and to explore generalisation along any dimension. Furthermore, we can explain and compare findings from both field and laboratory experiments, and apply the model to both innate and learned behaviour.
The model can also be used as a guide for what to expect when stimulation is important, for instance in studies of sexual selection or signal evolution. It can also be a starting point in proximate studies of behavioural mechanisms. For example, the model itself generates novel predictions that can be brought to empirical testing (see 4.1). In proximate studies it is important whether overlaps can explain responding or whether additional factors have to be taken into account. We saw above at least two cases in which the overlap principle was not sufficient (line-tilt generalisation and blocking). This calls for further development.
Especially in ethology, the interest for mechanistic studies of stimulus control has faded in recent years. It is time to take up these studies again.
We thank Björn Forkman, Gabriella Gamberale, Peter L. Hurd, John M. Pearce and five referees for useful criticism on earlier versions of the manuscript. Thanks also to Francesco Guerra for useful discussions and Wolfgang Engelmann for help with the bibliography.
1 Published in Animal Behaviour 58(4), 695-706. © 1999 The Association for the Study of Animal Behaviour. Permission to copy and redistribute in any media is granted to everyone provided no fees are requestred and no alteration is made. Please encourage and support the free distribution of scientific papers (see for instance http://rerumnatura.zool.su.se). Minor language differences may be found with respect to the published version.
NOTE: This file has been translated to HTML from the original in LaTeX format. This process is not perfect and some funny things may be around. We apologise with the reader. Printer-ready versions can be obtained from the authors' web page.
File translated from TEX by TTH, version 2.51.
On 11 Oct 1999, 14:09.