Block, Ned (1996) Anti-Reductionism Slaps Back. To appear in Philosophical
Perspectives.
Anti-Reductionism Slaps Back
For nearly thirty years, there has been a consensus (at least in English-speaking
countries) that reductionism is a mistake and that there are autonomous
special sciences. This consensus has been based on an argument from multiple
realizability. But Jaegwon Kim has argued persuasively that the multiple
realizability argument is flawed.1
I will sketch the recent history of the debate, arguing that much --but
not all--of the anti-reductionist consensus survives Kim's critique. This
paper was originally titled "Anti-Reductionism Strikes Back",
but in the course of writing the paper, I came to think that the concepts
used in the debate would not serve either position very well.
Multiple Realizability
Fodor and Putnam initiated the anti-reductionist consensus thirty years
ago by noting the analogy between computational states and mental states
(Fodor, 1965, 1974; Putnam, 1965, 1967). Any computational property can
be "realized" or "implemented" in a variety of ways
(electronic, mechanical, hydraulic), so it would be a mistake to identify
any computational property with, say, an electronic property, since the
same computational property can be implemented without the electronic
property, for example mechanically. If thought is computational or functional,
then for the same reason it would be a mistake to identify thought with
any neural state; for thought can be implemented non-neurally, e.g. electronically.
It would be wrong to identify thinking with a brain state if a device without
a brain could think.
I have put these points in terms of identity. Computing square roots
is not identical to any electronic property, pain is not a brain state,
etc. But reduction is not quite the same thing as identity. According to
a variant of a commonly accepted analysis (Nagel, 1961), a theory U (for
upper level) is reducible to a theory L (for lower level) if and only if
the terms of U are "definable" in terms of L, and the
laws of U are explainable (or approximations to them are explainable)
by the laws of L plus definitions. The "definitions" can be seen
as identities (temperature = mean molecular kinetic energy), but it is
usually supposed that they can also be seen as nomic equivalences (by nomic
necessity, the value of temperature is a known constant times the
value of mean molecular kinetic energy). These definitions are often called
bridge principles or bridge laws. The important point is that the multiple
realizability observation applies to reduction, on either way of construing
the definitions. If thinking is not even coextensive with any neurological
property, then the term 'thinking' is not definable neurologically and
so psychology is not reducible to neurophysiology. The difference between
seeing the definitions in terms of identity as opposed to nomic equivalence
will not loom large in this paper.
I keep speaking of realization. What is it? As Kim notes, we can think
of realization this way. Suppose we have a family of interconnected macro-properties
(e.g. mental properties or economic properties) of a given system (say
a person). Suppose that corresponding to each of these macro properties
there is a micro property in this system, and that the family of interconnected
micro properties provides a mechanism for explaining the connections among
members of the macro family. Then the micro properties realize the macro
properties. (Of course, this talk of macro and micro is relative; properties
that are micro relative to to one set of properties can be macro relative
to another.)
Fodor and Putnam were reacting against the Unity of Science movement,
a positivist ideology whose ultimate expression was Oppenheim and Putnam
(1958), "Unity of Science as a Working Hypothesis". Oppenheim
and Putnam divided all of science into levels, starting at the bottom with
elementary particles and building up to molecules, cells, individuals,
and societies. They argued that the science at each level was reducible
to the next lower level, and thus that the laws of micro-physics are the
basic laws of all sciences. By contrast, Putnam and Fodor advocated what
might be called the Many Levels doctrine, the view that nature has joints
at many different levels, so at each level there can be genuine sciences
with their own conceptual apparatus, laws and explanations. Fodor's (1974)
key article emphasizing the autonomy (which we can take to be just irreducibility)
of the special sciences was subtitled "The Disunity of Science as
a Working Hypothesis".
An illustration (see Block, 1995) of the Many Levels idea appeals to
explanations of how a computer works at different levels. Suppose that
a computer makes an error that is explainable in terms of a glitch in a
program. The explanation in terms of the glitch is more general than a
hardware account in that it holds of all computers that run this program
no matter what the hardware. However, the hardware level will itself be
more general in allowing explanations of computer errors due to vibration,
a factor that is invisible at the program level. And the hardware level
allows us to see similarities between different sorts of machines that
use the same hardware but are very different at the program level. For
example, a programmable computer may use much the same hardware as a dedicated
word processor. Another influential analogy was Putnam's (1975) explanation
of why a solid rigid round peg 1 inch in diameter won't fit through a square
hole in a solid rigid board with a 1 inch diagonal. We can contrast the
"upper level" explanation in terms of solidity, rigidity and
geometry with the "lower level" account in terms of the specific
elementary particle constitutions of a specific metal peg and wooden board.
The upper level account is more general in that it applies to any solid
rigid peg and board with that geometry, including materials that are composed
of glass (a supercooled liquid) instead of the lattice structure of metals
or the organic cell structure of wood. But the lower level account is more
powerful in that it explains the specific cases of solidity and rigidity
themselves. Further, it is more general because it explains details of
the interaction between the peg and the board, including cases where the
peg crumbles or the board breaks or tears.2
Multiple realizability often applies within and between individual people.
For example, the central nervous system is often supposed to be quite plastic
(though recent results appear to challenge this long-held view), especially
in the young. If the brain is injured, knocking out some capacities, the
capacities often reappear with different neural realizations. And there
are many states and capacities that are known to be implemented differently
in different people, e.g. the capacity to read. The multiple realizations
are often themselves multiply realized, a fact that I will sometimes ignore
in this paper for simplicity, talking as if each special science has only
one level of realization, the physico-chemical level.
Heterogeneous Disjunctions and Kim's Challenge
Fodor and Putnam deny that multiply realizable upper level properties
can be identified with or defined in terms of lower level properties. Rigidity
cannot be characterized in terms of a lattice structure of the sort that
we find in many rigid materials, since an amorphous structure such as glass
can also be rigid. Pain and thought may be similarly multiply realizable.
Let us suppose so. But if that is so, can't pain be identified with or
defined in terms of the disjunction of all of its nomically possible
realizations? Putnam (1967) said that this possibility "does not have
to be taken seriously". But Kim has raised questions that lead me
at least to take it very seriously. The rest of this paper is concerned
with this issue.
Consider the disjunctive property whose disjuncts are every physico-chemical
property that could, compatibly with the laws of nature, realize pain.
Pain is nomically equivalent to that disjunction in that the two
are coextensive in all possible worlds compatible with the laws of nature.
So why isn't pain identical to that disjunction? Or at least, why can't
we "define" 'pain' in terms of that disjunction for the purposes
of reducing psychology to physics and chemistry? This is the challenge
that Kim raises for the anti-reductionists.
We can get clearer idea of what it is for pain to be nomically equivalent
to a heterogeneous physico-chemical disjunction by considering the objection
that nothing could be nomically coextensive with a heterogeneous disjunction
because heterogeneous disjunctions have no place in laws. This objection
is a red herring. To see why, we must distinguish between two grades of
nomic necessity. The strong grade is nomic necessity as a matter of law.
For example, electrical and thermal conductivity are coextensive as a matter
of law, the Wiedemann-Franz law. The weaker kind of nomic necessity attaches
to anything that is true in all possible worlds that are compatible with
laws of nature. (We don't have to answer the question whether there are
more possible worlds compatible with the laws of physics than with all
the laws of nature to understand nomic equivalence.) Consider certain consequences
of laws. Suppose it is a law that all metals expand when heated. Then it
is nomically necessary that all metals either have the property of expanding
when heated or are made of green cheese. Because of the heterogeneous disjunction--expands
when heated or is made of green cheese--this claim is perhaps not a law,
but the heterogeneous disjunction does not preclude its being nomically
necessary. However we decide to use the word 'law', the point is that there
is a kind of nomic necessity that is not allergic to heterogeneous disjunction,
so the attempt to appeal to intuitions about laws to rule out the nomic
equivalence of pain with a heterogeneous disjunction won't fly.
It is worth noting that consequences of laws are often very unlike stereotypical
laws, yet are nomic necessities in good standing. Another example is "apparatus
necessities" (Block, 1994): consequences of laws keyed to descriptions
of a specific apparatus. Thus consider a setup in which the insertion of
some coins in a machine causes a box of candy to emerge. Suppose we could
completely describe the machine, the insertion and the candy emergence
in terms of the motions and masses of all the particles therein. Then the
description of the input and the machine, together with the appropriate
laws of physics, would entail the description of the output, revealing
that what happened was a nomic necessity (idealizing away from quantum
effects and external perturbations). Any object (machine plus inserted
coins) with that elementary particle constitution has to evolve
in that way, yielding the box of candy.
In terms of this distinction between laws and mere nomic necessities,
or, if you like, between two grades of nomic necessities, then, all Kim
requires is nomic equivalence in the weaker of the two senses, and that
is the way that I will be using the term 'nomic necessity' (and 'nomic
equivalence') here. (Incidentally, nomic necessities in the sense used
here do not include by-products of the initial conditions of the universe.
Nomic necessities are true in all possible worlds compatible with laws
of nature whatever the initial conditions.)
Now back to Kim's challenge. There is a disjunction of physico-chemical
properties that can, compatibly with the laws of nature, realize pain.
The coextension of pain with that disjunctive property is nomically necessary
(in the weak sense). So can this nomic equivalence serve to reduce pain
to the physico-chemical disjunction? Another lame answer is: no, because
the disjunction is infinite. But why is an infinite disjunction incompatible
with the aims of reduction? And even if infinite disjunctions are incompatible
with the aims of reduction, how do we know that the disjunction is infinite?
The universe is now thought to be Riemannian and if the curvature is constant
and positive (unknown at present), it is finite in space-time, so for all
we know the disjunction may be finite too. The anti-reductionist should
not try to base his position on a speculative empirical claim. But the
more important response is the question: why is a nomic necessity between
pain and an infinite disjunction incompatible with the aims of reduction?
Kim's challenge is not met by simply invoking infinity.
Fodor responds to the puzzle I am focusing on by, in effect, adding
a condition to Nagel's conception of reduction, namely that the inter-level
definitions or bridge principles connect kinds to kinds.
And he assumes that a heterogeneous disjunction is not a kind. But he does
not say why this nomic equivalence is no good for reduction.
Before I pursue these questions further, let me just say a word about
heterogeneity. The disjunction of all nomologically possible realizations
of, say, pain, is said by Kim to be a heterogeneous disjunction. But, one
might object, it is not totally heterogeneous, since the disjuncts resemble
one another at least in that they are all realizations of pain. I believe
that Kim thinks of this resemblance as highly superficial, along the lines
of saying dormitive substances resemble one another in that they cause
sleep. I will return to this issue in the second half of the paper, but
for now I will go along with thinking of these disjunctions as heterogeneous.3
Explanation
We might hope for some illumination on heterogeneous disjunctions by
considering the explanation condition on reduction. Laws of the
reducing theory together with "bridge" laws or definitions are
supposed to explain the laws of the reduced theory. This condition is often
ignored in the debate over multiple realizability because of the widespread
positivist assumption that explanation is just deduction. If the terms
of the upper level theory are all definable in lower level terms, explanation
of the upper level laws is said to be trivial. The upper level laws can
be deduced from the lower level theory plus definitions, and if the lower
level theory isn't rich enough, the "images" of the upper level
laws can simply be added to the lower level theory. As images of laws,
they will be nomically necessary. But if one has to do psychology
to discover basic laws of physics, the deduction of those laws of
psychology from their images in physics won't be as explanatory as one
might wish.
So let us ask: Will heterogeneous disjunctions at the lower level suffice
for explaining upper level laws? Consider an upper level law, U1=>U2.
(I leave out quantification for simplicity.) U1 is realized
by a heterogeneous disjunction, L1 or L1*--nothing
else can realize U1 (let's suppose). And U2 is realized
by another heterogeneous disjunction, L2 or L2*.
Now suppose there are two sorts of cases in which the upper level law holds,
the starred and unstarred cases, and we can explain each case of
U1=>U2 via appeal to the lower level. That is,
there is a lower level law L1=>L2 and another
lower level law L1*=>L2*. Each case of U1=>U2
is explained by one of these laws.
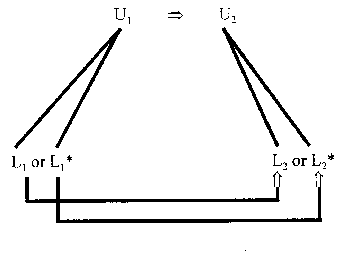
Figure 1: U1 is realized by a heterogeneous
disjunction, L1 or L1*; U2 is realized
by another heterogeneous disjunction, L2 or L2*.
There is a lower level law L1=>L2 and another
lower level law L1* L2*. Each case of U1=>U2
is explained by one of these laws.
Are the properties U1 and U2 and the law U1=>U2
thereby reduced or not? Of course, there is all the difference in
the world between a reduction to a heterogeneous disjunction and a reduction
to a single property that gives a uniform explanation of all cases. But
that doesn't show that there is no reduction to a heterogeneous disjunction.
In one sense of 'reduction' yes, there is a reduction, and in another sense
no, there is not. In one sense of 'reduction', if you have explained each
implementation of the law, you have reduced the law. But if the question
at hand is just a matter of how one decides to use the word 'reduction',
it is of little interest. Philosophers sometimes analyze our ordinary concepts
such as knowledge, belief, etc., and these analyses have a point because
our everyday concepts are of interest to us. But there is much less interest
in analyzing technical philosophical concepts. We should use whatever technical
concepts do the jobs we want done. I mentioned that Fodor adds the condition
to Nagel's characterization of reduction that bridge principles connect
kinds to kinds. If we are to accept this revision, it will not be as a
stipulation about the words 'reduction' and 'kind', but as a way of codifying
the idea that bridge principles that link kinds to heterogeneous disjunctions
are importantly defective. But we have yet to find a persuasive rationale
for this idea. The upshot of the remarks of the last few paragraphs is
that it is not obvious how to find an answer in the requirement of explanatory
adequacy.
Fodor (1974) hints at a proposal: what's wrong with bridge principles
that connect kinds to heterogeneous disjunctions is that the disjunctions
do not have their kind-hood independently certified. We should not
accept the nomic equivalence of upper level kind U1 with a lower
level disjunction L1 or L1* as a bridge principle
unless the disjunction appears in laws at its own level. But this condition
has no teeth. If U1=>U2is a law, and if
U1 is nomically equivalent to L1 or L1*
and U2 is nomically equivalent to L2 or L2*,
then [L1 or L1*]=>[L2 or L2*]
is just as nomically necessary as is U1=>U2. If
the lower level theory does not contain this nomic necessity, it can just
be added, as just noted, and the upper level law is reducible to the lower
level science, so supplemented, in one sense of 'reduction'. Of course,
Fodor's condition rules out the reduction if [L1 or L1*]=>[L2
or L2*] is not a law. But the question of whether this
nomic necessity is a law amounts to the question as to whether the disjunctions
([L1 or L1*], [L2 or L2*])
are kinds, and that is the very question to which we do not yet
have an answer. And even if we accept that the disjunctions are not kinds
and the nomic necessity involving them is not a law, we still lack an answer
to the question of why that ought to block reduction.
Kim's Proposal
The place we are at in the dialectic is this: Fodor blocks the use of
a bridge definition connecting pain to the physico-chemical disjunction
with which it is nomically equivalent by laying down two conditions on
reductions: First, bridge definitions connect kinds to kinds and second,
heterogeneous disjunctions are not kinds. But we have yet to see a justification
of these ideas.
Kim now enters the fray with a proposal: kinds are projectible properties.
He shows that this proposal has a very important merit in light of Fodor's
suggestion about kinds, namely that heterogeneous disjunctions are not
projectible and therefor they are not kinds. (A and B are projectible if
finding of an A that it is a B gives one some--even if very small--justification
for believing that the next A is a B.)
Consider the putative law that people who have (rheumatoid) arthritis
are helped by (that is, their symptoms are meliorated by) Ibuprofen. Suppose
that this is a well confirmed law. We have 50,000 recorded cases of people
who have the disease and who are helped by the drug, and no contrary cases.
Now pick another disease at random, say lupus, and consider the putative
law that people who have either arthritis or lupus are helped by Ibuprofen.
This putative law has a heterogeneous disjunctive property (arthritis or
lupus) in its antecedent. Does that prevent it from being well confirmed
by the same data that confirmed the original law? Each person who has arthritis
also has either arthritis or lupus. So if the disjunction is projectible,
then each datum that confirms the original law also confirms the disjunctive
law. Now we have the principle that if P is "well" confirmed
and P entails Q, then the evidence that "well" confirms P also
confirms (though perhaps not well) Q. (The need for the 'well' is discussed
in the footnote at the end of this paragraph.) But the claim that people
who have arthritis or lupus are helped by Ibuprofen is equivalent to the
conjunction of the following two laws:
And if the the law with the disjunctive antecedent is well confirmed
by the data that confirms the first of these laws, then the second is confirmed
by the same data. But we have no information about lupus in this data base
at all, so the assumption that the disjunction is projectible leads to
a ridiculous result. Conclusion: the heterogeneous disjunction is unprojectible.4
One question one might have about Kim's proposal is what notion of projectibility
he might have in mind. The usual notion of projectibilty may be too epistemic
to bear the metaphysical weight that the notion of a kind is supposed to
bear. This idea is bolstered by attention to Kim's argument, to which we
now turn.
Kim's Argument I
Here is the first part of Kim's argument. Pain is nomically coextensive
with a heterogenous physico-chemical disjunction. Therefor either both
pain and the disjunction are kinds, or neither pain nor the disjunction
are kinds. Why? Because the kinds are the projectible properties, and one
of two nomically equivalent properties is projectible if and only if the
other is.
But wait! Why is it that nomically equivalent properties must be both
projectible or both not? Here we see again that the usual notion of projectibility
is not what Kim needs, for on the usual notion having to do with justified
belief, we could be justified in supposing that something will have one
of two nomically equivalent properties without being justified in supposing
it will have the other. For one might not know about the nomic equivalence.
The notion of projectibility that Kim needs is what one might call objective
projectibility, which hinges on a notion of objective evidential
support, whether or not anyone knows about it. The idea would be that if
there is a certain degree of evidential support for the obtaining of one
property, the same degree of objective support obtains for any nomically
equivalent property whether or not anyone knows about it. In what follows,
I will assume that some such notion is available. (An alternative line
of thought, which I will not pursue, would be to take all of projectibility,
nomicity, reduction and kindhood to be fundamentally epistemic.)
Now back to the argument. Both pain and the heterogeneous disjunction
that is nomically equivalent to it are kinds or neither are. If both are
kinds, then the multiple realizability argument against reductionism is
no good. For the bridge law that associates pain with the disjunction links
a kind to a kind, thereby disarming the Fodor-Putnam objection to the reductionist
claim that pain is reducible to the disjunction. If the second alternative
is right, if neither is a kind, then in particular pain (and thought) is
not a kind and there is no genuine science of pain or thought. The power
of Kim's argument is that reductionism beats the Many Levels view and the
multiple realizability argument either way. If there are general
psychological kinds, they may be reducible despite the multiple realizability
argument. And if there aren't any general psychological kinds, reductionism
wins in another way. For even if there are no general psychological
kinds, there can nonetheless be restricted psychological kinds that are
not multiply realizable with respect to lower level science. Pain in general
and thought in general are multiply realizable. If that makes them non-kinds,
perhaps human pain or human thought is not multiply realizable, or if not,
Ned-pain or Ned-thought or Ned-pain-now. And so there is room for these
restricted kinds to be reducible to physics and chemistry.
Kim's Argument II
Thus far we have seen a dilemma for the anti-reductionist: both pain
and its disjunctive nomic equivalent are kinds or both are non-kinds. If
the former, there is no multiple realization and reductionism avoids the
multiple realization argument; if the latter, pain and other mental properties
are not kinds at all and there is no science of them as such. Though Kim
is inclined to emphasize the dilemma, he has a powerful argument in favor
of the latter position--that there are no special science kinds as such,
that is that there are no multiply realizable special science kinds, and
the only special science kinds there are are those that are reducible to
the physics and chemistry of the specific realizations. Pain is not a kind;
human pain probably is, but only because it is reducible to a human physical
kind. The argument is simple: the reasoning illustrated by the arthritis
and lupus example establishes that heterogeneous disjunctions are not projectible
and therefor not kinds. But if they are not kinds, then neither are the
special science properties like pain and thought that are nomically equivalent
to them. The upshot is that properties distinctive of psychology, economics
and biology that are multiply realizable, being nomologically equivalent
to heterogeneous physico-chemical disjunctions, are not kinds at all. There
are no genuine multiply realizable sciences.
Kim illustrates the point with this example: consider the claim that
jade is green. Suppose we send out our assistant for samples of jade and
we find that all are green. Is the claim that jade is green well confirmed?
No, for perhaps all the samples the assistant has brought in are jadeite.
(There are two minerals that are classified as jade: jadeite and nephrite.)
On that basis we should not expect that the next sample of jade that is
nephrite will be green. So "Jade is green" is not a law. And
the reason is that jade is not a kind (that is, not projectible) but rather
a heterogeneous disjunction of two kinds, nephrite and jadeite.
In his paper in this volume, Jerry Fodor notes that jade is not the
concept of a certain set of superficial properties like appearance and
malleability. If one could transform glass so as to look and act like jade,
that wouldn't make it jade. But this claim does not motivate any objection
to Kim. Kim's use of the example depends mainly on the fact that jade is
a heterogeneous disjunction, and Fodor's point does not challenge that.
Second, if we find some previously unknown kind of stone that has all the
superficial properties of jade, we might well count it as a third type
of jade, even if no samples of it had been classified as jade before. It
would be synthetic jade not artificial jade. Glass may be ruled out because
it is not a stone or because it is a substance that has been classified
in the past as non-jade.
Fodor makes a distinction between an open and a closed disjunction.
Jade is a closed disjunction because (according to Fodor) only substances
that are jade in the actual world (jadeite and nephrite, as far as we know)
can be jade in any possible world. Realizers of pain are an open disjunction
because even if there are no actual silicon pains, there are possible silicon
pains. Fodor thinks that Kim's argument depends on ignoring this distinction,
but it seems rather that Kim's argument actually gains power from
the open/closed distinction. Kim's argument is could be put this way: since
that open disjunction is nomically equivalent to pain, pain is just as
non-projectible and non-kind-like as that open disjunction. The gain in
power derives from the plausible unprojectibility of an open disjunction.
For another illustration of Kim's position, consider dormitivity, the
property of a substance that consists in its having some other property
such that if the substance is ingested, that other property causes the
ingester to sleep. Dormitivity is a second order property in that
it is defined as the possession of some other property (usually a first
order property) that has a certain causal role. The notion of a second
order property is a slight generalization of the notion of a functional
property that has played such a large role in the establishment of the
anti-reductionist consensus. (A functional property is the possession of
some property that has a certain causal role with respect to inputs, outputs
and other properties that also mediate between inputs and outputs.) There
is a simple account of the notion of realization in terms of the
notion of a second order property. The realizations of dormitivity are
just the first order properties that actually cause sleep.5
Secobarbitol and diazepam are chemically different substances that both
cause sleep (in different ways), and they are therefor realizations of
dormitivity. For simplicity, let's suppose that secobarbitol and diazepam
are the only nomologically possible realizations of dormitivity. So either
dormitivity is a kind and is reducible to the heterogeneous disjunction
of secobarbitol and diazepam. Or the disjunction isn't a kind and neither
is dormitivity.
Kim's argument commits him to the latter option. Suppose we ask our
assistant to bring us dormitive substances. We test each one in our lab
and find that they are all carcinogenic. Should we conclude that the next
dormitive substance that the assistant brings to us is likely to be carcinogenic
too? In other words, is dormitivity projectible? Kim's line of thought
dictates no. For suppose that we find out that all the samples of dormitive
substances that our assistant has brought to us and that we have tested
are samples of secobarbitol but the next dormitive substance is diazepam.
The reasoning just mentioned dictates that we cannot project carcinogenicity
from secobarbitol to diazepam. Dormitivity is not a kind because it is
not projectible. The basis of kinds is similarity and that is precisely
what heterogenous disjunctions lack.
The upshot is that the supposed kinds of psychology and other multiply
realizable special sciences are not kinds at all. Kim asks us to consider
a possible law:
"Sharp pains administered at random intervals cause anxiety reactions".
Suppose this generalization has been well confirmed for humans. Should
we expect on that basis that it will hold also for Martians whose
psychology is implemented (we assume) by a vastly different physical mechanism?...The
reason the law is true for humans is due to the way the human brain is
"wired"; the Martians have a brain with a different wiring plan,
and we certainly should not expect the regularity to hold for them just
because it does for humans. ..."Pains cause anxiety reactions"
may turn out to possess no more unity as a scientific law than does "Jade
is green." (Kim, 1992, p. 16)
The analogy between dormitivity and pain is apt from Kim's point of
view. His arguments point towards the conclusion that there is no more
of a science of pain than there is of dormitivity. In both cases, the real
scientific kinds are those of the realizations, the chemicals that cause
sleep in the case of dormitivity and the specific neural structures of
specific pain-feeling organisms in the case of pain. What is common to
pains in virtue of which they are pains (a question I pressed in Block,
1980b)? According to Kim, the answer is conceptual: the concept of pain
is second order, the concept of a state of having some other property that
has a certain role. Similarly, what is common to dormitive substances in
virtue of which they are dormitive is simply that they fit the concept
of dormitivity, that is that they cause sleep. Fodor notes that "What
makes Wheaties the breakfast of champions?" (a question that used
to appear in advertising) has two types of answers. There is a conceptual
answer: it is eaten by lots of champions. And there is a scientific answer
which you'll have to ask a nutritionist about, perhaps that it has just
the right balance of vitamins, minerals and insect parts. Kim's answer
to "What do pains have in common in virtue of which they are pains?"
is an answer of the first sort. Pain has an a priori conceptual analysis
as a second order property, as does dormitivity. And there is no answer
of the second sort.
The anti-reductionist may be tempted to make a simple retort: "Look,
there are special sciences, as a glance at any economics or cognitive
science journal shows. So any argument that there aren't any is badly off
base." But Kim's point is not so easily silenced. Of course, in some
sense there are special sciences. But there is some latitude in interpreting
what it is that they are about. The upshot of Kim's argument is that real
scientific enterprises do not have multiply realizable domains. In Kim's
view psychologists are real scientists, but they study human psychology
which is a science precisely because it is not multiply realizable. Presumably,
he will say that geology is the science of specific physical structures;
to the extent that Earthian geology is similar to Jupiterian geology, that
is because they intersect in various ways via branches of physics such
as hydrodynamics. (Jupiter is a congery of gasses, some of which act like
liquid metals. And the earth's core is molten.) This line is not at all
plausible for computer science and economics. No doubt he will say that
computer science is a branch of mathematics, not the science of any multiply
realizable physical structure. And other special sciences are combinations
of mathematics and structure restricted sciences like human psychology.
Economics would be a good candidate for this kind of analysis.
Hartry Field has suggested that the reductionist can be refuted by examples
of properties within physics. The property of being a rigid body plays
a role in laws of mechanics-there are lawlike relations between rigidity,
center of mass, moment of inertia and angular momentum, for example. So
rigidity is a kind. Further, Field arrgues that it is a second order property,
the property of being subject to constraining forces (the first order properties)
that keep the parts of the rigid object at constant relative distances
and that do no net work in any motion compatible with the constraints.
And it is multiply realizable because different rigid substances (e.g.
amorphous rigid materials like glass and crystalline rigid materials like
ice) have different constraining forces. Further, rigidity is not reducible
to anything first order. No one would suppose that rigidity could be reduced
to a vast disjunction of types of rigid bodies. In sum, we have a clear
counterexample to Kim's argument.
I think that Kim has a straightforward reply: he should distinguish
between ideal rigidity and real rigidity. Ideal rigidity can be
defined purely geometrically: All points in a rigid body maintain constant
relative distances. Ideal rigidity is not second order and it is not multiply
realizable. Real rigidity is the property that Field defines. It is second
order and multiply realizable, but there is a real issue as to whether
there are any general laws about it. The need for quantification over forces
comes into the definition of real rigidity because there are conditions
in which genuine rigid objects lose their constant interpoint distances,
e.g. inside a black hole. But it would seem that the general laws concern
ideal rigidity. For example, the center of mass of a rigid body obeys the
2nd Law of Newtonian Mechanics, it maintains a constant velocity
(which may be zero). If there are any laws about real rigidity, they concern
the conditions in which it breaks down, but those will be different
for different rigid substances.
You may wonder why ideal rigidity isn't multiply realizable. You may
ask: aren't glass, ice, etc. all realizations of it? The problem with this
objection is that glass, ice, etc., don't so much realize the property
of rigidity as have it. One common notion of realization mentioned
earlier appeals to parallel families of properties. The relations among
temperature, pressure, entropy, etc are mirrored by relations among mean
molecular kinetic energy, momentum exchange, etc, and the latter family
provide a mechanism for explaining the relations among the former. That
is what makes the latter properties realize the former, or anyway it is
closely connected to what makes for this realization. Or to take another
type of case, we can construct a multiplier from a system containing an
adder, a decrementer-by-1 and a checker-for-zero. These items can be realized
in one machine by one set of circuits and in another machine by another
set of circuits. In both cases, we have a family of circuit properties
that provide a mechanism for explaining how the adder, decrementer, etc
interact to do the job. But it is hard to see a similar story for rigidity.
Properties that are at the same level as rigidity include center of mass
and moment of inertia. But if we want to explain the machinery by which
the center of mass of a piece of rigid glass interacts in a certain way
with moment of inertia, etc, we appeal to the same sorts of properties
of mechanics, only applied to smaller things. There does not seem to be
a "micro-family" of the right sort.
In my rendition of Kim's argument, I have left out one very important
aspect, considerations of causality. Kim holds that kinds are causally
individuated, that is that objects and events fall under a kind to the
extent that they have similar causal powers. This idea is linked to the
just mentioned notion of kinds as projectible by the common connection
of projectibility and causation to laws. Kim argues that all causal powers,
and hence all kinds are physical causal powers and that there are no causal
powers at the level of multiply realizable properties. The property of
pain is no more causally efficacious than the property of being a table.
But human pain (or Ned pain if human pain is multiply realizable, or Ned
pain now if Ned pain is multiply realizable) is identical to a physical
kind, according to Kim, and is therefore causally efficacious. (Kim calls
this view multiple type physicalism.) I won't summarize Kim's argument
that multiply realizable properties are not causal kinds. What will be
relevant later is only the fact that Kim assimilates the causal kinds just
mentioned to the projectible kinds I have been talking about. The link,
as I said is that both causation and projectibility are to be understood
in terms of law.
Recap
Kim's radical challenge to the anti-reductionist consensus has three
parts (leaving out causation):
- If property M (say a mental property) is nomically coextensive with
a heterogeneous disjunction of physico-chemical properties, then either
both or neither are kinds.
- Heterogeneous disjunctions are not kinds because they are not (objectively)
projectible; so M, being nomically equivalent to a heterogeneous disjunction,
is not a kind. So there is no completely general science of psychology,
that is, no science that covers all the heterogeneous realizations of human
functional organization, both minds and machines. The sciences of the mental
are the sciences of the realizations themselves.
- The anti-reductionists think that there are mental kinds which are
second order, and there is a science of them. We can see why they think
that and why it is wrong by noting that:
- There is something second order that applies generally, namely second
order mental concepts
- There are structure-restricted sciences of the mental kinds that are
not multiply realizable.
The Disney Principle and Forces of Convergence
It is important to note just how radical Kim's position is. It is very
tempting to believe that in addition to the concept of pain, there
is a property of pain, and that property is multiply realizable.
Creatures with different physiologies might nonetheless all share that
property, pain. But according to Kim, there is no serious property in common
to pain-feeling organisms. What they share is just a matter of falling
under the concept of pain.
In my view, this objection shows that Kim cannot in general be right.
But this conviction is based on my view that pain-and other conscious states-have
no functional conceptual analysis. (My view is that if pain is a
functional state, it is what I call a psychofunctional state, a
state captured by empirical functional analysis.) And I do not wish my
reply to Kim to depend on controversial ideas about consciousness. So in
what follows I will ignore consciousness, keying my reply to special science
properties that are shared among a variety of special sciences, some of
which do not traffic in consciousness.
Kim has produced an impressive challenge to the anti-reductionist consensus,
one that in my view requires some important adjustments to that consensus.
However, I still favor a modest version of the Many Levels view according
to which psychology and other special sciences whose kinds are multiply
realizable are autonomous sciences with genuine kinds that are not on the
whole reducible to a lower level. One way of leading into my disagreement
with Kim is to note that these special science kinds are typically not
nomically coextensive with completely heterogeneous disjunctions
of physico-chemical properties.
In Walt Disney movies, teacups think and talk, but in the real world,
anything that can do those things needs more structure than a teacup. We
might call this the Disney Principle: that laws of nature impose constraints
on ways of making something that satisfies a certain description. There
may be many ways of making such a thing, but not just any old structure
will do. It is easy to be mesmerized by the vast variety of different possible
realizations of a simple computational structure, say that of an and
gate, which can be made of cats, mice and cheese (Block, 1995) as well
as mechanical or electronic components. But the vast variety might be cut
down to very few when the function involved is mental, like thinking, for
example, and even when there are many realizations, laws of nature may
impose impressive constraints.
Of course we can only guess what constraints are imposed on realizations
of mental properties. I've already mentioned one trivial constraint: a
thinker requires a structure different from that of a teacup. Here is a
guess as to a more general and slightly less trivial constraint: a thinking
thing cannot be composed entirely of a liquid or a gas. This is a shot
in the dark, but a plausible one based on current theories of either the
classical or connectionist variety: both liquids and gases seem too amorphous
to support the kind of structure that seems to be required for thought
processes according to current theories.6
Of course, the plausibility of such a suggestion may rest on ignorance
or lack of imagination. But even if we can have little confidence in any
specific guess, still it would be amazing if laws of nature imposed no
constraints at all on what can think or be conscious. The reductionist
may say that cutting down on the possible realizations still allows heterogeneous
realizations, but this idea ignores the fact that constraints impose similarities.
For example, if my speculation is right, all thinkers are similar in not
being totally gaseous or totally liquid. This may seem not a very interesting
similarity, but it is only a proxy for constraints that may some day be
discovered.
These hypothetical constraints concern the the physical structure of
realizations of thinking, but there might also be constraints at other
levels. I mentioned that current theories of thinking fall into two paradigms,
classical and connectionist. Perhaps thinkers can be made that fit both
of these programs, but it may be that there are no other ways to make a
thinker. The classical paradigm follows the model of the digital computer:
explicitly represented rules that are applied to inputs via hardware that
embodies much simpler implicit rules. The connectionist paradigm is associationist,
involving vast arrays of nodes and interconnections; the nodes and connections
have modifiable weights that control the extent to which they pass on activation,
and these weights change according to the past activations they have participated
in. There are no explicit rules. The essence of both of these paradigms
is to be found at a level of abstraction far above that of physics and
chemistry. If thinkers can only be constructed according to those paradigms,
laws of nature impose very abstract constraints.
A second factor that points towards homogeneity and away from heterogeneity
is that there are forces at work that can be expected to produce
similarities. The first such force that comes to mind is natural selection.
(After writing this, I read Papineau, 1993, which makes a similar point.)
A famous example is the eye, a structure that has evolved more than once.
(But not as often as once thought). Further, learning often produces the
same mental structures by different means. The understanding of fractions,
for example, is inculcated anew, in different ways, in each generation
of elementary school students. Another force that produces similarities
is conscious design. Pens tend to have similar properties despite a great
deal of difference in materials and principles of operation, e.g. they
don't dissolve in ink. And there are mixed mechanisms. For example, economies
are constantly being tinkered with by governments. When catastrophe seems
to loom, often changes are made. If the changes don't work, the government
makes more changes. This is a kind of combination of (non-Darwinian) evolution
and design.
Such forces acting by themselves, however, are unlikely to produce much
in the way of deep scientific similarities of the sort that the experimental
special sciences investigate. To the extent that evolution and design produce
similarities all by themselves, they are likely to be relatively
superficial. (A type of exception will be mentioned later.) There are no
deep scientific laws of pens. If there are any surprising uniformities
among pens, it will only be because there are some hidden consequences
of rational design for certain purposes. Natural selection doesn't care
about the deep scientific nature of, e.g. a language aquisition device
but only that it do the job.
The power of natural selection to produce similarities in realizations
derives from the fact that the two factors just mentioned interact, for
the forces that create complex functions can only move in certain channels,
the ones provided by the restrictions mentioned in the Disney Principle.
In the case of simple functions such as that of a pen, one can expect little
chanelling. But in the case of a more complex function such as that of
a computer, one expects-and finds-more. Further, if my speculation is right
that a thinker can only be constructed according to classical or connectionist
principles, then forces of design or selection will have to move in one
of these two channels to make a thinker. Evolution, learning and the like
impose similarities at the more superficial levels. We expect evolutionarily
unrelated eyes to be similar in at least some general principles of operation,
for they have to solve the same problem. Light has to be conveyed to some
light-sensitive surface while preserving its informational content. But
evolution and learning do not impose similarities in realization.. The
Disney Principle, by contrast, indicates similarities at all levels. There
are constraints on how one can make an eye at the "design" level,
but there are also constraints imposed by the fact that only some materials
are transparent enough to transmit light without destroying much information.
An eye requires some such material at least in the part that points at
the world. So there are reasons to expect less than total heterogeneity
at both the design and realization levels. Since evolution enforces similarity
only at the design level, we should expect more variation at the levels
of realization than at the design level. And this is why we expect multiple
realization.
If there are distinct constraints at different levels, it is no surprise
that as Putnam (1975) noted, different idealizations are appropriate at
different levels. From the point of view of a programming theorist, the
flip-flops in computers are all-or-nothing devices. But from the point
of view of someone who studies those devices in somewhat greater electronic
detail, they are continuous. E.g. a flip-flop may have two states, a 4
volt potential for 'off' and a 7 volt potential for 'on'. And in changing
values, it will move through intermediate values. But a still deeper level
sees these devices as digital again, since the charge is carried in packets.
In the light of these points, consider, Kim's putative law "Sharp
pains administered at random times cause anxiety reactions. First, any
creatures who are the products of evolution of the sort that has taken
place on earth can be expected to have the kinds of relations among mental
states that are favored by evolution. If there is an evolutionarily inculcated
relation between random sharp pains and anxiety reactions in us, then there
is some reason to expect it in any other evolved intelligent creature
capable of pains and anxiety reactions. Further, given that there may be
substantial restrictions on ways of making a pain-feeling organism, we
shouldn't be surprised if the same relation applies to Martians. A better
example of the sort of properties that are selected for in the case of
pain (better than causing anxiety, that is) would be the relation between
pain and distraction. A moment's thought suggests that the tendency of
pain to distract serves the function of making sure the pain is a focus
of attention, thereby raising the probability of efforts to get rid of
its source.
I said a moment's thought would lead us to expect naturally evolved
creatures who have pain to be distracted by it. But another moment's thought
should lead us to doubt this claim. After all, distraction can be counterproductive.
A human with a sprained ankle who is being pursued by a bear would do well
to concentrate all her attention on escaping instead of dwelling on the
pain of the ankle. If one were designing a pain feeling creature, one might
want to make sure that the creature knows about her pains and that avoiding
pain is fairly high up on the creature's list of preferences, but if one
can do this without soaking up attention paid to the pain itself, so much
the better. Another reason to doubt that it is adaptive for pain to be
attention-grabbing is that we ourselves have pains that do not appear to
engage attention. People are forever changing the disposition of their
limbs (e.g. crossing and uncrossing legs) in response to discomfort without
any obvious use of attention. People who are unable to feel pain do not
do this and for that reason have medical problems. If one were designing
a body, one might want such things to happen automatically without using
up any attention.
The point I am making with this example is one that has been emphasized
by Lewontin and Gould. Adaptationist reasoning is cheap. One can come up
with a "just-so story" about why evolution should favor some
trait, but a bit more imagination will often yield an incompatible just-so
story. The fact is that for most traits, we are just not in a position
to know whether they are adaptations that have been selected for or mere
by-products of such adaptations, "spandrels" in the lingo of
Gould and Lewontin (1979). (The spandrels of San Marco in Venice seem to
be included in the design because of their beauty, but they are a by product
of design that puts a dome on a square base. 'Spandrel' can be glossed
as "by-product".)
The upshot is that we do not know which of the regularities that exist
in human mental life are specifically selected for (and thus could be expected
in other evolved creatures with the relevant mental states) or are spandrels.
Perhaps many of the regularities are spandrels. This is where the Disney
Principle comes in, for from the point of view of (my use of) the Disney
Principle, the distinction between adaptation and spandrel is irrelevant.
Consider the eye. On the basis of evolution considered in isolation, there
would be little reason to expect deep scientific similarities among evolutionarily
unrelated eyes. If evolution wants an eye that has the same function as
ours, why should it also make it scientifically like ours? But the Disney
Principle tells us that there are channels in which evolution must move,
for there are constraints on how one can make an eye given certain materials
in conditions of a certain range of temperatures, gravitational force,
etc. If these constraints mandate deep scientific similarities among eyes
of creatures that can exist in a certain range of conditions made out of
a certain range of materials, then those similarities are relevant to the
constitution of kinds whether or not the shared properties that constitute
the similarities are direct products of selection or spandrels.
How strong are the constraints imposed by the Disney Principle? We don't
know. And not knowing, we don't know how right or how wrong Kim's picture
of science is.
D Properties and Realization Properties
We can divide special science properties into the following two sorts:
those that are selected (whether selected for or not) and those that are
due to peculiarities of the realizations.
For an example of a property that is a peculiarity of a realization,
consider the fact that certain kinds of stimulations cause "ghosts"
of past pains. Stimulation of the nasal mucosa cause recreations of dental
pains. This phenomenon, "aerodontalgia", was discovered by U.S.
Air Force dentists who noted that pilots in unpressurized planes of World
War II (in which the sinus cavities expanded) reported pains that turned
out to be related to previous dental work in which local anesthetic had
not been used. (Nathan, 1985) It is most unlikely that this property of
pain was selected for, since the stimulations that elicit the ghosts of
the pain tend to require unusual conditions, often ones that require technology
that did not exist in our hunter-gatherer days. If this is just a by-product
of the physical realization of pain, then there will not be a high probability
that creatures whose pains are realized differently will have it unless
we share a common ancestor with them from which we both derive it. But
given that there no doubt are a limited number of ways of making a pain-feeling
organism, we cannot expect the likelihood even in this case to be zero.
Another example of this type is that if a hand is amputated, the amputee
later feels the sensation of the hand being touched when his cheek is touched.
Indeed, the feeling as of fingers of the hand all map neatly onto the cheek.
The subjects' sensations can be used to draw a hand on their cheeks. The
reason that the hand sensation "migrates" to the cheek is that
the hand receptors and the cheek receptors in the sensory cortex happen
to be adjacent. When the hand reception area stops receiving inputs, the
inputs from adjacent areas spread into the hand reception area.
Let us call the properties that are the product of channeled selection,
learning and design--in conjunction with the Disney Principle--"D
properties" ('D' for design and Disney), and let us call the properties
like aerodontalgia and the cheek/hand phenomenon "realization properties".
A dramatic example of a D property in psychology has recently been given
by Roger Shepard (1987, 1994). Suppose you eat a piece of fruit of a sort
that is new to you and you like it, so you reach into the fruit bowl for
another one like it. Given a range of choices, you will be more likely
to choose some items than others. All the data that Shepard has looked
at are consistent with a very strong result: the probability of generalization
approximates an exponential decay function of distance in an abstract psychological
space. Further, these spaces have one of two metrics, Euclidean or City
Block. The domains that Shepard has looked at include color perception
in pigeons and Morse code perception in people. Further, he has shown that
this sort of exponential curve is precisely what you would expect a good
engineer to build into a creature given some very simple assumptions about
the environment and needs of the creature. One of the assumptions, for
example, involves Bayesian inference. The generalization "Stimulus
generalization curves fit the Shepard description" is certainly projectible.
We would expect the next evolved creature to show the same curve. And we
would even expect an all-purpose artificial intelligent creature to show
it.
Though the generalization just mentioned is a deep scientific one, it
is not a model for all of experimental psychology. For as Shepard emphasizes,
it can be discovered by thought experimentation without much need for real
experimentation.
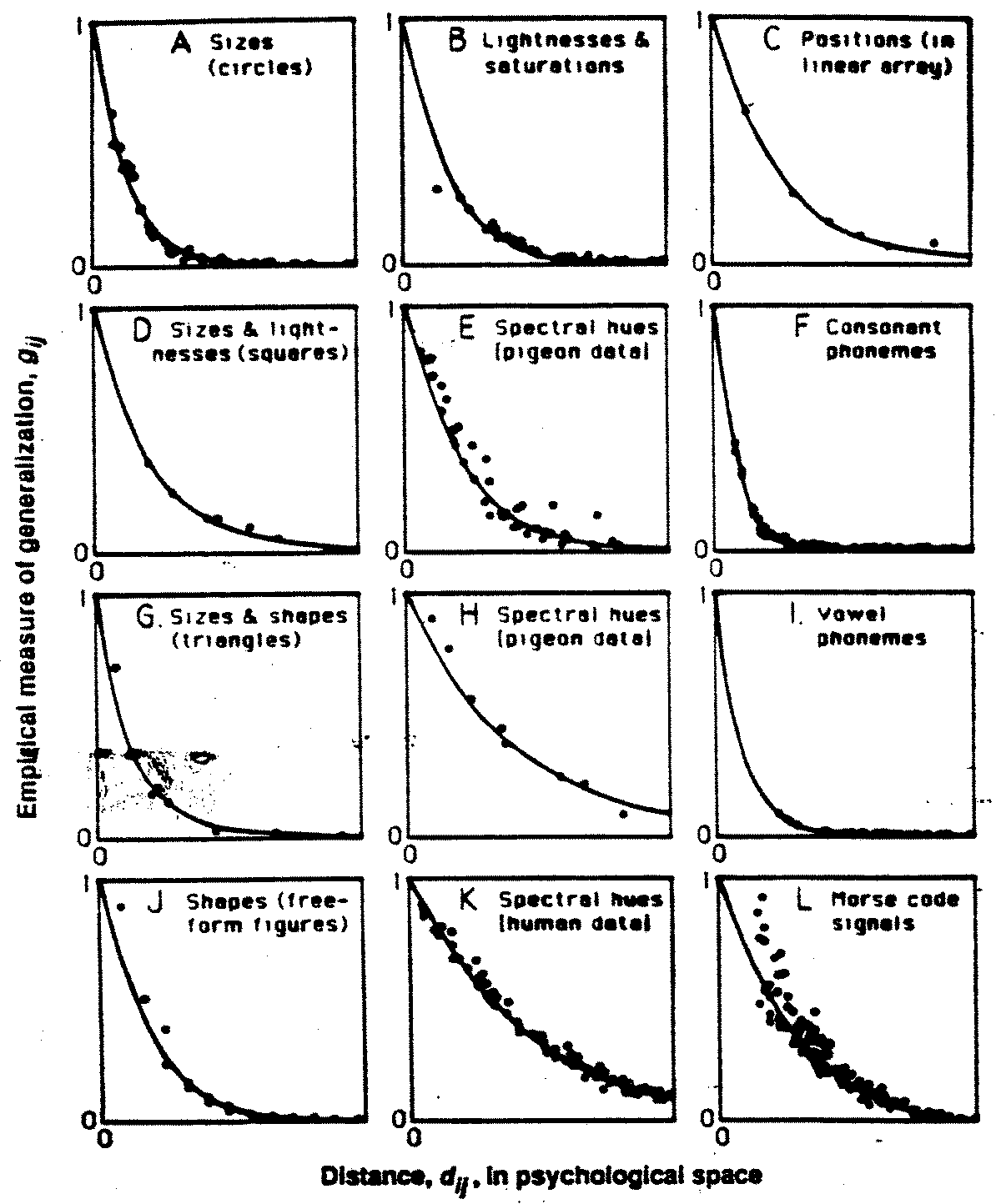
Figure 2: Twelve generalization gradients
from Shepard, 1987
The scorecard at this point is this:
- Kim is right about realization properties. Aerodontalgia and the hand/cheek
phenomenon depend on the realization of psychological phenomena. The science
of such psychological properties is not part of psychology. We wouldn't
expect such properties to generalize to pain-feeling creatures that are
not evolutionarily closely related to us.
- Kim is wrong about D properties. Stimulus generalization is a property
of perception that is common to creatures and perhaps machines that are
not very similar in realization of perceptual systems. Perception is both
a scientific kind and multiply realizable, even multiply realized.
It is important to note the difference between two theses:
- Perception is both a scientific kind and multiply realizable.
- There is a science of all possible perception.
Kim is probably right on 2 but wrong on 1. If there is a science of
all possible perception, it will be because nature imposes surprising constraints.
More likely, what is common to all perceivers in virtue of which they perceive
is that they fall under the concept of perception, as Kim would say. If
Fodor and Putnam would deny this, their view is unsupported. But that is
a very different matter from 1. We already know that Kim is wrong about
whether perception is both a scientific kind and multiply realizable.
Phenomena such as aerodontalgia and the hand/cheek phenomenon are a
partial
A general caution: As I mentioned earlier, I often simplify, talking
as if there is only one level of "realization". In the case of
psychology, I speak of "the" realization as being biology or
physiology. But of course, one can also consider whether biology itself
is multiply realizable in physics and chemistry.
Projectibility Again
In the light of these points, we should look back at the examples that
I used to illustrate Kim's point about projectibility. Kim says that "Jade
is green" is not projectible. But is it really true that a million
samples of green jadeite give us no reason at all to think that
the first sample of nephrite is green? The concept of jade is mainly a
concept of a certain appearance (according to my dictionary, being
pale green or white and used in carving or as a gemstone), and so jadeite
and nephrite, since they are both classed as jade, must share some appearance
properties. But no doubt there are some limits on ways of making things
that have those appearance properties,and we can expect those limits to
lead to other similarities, hence there will be some projection from jadeite
to nephrite. Of course I agree with Kim that the similarity in appearance
gives us little reason to expect any deep scientific similarity
between jadeite and nephrite.
I said that given that jadeite and nephrite have some superficial similarities
that gives us little reason to expect deep resemblances. Notice
that I did not say no reason. In fact, there are two reasons for
giving non-zero probability to deep resemblances. First, the Disney Principle:
surely there are some constraints on ways of making something that
looks and behaves in whatever ways define jade. (I doubt that you can make
such a thing out of water) A second point is that any real resemblance
makes another real resemblance a bit more likely.
(What's a real resemblance? Famously, any two things, x and y, share
a property, if only the property of being x or y. Of course, this raises
the issue of whether we can say what a real resemblance is without appealing
to the notion of a heterogeneous disjunction or the notion of projectibility
itself. Perhaps these notions are part of a family each member of which
can only be clarified in terms of others.)
These points about jade also apply to dormitivity. Given that secobarbitol
and diazepam resemble one another in one way, in causing sleep, that gives
us some reason to expect that they resemble one another in another real
property. Causing sleep seems a relatively superficial property, though
perhaps not as superficial as color. One can imagine stories according
to which the mere artificial production of sleep is carcinogenic, so there
is certainly some small reason to expect that if one is carcinogenic, then
so is the other. Of course, the degree of confirmation is small compared
to the confirmation given to the hypothesis that all secobarbitol is carcinogenic
from finding that some samples of secobarbitol are carcinogenic. Again,
one lesson even in these cases of no serious selection is that one can
expect different strengths of projectibility with respect to different
sorts of properties. A second lesson, is that given the Disney Principle,
there is a non-zero probability of similarity even in the realization properties.
I have been insisting on fractionating projectibility, arguing that
mental kinds project more to D features than to realization features. But
is this a way of avoiding the main question? Are the huge disjunctions
of physical properties that are nomically coextensive with money or thought,
kinds or not? The dilemma for the anti-reductionist, you will recall,
was that if they are kinds, then the multiple realizability argument
against reductionism founders, and if they aren't kinds, then the mental
properties such as thinking that are coextensive with the disjunctions
are not themselves kinds. So how do I avoid the dilemma? My answer has
two parts:
- I say that the issue of whether a property or a disjunction of properties
is a kind or not is relative. The relativity comes in with the question
of "Projectibility with respect to what type of property?" The
physical disjunction that is nomically coextensive with thought is a kind
relative to projection to D properties of psychology, but less so with
respect to projection to realization properties or with respect to D properties
of neurophysiology. For example, perceptual mechanisms are kinds with respect
to properties that have to do with stimulus generalization. But there will
be less reason to think of them as kinds with respect to the question of
whether or where a hand sensation will be felt if the hand is removed.
- A second point is that given that similarity comes in degrees and since
kindhood is based on similarity, kindhood comes in degrees too.
The upshot is that if pain is nomically equivalent to a physico-chemical
disjunction, then both pain and the disjunction will be kinds with respect
to some properties, but to a lesser degree with respect to others. Kinds
are relative and graded.
The point is partially supported by reasons to reject talk of projectibility
of properties altogether. As Davidson has argued, even grue
is projectible with respect to the right property. "All emeralds are
grue" is not projectible (i.e. it is not supported by finding a given
emerald to be grue). But suppose we define 'emerire' as discovered before
2000 and is an emerald, otherwise a sapphire. "All emerires are grue"
(arguably) is projectible. So there is reason to think that it is
hypotheses that are projectible, not properties. And if this is
right, the relativity of kinds can be derived in one step from the relativity
of projectibility.
The upshot if I am right is that most of the uses that both Fodor and
Kim make of the notion of a kind are off base. In the cases of interest,
the answer to whether a given property is a kind is almost always going
to be "Yes and no, to various degrees."
Kim and Fodor, despite very different points of view, agree that if
a mental property is nomically coextensive to a physico-chemical disjunction,
the disjunction will be heterogeneous and therefor not a kind. By contrast,
I say that such disjunctions can be expected not to be completely heterogeneous
even with respect to realization properties, and far from it with respect
to design properties.
Perception in evolved organisms is nomically coextensive with a physico-chemical
disjunction. Is evolved perception reducible to physics and chemistry or
not? Is the disjunction a kind? The answer, as I said, is yes and no, in
various degrees. The disjunction is a kind relative to psychological design
properties, but to a lesser extent relative to physico-chemical properties
themselves. One could define 'reduction' so as to require kinds relative
to the reducing science; or one could define 'reduction' so as to allow
kinds relative to design properties. The issue is terminological. If the
notion of a kind is the nub of the reduction issue, then there is no matter
of fact about reduction here. One relevant fact that is free of the
terms 'reduction' and 'kind' is that there are laws of evolved perception
in organisms that are relatively heterogeneous from the point of view of
physics and chemistry. In that respect, Fodor and Putnam are right.
In the scorecard given earlier, I said:
- Kim is right about realization properties like aerodontalgia and the
hand/cheek phenomenon. They don't project from one perceiver to another
- Kim is wrong about stimulus generalization. It does project from one
perceiver to another despite differences in realization.
- If Fodor and Putnam were committed to a science of all possible perception,
there is no reason to believe that they are right.
But now I have to revise the first two of these points. The fact that
realization properties like aerodontalgia don't project from one perceiver
to another doesn't show that perception or pain or any mental property
is a kind of a science that realizes psychology. And the fact that stimulus
generalization does project does not show that perception is a psychological
kind. The fact that kinds are relative and graded shows that there is something
wrong with the analytic apparatus common to Fodor and Kim. If talk of reduction
presupposes a non-relative non-graded notion of a kind, then there is no
matter of fact about reduction.
It is time to return briefly to causation. I mentioned earlier that
Kim assimilates causally efficacious kinds and projectible kinds, the link
being the notion of law which is key to both causation and projectibility.
One upshot of the ideas presented here is that we should perhaps distinguish
between causally efficacious kinds and projectible kinds. What is required
for a high degree of projectibility is that processes like selection and
design have connected properties that would not otherwise be connected.
Thus pen design has coupled cylindrical shape, having a point at one end
and allowing a fluid to come out the pointed end and other properties as
well. For certain sorts of properties (e.g. not dissolving in ink), one
can project pretty well from examined pens to unexamined pens. But does
that make being a pen a causally efficacious property? Why should the mere
grouping of properties together make the property of being a member of
that group a causally efficacious property? And how could causal efficacy
come in degrees? Once one agrees that the notion of kind is relative and
graded, unless one is prepared to see causation as relative and graded,
kinds will be poor candidates for the key to causation.7
Bibliography
Bealer, G. 1994 "Mental Properties" The Journal of Philosophy
XCI, 4, 185- 208
Blackburn, S. 1993 "Losing Your Mind: Physics, Identity and Folk
Burglar Prevention", Chapter 13 of Essays in Quasi-Realism,
Blackwell: Oxford
Block, N. 1980a Readings in Philosophy of Psychology, Vol 1 Harvard
University Press: Cambridge
Block, N. 1980b "What is Functionalism?" in Block 1980a, 171-184
Block, N. 1994 "Two Kinds of Laws", in C. MacDonald and G.
MacDonald, eds., The Philosophy of Psychology: Debates on Psychological
Explanation.Blackwell: Oxford, 1994.
Block, N. 1995. "The Mind as the Software of the Brain" in
An Invitation to Cognitive Science, second edition, edited by D.
Osherson, L. Gleitman, S. Kosslyn, E. Smith and S. Sternberg. MIT Press:
Cambridge
Churchland, P. S. 1986. Neurophilosophy, Cambridge: MIT Ch 7
Enç, B. 1983 "In Defence of the Identity Theory" Journal
of Philosophy 80, 279-298
Enç, B. 1986 "Essentialism without Individual Essences"
Causation, Kinds, Supervenience and Restricted Identities" In P. A.
French, et.al., eds. Midwest Studies in Philosophy XI Minneapolis:
University of Minnesota Press, 403-426
Fodor, J. A. 1965. "Explanation in Psychology" in Philosophy
in America, Max Black, ed., Muirhead Library of Philosophy
Fodor, J. A., 1974 "Special Sciences" Synthese 28,
97-115. Reprinted in Block 1980a
Gould, S. J. And Lewontin, R.C., 1979. "The Spandrels of San Marco
and the Panglossian Paradigm: A Critique of the Adaptationist Program".
Proceedings of the Royal Society, vol B205, 581-598.
Kim, J., 1972. "Phenomenal Properties, Psychophysical Laws and
the Identity Theory," Monist 56, no. 2, 177-192. Part of this
paper was reprinted in Block, 1980a under the title "Physicalism and
the Multiple Realizability of Mental States".
Kim, J. 1992 "Multiple Realizability and the Metaphysics of Reduction"
Philosophy and Phenomenological Research 52, 1-26. Reprinted in
Kim's Supervenience and Mind, Cambridge: Cambridge University Press,
1993, 309-336
Kim, J. 1993a "Postscripts on Mental Causation," in Kim 1993b,
p. 358-367
Kim, J. 1993b Supervenience and Mind, Cambridge: Cambridge University
Press, 1993
Kitcher, P. 1980 "How to Reduce a Functional Psychology" Philosophy
of Science 47, 134-140
Kitcher, P. 1982 "Genes, Reduction and Functional Psychology,"
Philosophy of Science 33, 337-359
Nagel, E. 1961, The Structure of Science, London: Routledge and
Kegan Paul
Nathan, P. 1985 "Pain and Nociception in the Clinical Context"
Philosophical Transactions of the Royal Society, London B 308, 219-226
Oppenheim, P. and Putnam, H. 1958"Unity of Science as a Working
Hypothesis". In H. Feigl, M. Scriven & G. Maxwell eds, Minnesota
Studies in the Philosophy of Science Vol II, Minneapolis: University
of Minnesota Press.
Papineau, D. 1985: "Social Facts and Psychological Facts",
in Currie, G. And Musgrave, A. (Eds.) Popper and the Human Sciences.Nijhoff:
Dordrecht, 57-71.
Papineau, D, 1993 "Reduction and Selection", Chapter 2 of
Philosophical Naturalism Blackwell: Oxford, p 33-51
Pereboom, D. And Kornblith, H, "The Metaphysics of Irreducibility",
Philosophical Studies 63, 125-145
Putnam, H., 1965 "Brains and Behavior" in Analytical Philosophy
Vol 2, R. J. Butler, ed. Oxford:Blackwell. Reprinted in Block, 1980a
Putnam, H. 1967 "The Nature of Mental States, in W. Capitan and
D. D. Merrill, eds., Art, Mind and Religion Pittsburgh, 37-48. Reprinted
in Block, 1980a
Putnam, H., 1975, "Philosophy and Our Mental Life", Chapter
14 of Putnam's Mind, Language and Reality: Philosophical Papers,
Vol. 2. Cambridge: Cambridge University Press. Reprinted in Block, 1980a.
Richardson, R. 1979 "Functionalism and Reductionism" Philosophy
of Science 46, 533-558
Shepard, R. 1987 "Toward a Universal Law of Generalization for
Psychological Science" Science 237, 1317-1323
Shepard, R. 1994 "Perceptual-cognitive Universals as Reflections
of the World", Psychonomic Bulletin and Review 1 (1), 2-28
Notes
1. The argument appears mainly in Kim 1992, but it
is foreshadowed in Kim 1972, and various features of it are distributed
in other parts of Kim 1993b, especially in Kim 1993a and in some unpublished
papers. Other critiques of the multiple realizability argument have appeared
in Richardson (1979), Enç (1983), Churchland (1986) and Bealer (1994).
Pereboom and Kornblith (1991) argues against Kim, Kitcher (1980, 1982)
argues against Richardson, and Blackburn (1993) argues against Enç
and Churchland.
2. These examples have flaws. Rigidity
is not the best example of an 'upper level' property in the sense discussed
here. Rigidity is actually a property of basic level mechanics. Mechanics
is not basic in the sense of the Oppenheim/Putnam hierarchy; it is no more
appropriate to elementary particles than to solar systems. It stands apart
from that hierarchy.
And there is another flaw common to both the computation and the peg/hole
analogy: both are more matters of mathematics than empirical science. Geometry
carries the weight in the peg/hole case. And in the program case, once
the program and the error are fully specified, explaining the error in
terms of a glitch in the program is like explaining sleep in terms of dormitivity.
If the error is printing a '1' where there should be a '0', and the program
dictates that a '1' should be printed in that circumstance, then explaining
the output in terms of the program is trivial. The reason I use them is
that they have the virtues of their vices. Being trivial, they do not require
any empirical knowledge and are easy to understand. The thermodynamics/statistical
mechanics example presented in Nagel (1961) is far better for the points
I am making here but takes a lot of space to spell out.
3. Kim tends to use pain as an example.
In my view, thought is a much better candidate for multiple realization
and for being a functional property.
4. The 'tacking paradox' derives an
absurdity from 2 principles: (1) If P entails Q, then evidence that confirms
P also confirms Q, and (2) If T entails a that a certain datum will be
observed, then that datum confirms T. The absurdity is much like the one
in the text. If theory T entails datum-sentence D, then by (2) D confirms
T. Conjoin T with anything at all, arbitrary claim A. T&A also entails
D and so is cofirmed by D. But T&A entails A, and so by (1), D confirms
A. But A was arbitrary. In effect, we have derived that anything confirms
anything. The role of the 'well' is to keep D from confirming T&A.
A generalization is confirmed by a datum only if it confirms 'all' of it.
Thus 'arthritis or lupus' is projectible (relative to the hypothesis) only
if the evidence that well confirms 'Anyone who has arthritis is helped
by Ibuprofen' also well confirms 'Anyone who has arthritis or lupus is
helped by Ibuprofen'. Thus the projectibility of the disjunctive predicate
depends on whether the evidence that confirms 'Anyone who has arthritis
or lupus is helped by Ibuprofen' confirms 'all' of it. The upshot is that
what makes the disjunctive predicate 'arthritis or lupus' unprojectible
(relative to melioration by Ibuprofen) is that evidence of melioration
by Ibuprofen can be relevant to confirmation of 'part' of the disjunction
but not 'all' of it. The upshot is that there is not an enormous distance
between the Principle used by Kim and the conclusion that heterogeneous
disjunctions are not projectible. But that is no problem if the Principle
is true.
5. Actually, the realizations can
be second order and according to me, dormitivity itself can be one of them.
See Block (1990) for a discussion of some of these peculiarities. I will
ignore these complications here.
6. One form of computational structure,
production systems, could be realized in liquid form. An input-output conditional
floats in a soup, waiting for the right output from another conditional
to trigger its output. But the larger and more complex the computational
structure of thought, the less plausible this sort of system seems as a
realization of thought.
7. This paper was presented at the
Pacific APA meeting in March, 1995 in San Francisco at a symposium on the
work of Jaegwon Kim. It was also presented at the Centre de Recherche en
Epistémologie Appliquée in Paris, at the meeting of the Società
Italiana di Logica e Filosofia delle Scienze in Rome in January, 1996,
at University College London, at the University of Maribor, Slovenia and
at the CUNY Graduate Center.. I am grateful for comments to Alex Byrne,
Noam Chomsky, Jerry Fodor, Ned Hall, Paul Horwich, Jaegwon Kim, Noa Latham,
David Papineau and Daniel Stoljar. I discovered after writing this paper
that elements of the points made by Kim and my reply were anticipated in
a series of papers by David Papineau, notably Papineau 1985 and 1993

