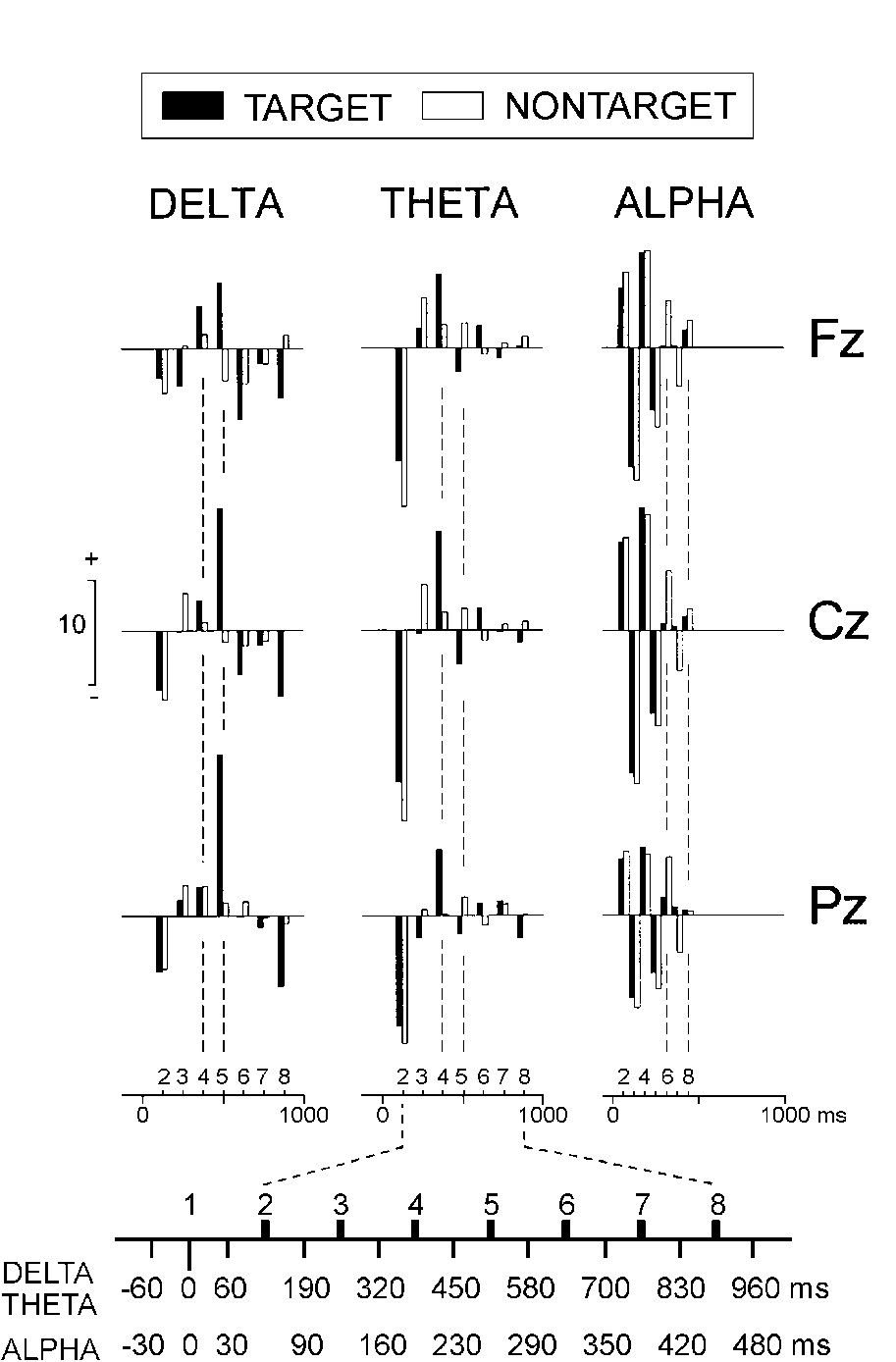Kolev, V., Demiralp, T., Yordanova, J., Ademoglu,
A., Isoglu-Alkaç, Ü. (1997). Time-Frequency Analysis Reveals
Multiple Functional Components During Oddball P300. NeuroReport,
8: 2061-2065.
Copyright © 1997 Rapid Science Publishers
Time-Frequency Analysis Reveals Multiple Functional Components During Oddball
P300
Vasil Kolev 2,
Tamer Demiralp 1,3,CA,
Juliana Yordanova 2,
Ahmet Ademoglu 4,
and Ümmühan Isoglu-Alkaç 1,3
1 Istanbul University, Electro-Neuro-Physiology
Research and Application Center, 34390 Çapa-Istanbul, Turkey,
2 Institute of Physiology, Bulgarian
Academy of Sciences, Acad. G. Bonchev str. bl. 23, 1113 Sofia, Bulgaria,
3 Turkish Scientific and Technical
Research Council (TÜBITAK), Brain Dynamics Research Unit, 06100
Kavaklidere-Ankara, Turkey,
4 Bogaziçi University,
Institute of Biomedical Engineering, Bebek-Istanbul, Turkey
CA Corresponding Author:
Assoc. Prof. Dr. Tamer Demiralp
Istanbul University
Istanbul Faculty of Medicine
Department of Physiology
34390 Çapa-Istanbul, Turkey
Tel (Fax): 90 212 533 94 68
e-mail: karamusa@hamlin.cc.boun.edu.tr
Abstract
A time-frequency decomposition was applied to rare target and frequent
non-target event-related potentials (ERPs) elicited in an oddball condition
to assess whether multiple functional components occur in the P300 latency
range. The wavelet transform (WT) was used because it allows capture of
simultaneous or partly overlapping components in ERPs without loosing their
temporal relationships. The application of a four-octave quadratic B-spline
wavelet transform at the level of single-sweep data allowed us to obtain
new information and revealed the presence of separate events during P300
development. Several delta, theta, and alpha frequency components in the
P300 latency range differed between target and non-target processing. These
findings indicate that P300 is composed of multiple functional components
and that the WT method is of use for the study of P300 functional correlates
more precisely.
Key words: Cognitive processes, Event-related
brain potentials (ERPs), P300 (P3) wave, Time-frequency analysis, Wavelet
transform (WT)
Introduction
Event-related brain potentials (ERPs) are time-varying signals which
reflect the summated time-courses of underlying neural events during information
processing. The processing mechanisms may operate on different time scales,
from milliseconds to seconds, and may also be entirely or partly overlapping.
To separate functionally meaningful events that occur simultaneously, different
procedures or statistical methods have been applied to the ERP waveforms
(e.g., Refs. 1-3), but the reliable component isolation remains problematic.
Recently, an efficient time-frequency (time-scale)
decomposition method, the wavelet transform (WT), was proposed as a tool
to examine the multicomponent structure of ERPs [4-6]. The major advantage
of the WT is its variable time resolution involving shorter effective time
windows for higher frequencies reflecting fast and short-duration
processes and longer effective time windows for lower frequencies reflecting
slow processes. The WT can therefore partition the ERP between several
orthogonal functions (independent frequency components) with parallel time
courses, thus respecting the overlapping component composition of ERPs
[4,5,7]. These wavelet functions can be chosen such that they are well
localized in time, which allows description of the time positions of events
in different frequency ranges.
According to many previous reports, a late positive
wave P300 with a parieto-central distribution is consistently elicited
by rare attended stimuli presented in an oddball task [8-10]. Similar late
positive waves have been recorded in various other conditions where low
probability, novel, or task-relevant (to-be-attended, to-be-memorized,
or to-be-responded) stimuli are used [9,11]. P300 waves have shown condition-specific
shapes, latencies, and scalp topographies [12]. In addition, different
sites of P300 origin have been proposed. These observations imply
that even when P300 appears as a single wave, it is not a unitary phenomenon
but may have a heterogeneous and multicomponent structure. For example,
in the classical oddball condition, P300 is typically seen as a single
wave or as a bifid wave in some cases [10]. However, stimulus probability,
novelty, discriminability, task-relevance, etc. are all processed in the
oddball condition. Each of these variables alone is known to affect P300
and may relate to several distinct subcomponents, but P300s with simple
shapes are usually observed in the time domain ERP. In the frequency domain,
delta (0.5-4 Hz) and theta (4-7 Hz) responses in the P300 latency range
have been shown to differ between rare target and frequent non-target processing
[13-15]. Given the advantages of the multiresolution time-frequency analysis
provided by the wavelet transform, the present study was undertaken to
examine whether multiple functional components can be disclosed within
the oddball P300 and whether such components might correspond to those
previously described.
Materials and Methods
Ten healthy volunteers (age 18-27 years; six females) served as subjects.
Electroencephalogram (EEG) was recorded at Fz, Cz, and Pz locations (10/20
system) with reference to linked mastoids. The cut-off frequencies of the
EEG amplifiers were 0.5 and 70 Hz (-3 dB/oct.), and 1 s pre- and 1 s post-stimulus
epochs were sampled with a frequency of 256 Hz (12 bit). The electro-oculogram
was also recorded. Eighty tones with intensity of 60 dB SPL, duration of
1000 ms, and r/f 10 ms were presented binaurally in an oddball condition.
Two types of auditory stimuli (frequent 2000 Hz and rare 1950 Hz) were
mixed randomly with a probability of 0.2 for the rare tones. The
rare tones were the targets and had to be counted silently. Interstimulus
intervals varied randomly between 3.5 and 5.5 s. During the experimental
session the subjects kept their eyes closed. After the experiment they
reported the number of the counted target stimuli which was in all cases
correct.
After artifact rejection, only sweeps not exceeding
± 45 µV and free of ocular and muscular artifacts were accepted
for further processing. In the averaged ERPs, P300 peak latency and base-to-peak
amplitude values were measured and statistically analyzed.
The wavelet transform was applied to both averaged
and single-sweep ERPs (see bellow). A quadratic B-spline wavelet was used
as having a basic waveshape especially applicable to single EEG data and
providing for near optimal time-frequency localization [5,6,16,17]. A fast
WT algorithm was employed in a standard pyramidal filter scheme to decompose
average and single trial ERPs into the time-frequency plane [4,18]. The
application of a four-octave wavelet transform yielded four sets of coefficients
in 32-64 Hz (gamma), 16-32 Hz (beta), 8-16 Hz (alpha) and 4-8 Hz (theta)
frequency ranges and residues in the 0.5-4 Hz (delta) frequency range.
Each octave contained the number of coefficients appropriate to display
the time resolution relevant for the respective frequency range (Fig.
1A). The interpolation of the coefficients by the quadratic spline
functions can be used to reconstruct the analyzed signal and to represent
the time course in each frequency band (Fig. 1B).
In the present study, delta, theta, and alpha coefficients were evaluated.
Eight delta, eight theta, and 16 alpha coefficients were obtained for each
1 s post-stimulus epoch, with the window size being 128 ms for delta and
theta and 64 ms for the alpha scale. Only the coefficients in the P300
latency range (300-550 ms) were analyzed. These were coefficients 4 and
5 for delta and theta ranges, and coefficients 6, 7, and 8 for alpha range
(Fig. 2). The wavelet coefficients are designated
with a letter corresponding to each frequency band (D for delta, T for
theta, and A for alpha) together with the coefficient number and two other
numbers in brackets representing the approximate time window in ms. For
example, D5(450-580) denotes the fifth delta coefficient obtained for the
450-580 ms epoch.
The wavelet coefficients of single sweep and averaged
ERPs were subjected to repeated measure analysis of variance (ANOVA) with
two within-subjects factors, stimulus (target vs non-target) and
lead (Fz, Cz, and Pz). Amplitude measures of the P300 ERP components were
subjected to the same analysis.
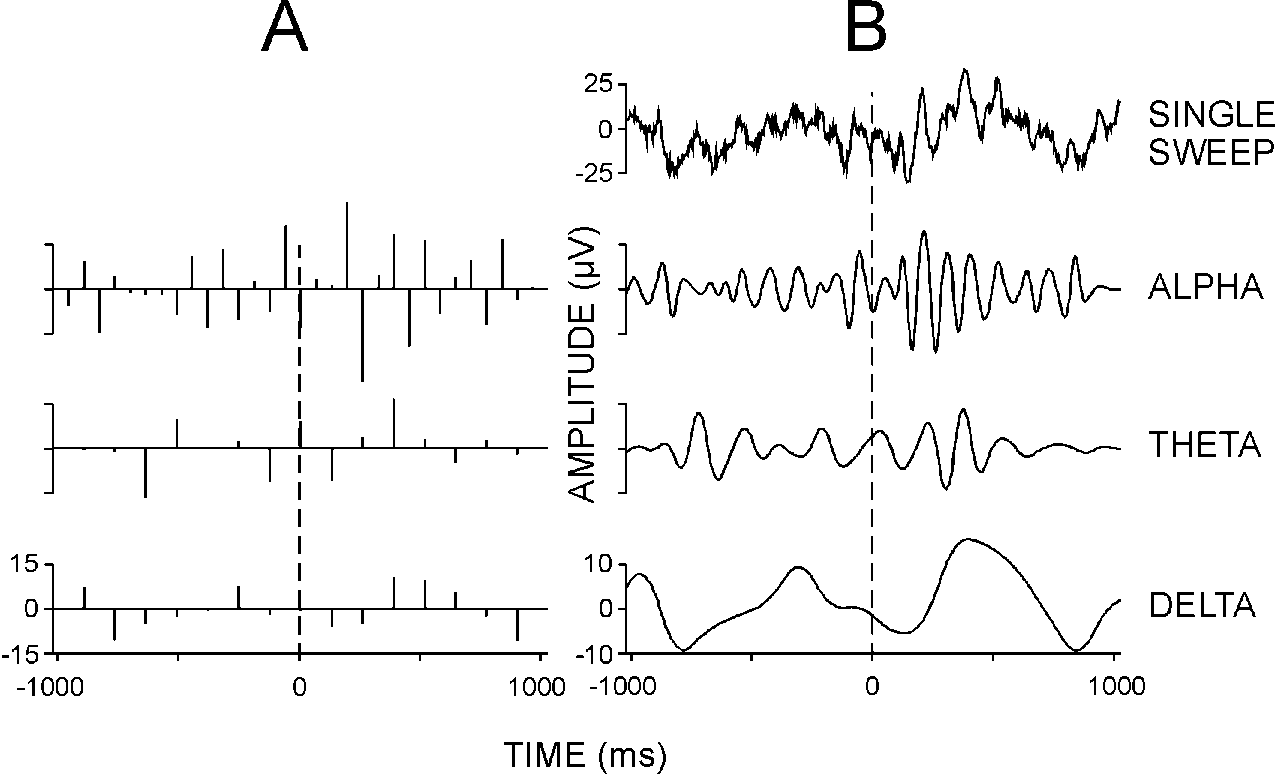
| FIG. 1. One single-sweep recorded from the human
scalp (frequency limits 0.1-70 Hz) after application of auditory target
stimulus. (A) WT coefficient sets in the 8-16 Hz (alpha) and 4-8
Hz (theta) frequency ranges, and the residues in the 0.5-4 Hz (delta) frequency
band. Each octave contains the number of coefficients which is appropriate
to display the relevant time resolution for that frequency range. The interpolation
of the coefficients by spline functions can be used (B) to visualize
the single-sweep time course in each frequency band. |
Wavelet transform: The WT analysis provides an optimal
mathematical solution for time-frequency representation of complex signals,
which is achieved by using a wavelet basis function [4-7,16,17]. The WT
includes the following principal operations: (1) logarithmic scaling
(or frequency decomposition) of the signal, which yields logarithmically
ordered band-pass filters falling into different octaves. Thus, the ratio
between the central frequency of the band-pass and the band-width is preserved
constant, which improves the identification and discrimination of the time-scale
components even if they are overlapped by other non-relevant signals [4].
(2) Linear shifting of the wavelet basis function in each scale (frequency
band) where the scaled basis functions are used to obtain weighting coefficients
resulting from the interaction of the wavelet basis function with the real
signal. This allows for time localization of components in each frequency
band in a manner that guarantees the separability of the captured component
in time and frequency.
Spline basis functions: The B-splines (Fig.
3) of order n are a basis of the subspace of all continuos piecewise
polynomial functions of degree n with derivatives up to n-1
that are continuous everywhere on the real line [16,17]. For equally spaced
integral knot points, any function 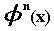 of this space can be expressed as:
of this space can be expressed as:
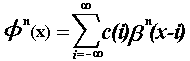
(1)
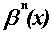 denotes
the normalized B-spline function of order n with n + 2 equally
spaced knots. The definition of
denotes
the normalized B-spline function of order n with n + 2 equally
spaced knots. The definition of 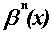 is
is
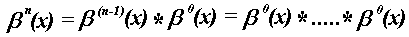 n +
n + 1 times
(2)
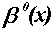 is the indicator function in the interval [0,1] defined as
is the indicator function in the interval [0,1] defined as
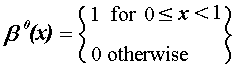
(3)
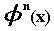 in (1) can be uniquely determined by its B-spline coefficients {c(i)}.
For the B-spline interpolation, the essential point is to determine the
coefficients of this expansion so that
in (1) can be uniquely determined by its B-spline coefficients {c(i)}.
For the B-spline interpolation, the essential point is to determine the
coefficients of this expansion so that 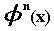 matches the values of some discrete sequence {f(k)} at the knot
points:
matches the values of some discrete sequence {f(k)} at the knot
points: 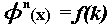 for
for 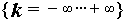 .
The discrete B-splines are obtained by sampling the corresponding continuos
functions
.
The discrete B-splines are obtained by sampling the corresponding continuos
functions 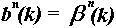 .
Then, the interpolating function
.
Then, the interpolating function 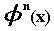 is in the form
is in the form
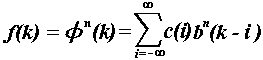
(4)
The B-spline filter coefficients {c(k)} can be
computed for the case of second order (n = 2) using
c+ (k) = f(k) + b1c+
(k-1)
(k = 2,....,K)
(5a)
c- (k) = f(k) + b1c-
(k+1)
(k = K-1,....,1)
(5b)
c (k) = bo(c+(k) + c-(k)
- f(k))
(5c)
where b0 = -8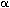 /(1-
/(1-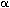 2),
b1 =
2),
b1 = 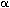 =
=  8 - 3
[16,17].
8 - 3
[16,17].
The fast wavelet transform algorithm: The initial
step for the wavelet decomposition up to a level I is to find the
coefficients {c(k)} at the resolution level 0 (Eqns 6a-b). The wavelet
coefficients {di(k)} are then computed iteratively for
i = 0 to i = I-1 by filtering and decimating by factor
of 2.
c(i+1)(k) = [h*c(i)] (k)
(6a)
(k)
(6a)
d(i+1)(k) = [g*c(i)] (k)
(6b)
(k)
(6b)
i = 0,1,2,.....I-1
where  indicates downsampling by 2 and where h and g are the low-pass
and the high-pass filters for decomposition respectively.
indicates downsampling by 2 and where h and g are the low-pass
and the high-pass filters for decomposition respectively.
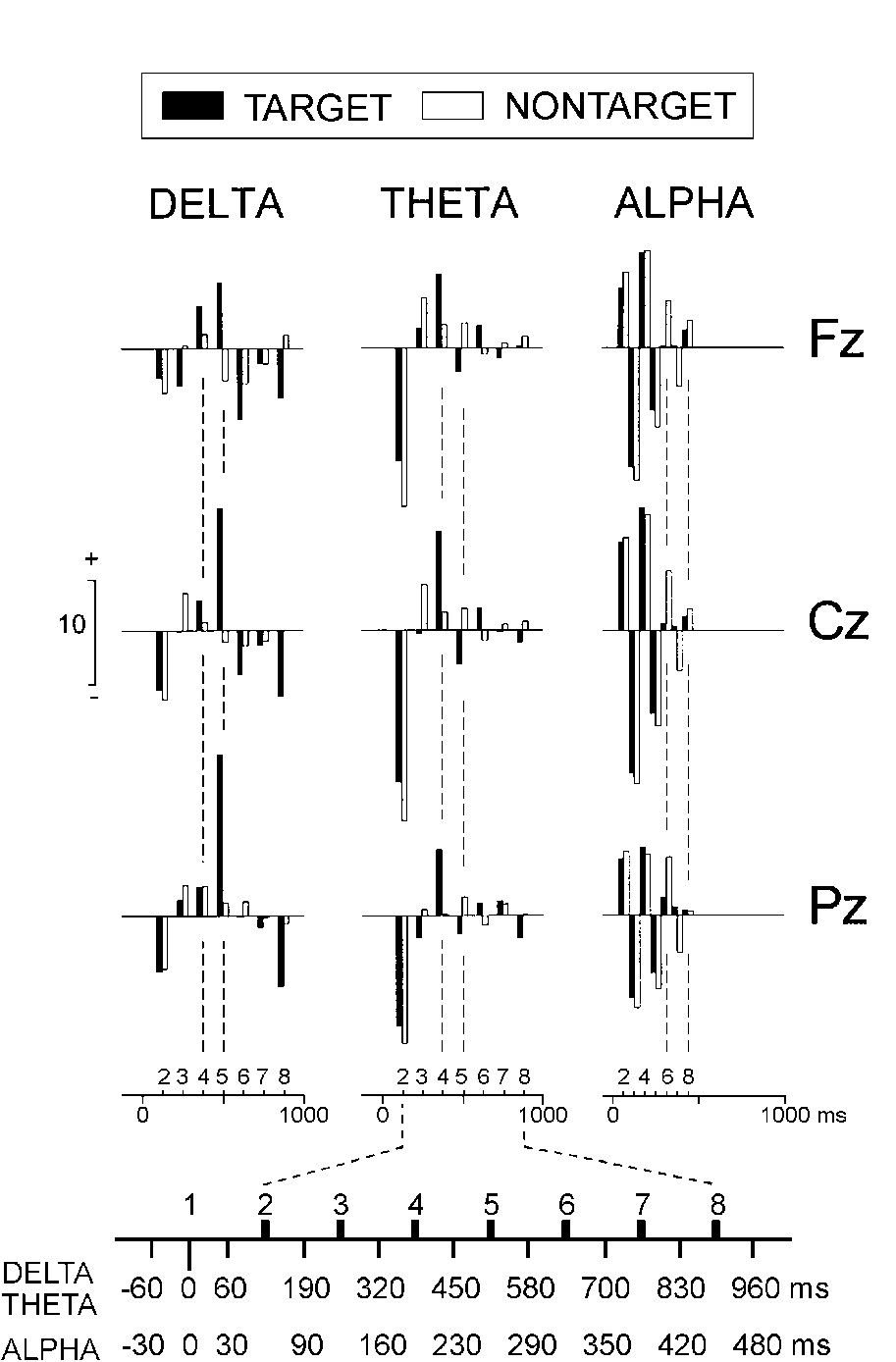
| FIG. 2. Mean values of the analyzed delta, theta,
and alpha wavelet coefficients of oddball target and non-target single
responses at three electrode locations. The time windows of the multiresolution
decomposition and the designation of the coefficients are presented at
the bottom. |
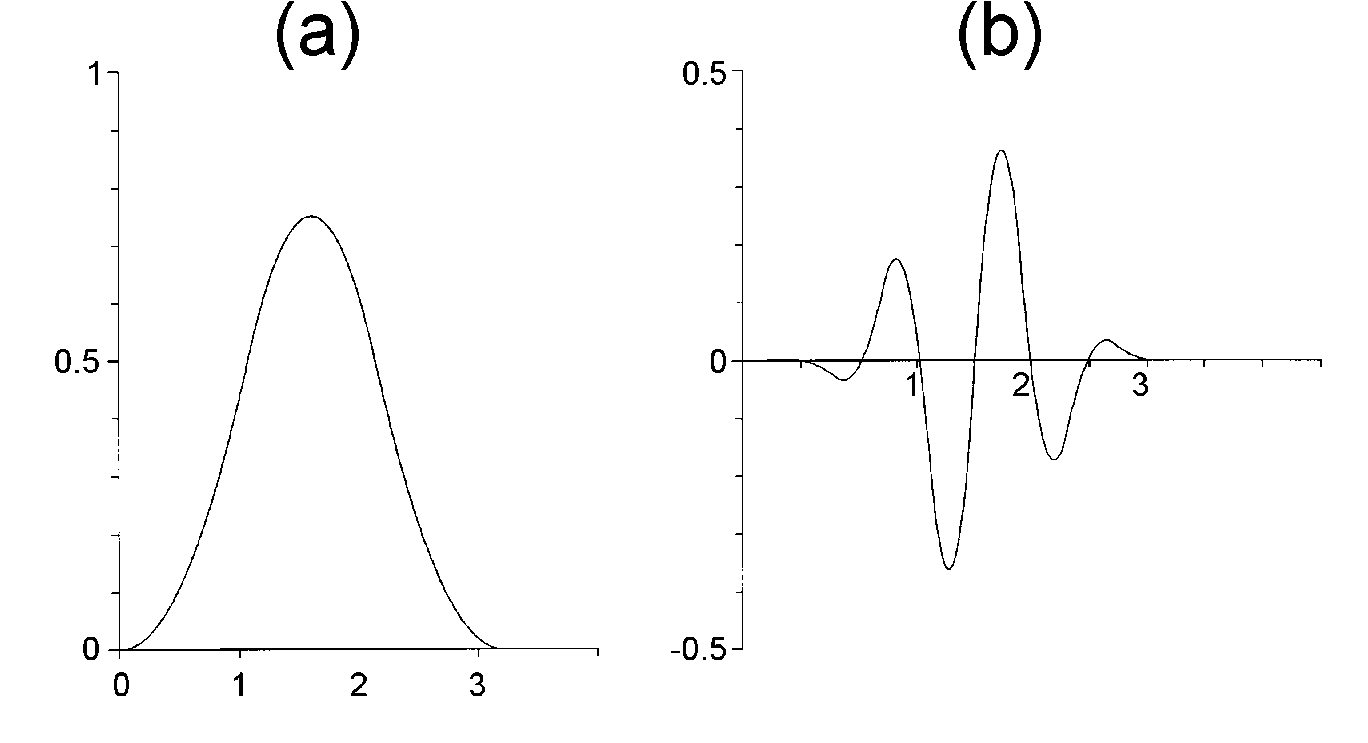
FIG. 3. (a) Quadratic B-spline wavelet function  and (b) the associated spline wavelet
and (b) the associated spline wavelet  . . |
Results
Grand average ERPs from oddball target and non-target stimuli are presented
in Fig. 4 and illustrate that the P300 amplitude was
significantly larger (stimulus, F(1/9) = 29.3; p < 0.001, mean
11.6 vs 3.2 µV) and P300 peak latency was longer (mean 410
ms vs 335 ms) for targets than for non-targets. P300 amplitude was
maximal at Pz (lead, F(2/9) = 35.3; p < 0.001).
Figure 2 shows group mean values
of single-sweep delta, theta, and alpha wavelet coefficients. D4(320-450)
did not depend on the lead and was significantly larger for targets only
at the fronto-central sites (stimulus x lead, F(2/1366) = 11; p
< 0.001; simple stimulus effects at Fz and Cz, F(1/683) > 3.8; p
< 0.05). A most remarkable stimulus type effect was obtained for the
parietally predominant fifth positive delta coefficient D5(450-580) (lead,
F(2/1366) = 198.8; p < 0.001), which was significantly larger
for targets at all electrodes (stimulus, F(1/683) = 156.9; p <
0.001), with this difference being most pronounced at Pz (stimulus x lead,
F(2/1366) = 26.6; p < 0.001). As also illustrated in Fig.
2, targets produced a significantly larger T4(320-450) at the three
locations (stimulus, F(1/683) = 16.7; p < 0.001). This coefficient
was maximal at the centro-frontal locations (lead, F(2/1366) = 11.3; p
< 0.001). The alpha coefficients A6(290-350) and A7(350-420)
were smaller for the targets (stimulus, F(1/683) > 8; p < 0.001)
and did not manifest any dependence on the electrode location. In the averaged
ERPs, similar statistical results were obtained for delta and theta coefficients,
and no significant effects were found for the alpha coefficients.
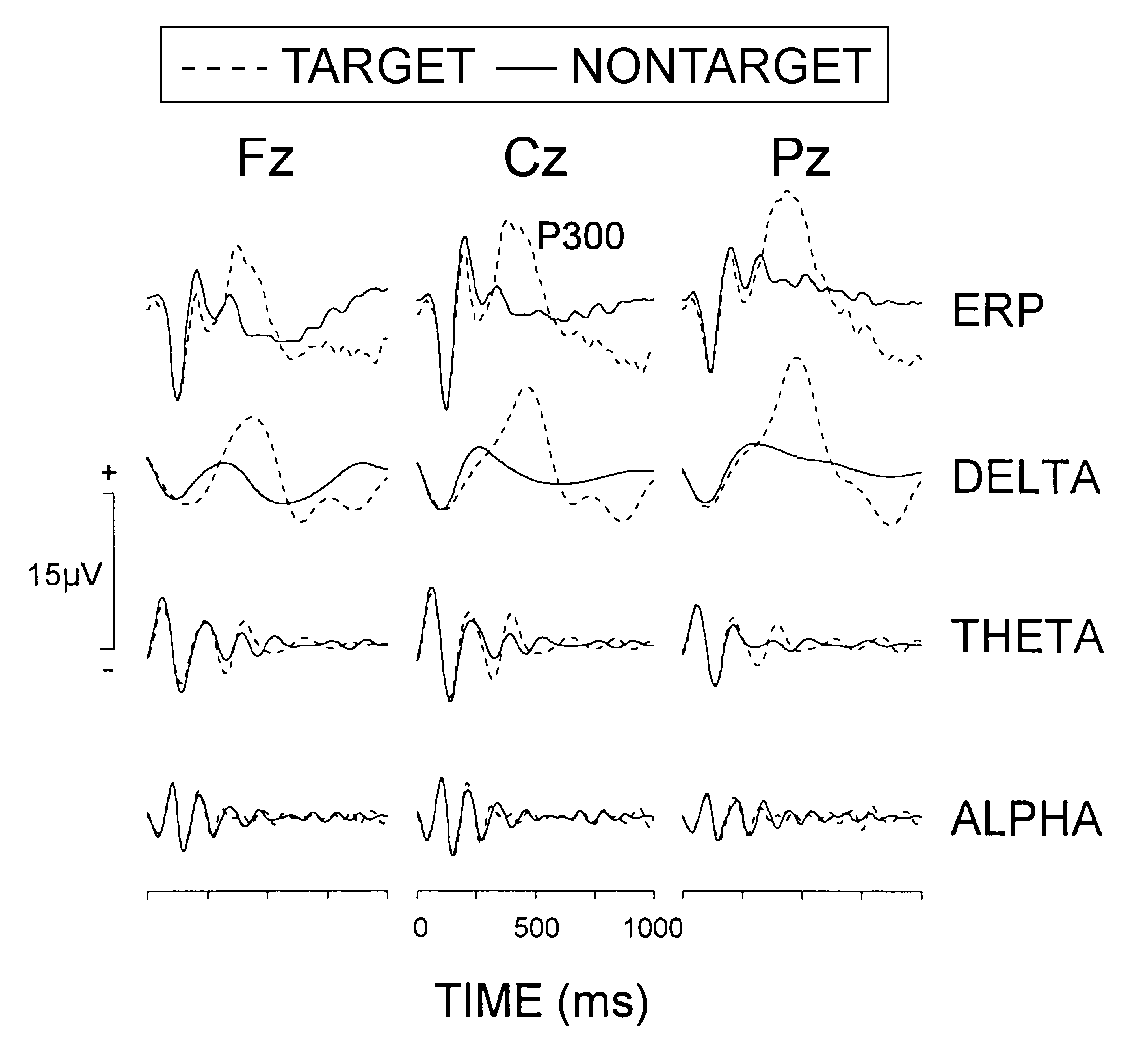
| FIG. 4. Grand average ERPs from oddball non-target
and target stimuli and the reconstructed delta (0.5-4 Hz), theta (4-8 Hz),
and alpha (8-16 Hz) frequency components. Stimulus onset occured at 0 ms. |
Discussion
The present results confirmed previous reports and demonstrated that
the amplitude of the late positive wave P300 was significantly larger to
oddball targets than to frequent non-targets and was maximal at the parietal
location [8-10]. In the averaged potentials, the P300 appeared as a pronounced
single ERP wave. However, the wavelet analysis revealed that during the
oddball task multiple functional components were present in the P300 latency
range. First, the WT partitioned the ERPs among independent time-frequency
components that also manifested specific scalp topography patterns. Therefore,
it is likely that the time-frequency components from the P300 latency range
reflect distinct functional subprocesses that occur during P300 development.
Because these subprocesses are simultaneous or partly overlapping, they
cannot be distinguished in the oddball P300 potential obtained by means
of time domain analysis. Second, the time-frequency components differed
significantly between oddball targets and frequent non-targets, which indicates
that they are functionally meaningful and relevant to oddball task processing.
Hence, separate functional mechanisms appear to be involved in the early
and late stages of P300 expression.
Previous results have shown that a P300 with a relatively
short latency and frontal predominance, called P3a, can be elicited when
the oddball stimuli are extremely rare, surprising, or novel [8,19,20].
It is likely that similar processes are activated during the classical
oddball condition, but P3a could not be distinguished in the averaged ERP.
With regard to the present WT findings it may be assumed that these processes
are reflected by the fronto-central theta components T4(320-450) and by
the simultaneous delta D4(320-450) component that was significantly larger
for the oddball targets at fronto-central sites. It is noteworthy that
these early target vs non-target differences were accompanied by
a wide-spread decrease in alpha (A6 and A7) components to targets, which
is in accordance with previous studies, in which alpha desynchronization
was described for less precisely localized time windows [21].
The rare stimuli in the present study were also
task-relevant. Task-related P300 is recognized typically as a parietal
wave with longer latency (P3b) or as a late positive complex [9,11,22,23].
The WT analysis yielded a later delta coefficient D5(450-580) with a parietal
predominance, which differed most markedly between targets and non-targets.
Given also the findings of the contribution of delta activity to P3b expression
[18,24,25], this delta component is most probably associated with P3b.
Conclusion
By applying the wavelet analysis, the present results reveal the presence
of several functional components in the P300 latency range during an oddball
condition. Further research on the specific responsiveness of the
time-frequency components to cognitive variables known to modulate P300
might lead to a more precise evaluation of the functional correlates of
this endogenous potential.
References
1. Basar E. EEG Brain Dynamics. Relation Between EEG and
Brain Evoked Potentials. Amsterdam: Elsevier, 1980.
2. Näätänen R. Behav Brain Sci 13,
201-288 (1990).
3. Rösler F and Manzey D. Biol-Psychol 13,
3-26 (1981).
4. Samar VJ, Swartz KP and Raghuveer MR. Brain Cog
27, 398-438 (1995).
5. Schiff S, Aldroubi A, Unser M and Sato S. Electroencephalogr
Clin Neurophysiol 91, 442-455 (1994).
6. Ademoglu A, Micheli-Tzanakou E and Istefanopulos Y.
Proc 15th Ann Conf IEEE-EMBS, San Diego, 320-321 (1993).
7. Bartnik EA, Blinowska KJ and Durka PJ. Biol Cybern
67, 175-181 (1992).
8. Pritchard WS. Psychol Bull 89, 506–540
(1981).
9. Picton TW. J Clin Neurophysiol 9, 456-479
(1992).
10. Polich J. P300 in clinical applications: meaning, method,
and measurements. In: Niedermeyer E and Lopes da Silva FH,
eds. Electroencephalography:
Basic Principles, Clinical Applications, and Related Fields. Baltimore:
Williams &
Wilkins, 1993:1005–1018.
11. Polich J and Kok A. Biol Psychol 41, 103–146 (1995).
12. Johnson R Jr. Psychophysiology 30, 90-97 (1993).
13. Basar-Eroglu C, Basar E, Demiralp T and Schürmann M.
Int J Psychophysiol 13, 161-179 (1992).
14. Yordanova
J and Kolev V. Psycoloquy 7-25 memory-brain.7 (1996).
15. Yordanova
J and Kolev V. Psychophysiology 35, 116-126 (1998).
16. Unser M, Aldroubi A and Eden M. IEEE Trans Pattern Anal Mach
Intell 13, 277-285 (1991).
17. Ademoglu A. Analysis of averaged and single evoked potentials using
damped sinusoids and wavelet basis functions.
Ph.D. Thesis. Istanbul: Bogaziçi
University (1995).
18. Demiralp T, Ademoglu A, Schürmann M, Basar-Eroglu C and Basar
E. Brain Cog (in press).
19. Squires N, Squires K and Hillyard S. Electroencephalogr Clin
Neurophysiol 38, 387-401 (1975).
20. Polich J. J Clin Neurophysiol 5, 287-94 (1988).
21. van Dijk J, Caekebeke J, Jennekens-Schinkel A and Zwinderman A.
Electroencephalogr Clin Neurophysiol 83, 44-51
(1991).
22. Squires K, Donchin E, Herning R and McCarthy G. Electroencephalogr
Clin Neurophysiol 42, 1-14 (1977).
23. Picton TW and Stuss DT. Prog Brain Res 54, 17-48
(1980).
24. Pfefferbaum A, Christensen C, Ford J and Kopell BS. Electroencephalogr
Clin Neurophysiol 64, 424-437 (1988).
25. Duncan-Johnson CC and Donchin E. Psychophysiology 16,
53-55 (1979).
Acknowledgements. Supported by the DOPROG Program and
project TBAG Ü 17-3 of the Turkish Scientific and Technical Research
Council (TÜBITAK), Ankara, Turkey, and the National Research Fund
at the Ministry of Science, Education and Technologies, Sofia, Bulgaria.
Received 6 February 1997;
accepted 26 March 1997


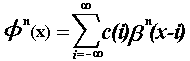 (1)
(1)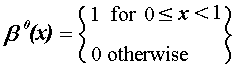 (3)
(3)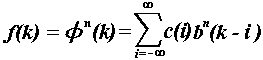 (4)
(4)