To go directly a particular section of this paper, click on a section title below.
| 1. Introduction |
| 2. Conceptual Coherence: Strategies for Making Sense |
| 3. Coherence-driven Conceptual Combination |
| 4. Incoherence-driven Conceptual Combination |
| 5. Conclusion |
Section 2 of this paper uses a newly developed general characterization of coherence to describe how conceptual coherence is assessed whenever thinkers attempt to make sense of a particular situation using the stock of concepts that are available to them as part of their mental systems. Section 3 shows how mundane conceptual combination can be understood in terms of an extended version of such conceptual coherence, as available concepts prove adequate for dealing with a situation. Section 4 describes more creative kinds of conceptual combination that arise because of failures of conceptual coherence.
Kunda and Thagard (in press) have developed a theory of interpersonal impression formation based on the coherence of social concepts. Social stereotypes such as woman, black, and lawyer provide often useful tools for making sense of people we encounter, but their application can be problematic when stereotypes conflict with each other or with particular traits and behaviors that apply to people. What do you make, for example, of a black woman lawyer whose hobby is racing monster trucks? Kunda and Thagard account for a dozen central phenomena of stereotype application by viewing impression formation as a kind of parallel constraint satisfaction, and they present a connectionist model, IMP, that simulates the impression formation of people in many social psychological experiments.
An account of conceptual coherence can naturally be abstracted from IMP. When people are presented with an object or situation, a variety of concepts may potentially apply. The potentially applicable concepts constitute the set of elements that must either be accepted (applied to the situation) or rejected (not applied to the situation). As in IMP, the positive constraints between concepts are the associations between them based on statistical correlations or causal relations. For example, the lawyer concept is for most people associated with concepts such as professional, educated, and intelligent. In contrast, if you have a concept of monster-truck-racer, it is probably associated with working-class and uneducated. Negative constraints between concepts are based either on contradictions (for example between man and woman) or on weaker negative correlations such as that between lawyer and poor. We can now define a conceptual coherence problem as requiring us to apply some concepts to a situation and withhold other concepts in such a way as to maximize the overall satisfaction of the constraints determined by the positive and negative associations between the concepts.
In some situations, such as a black woman lawyer racing monster trucks or colorless green ideas sleeping furiously, conceptual coherence may fail in that the optimal coherence judgment is still not very good. The concepts available to apply to a situation do not fit together well enough to make minimal sense of that situation. Satisfying some constraints requires violating too many other constraints for the conceptual interpretation to be admissible, even though it is the best available. Such failures of intelligibility may call into question a thinker's whole system of concepts and even lead to conceptual revolutions (Thagard, 1992).
Conceptual coherence is an instance of coherence conceived of as maximization of constraint satisfaction. Here is a sketch of a general theory of coherence that is developed in more detail elsewhere (Thagard and Verbeurgt, forthcoming).
1. Elements are representations such as concepts, propositions, parts of images, goals, actions, and so on.Many kinds of cognition, including. hypothesis evaluation, concept application, analogy, and decision making, are coherence problems.2. Elements can cohere (fit together) or incohere (resist fitting together). Coherence relations include explanation, deduction, facilitation, association, and so on. Incoherence relations include inconsistency, incompatibility, and negative association.
3. If two elements cohere, there is a positive constraint between them. If two elements incohere, there is a negative constraint between them.
4. Elements are to be divided into ones that are accepted and ones that are rejected.
5. A positive constraint between two elements can be satisfied either by accepting both of the elements or by rejecting both of the elements.
6. A negative constraint between two elements can be satisfied only by accepting one element and rejecting the other.
7. The coherence problem consists of dividing a set of elements into accepted and rejected sets in a way that satisfies the most constraints.
More formally, Thagard and Verbeurgt (forthcoming) define a coherence problem as follows. (2) Let E be a finite set of elements {ei} and C be a set of constraints on E understood as a set {(ei, ej)} of pairs of elements of E. C divides into C+, the positive constraints on E, and C-, the negative constraints on E. With each constraint is associated a number w, which is the weight (strength) of the constraint. The problem is to partition E into two sets, A and R, in a way that maximizes compliance with the following two coherence conditions:
1. if (ei, ej) is in C+, then ei is in A if and only if ej is in A.Let W be the weight of the partition, that is, the sum of the weights of the satisfied constraints. The coherence problem is then to partition E into A and R in a way that maximizes W. Because a coheres with b is a symmetric relation, the order of the elements in the constraints does not matter.2. if (ei, ej) is in C-, then ei is in A if and only if ej is in R.
Maximizing coherence is a difficult computational problem: Verbeurgt has proved that it belongs to a class of problems generally considered to be computationally intractable, so that no algorithms are available that are both efficient and guaranteed correct. Nevertheless, good approximation algorithms are available. Here is how to translate a coherence problem into a problem that can be solved in a connectionist network:
1. For every element ei of E, construct a unit ui which is a node in a network of units U. These units are very roughly analogous to neurons in the brain.We then get a partition of elements of E into accepted and rejected by virtue of the network U settling in such a way that some units are activated and others rejected. Intuitively, this solution is a natural one for coherence problems. Just as we want two coherent elements to be accepted or rejected together, so two units connected by an excitatory link will be activated or deactivated together. Just as we want two incoherent elements to be such that one is accepted and the other is rejected, so two units connected by an inhibitory link will tend to suppress each other's activation with one activated and the other deactivated. A solution that enforces the two conditions on maximizing coherence is provided by the parallel update algorithm that adjusts the activation of all units at once based on their links and previous activation values.2. For every positive constraint in C+ on elements ei and ej, construct an excitatory link between the corresponding units ui and uj.
3. For every negative constraint in C- on elements ei and ej, construct an inhibitory link between the corresponding units ui and uj.
4. Assign each unit ui an equal initial activation (say .01), then update the activation of all the units in parallel. The updated activation of a unit is calculated on the basis of its current activation, the weights on links to other units, and the activation the units to which it is linked. A number of equations are available for specifying how this updating is done. Typically, activation is constrained to remain between a minimum (e.g. -1) and a maximum (e.g. 1).
5. Continue the updating of activation until all units have settled - achieved unchanging activation values. If a unit ui has final activation above a specified threshold (e.g. 0), then the element ei represented by ui is deemed to be accepted. Otherwise, ei is rejected.
The characterization of coherence in terms of constraint satisfaction applies equally well to work on explanatory coherence (Thagard, 1992), analogical coherence (Holyoak and Thagard, 1995), and deliberative coherence (Thagard and Millgram, 1995). As we saw in the IMP account of stereotype application, conceptual coherence operates with a set of elements that are concepts and a set of constraints based on positive and negative associations between concepts.
In contrast to Shoben and Gagné's abstract relations view, Wisniewski defends a schema approach in which conceptual combination consist essentially in filling a slot in the head noun with a filler suggested by the modifier. Slots represent a large number of possible features or relations, not the small number considered by the abstract relations view. Wisniewski identifies three basic kinds of combinations in English: relation-linking combinations that involve a relation between the referents of the modifier and head concepts; property integration combinations apply one or more properties of the modifier concept to the head concept; and hybrid combinations that either refer to a combination of the constituents or to a conjunction of the constituents.
I will now sketch a coherence-based computational model of how people select the appropriate relations and make other inferences as part of conceptual combination. This model is intended to apply both to the selection of relations found in Shoben and Gagné's account and to the combination of schemas found in Wisniewski's account.
I conjecture that when people encounter a modifier-head combination they unconsciously proceed as follows:
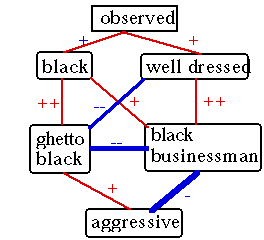
1. Construct a constraint network whose elements are possible inferences to be made concerning the object denoted by the head and whose constraints are based on frequencies of association between the elements associated with the head and modifier.As in the IMP model of Kunda and Thagard (in press), I assume that every concept has a network of associated concepts. The associated concepts include the kind of information required by both the abstract relations and schemas views of conceptual combination. How coherence-based conceptual combination can work is best seen by taking an example of predicating combination where the object denoted by the head has the property denoted by the modifier, as in big dog. In this case, the modifier fills a slot or adds a new slot. Here is a richer example taken from IMP's simulation of the phenomenon of subtyping, in which the inferences normally drawn from a stereotype are overruled by particular information about a person. Some people's stereotypes of blacks come with the association of their being aggressive, perhaps because their stereotypical example of a black is a poor ghetto inhabitant. On the other hand, the combination well-dressed black suggests a different associations, namely with black businessman not expected to be aggressive. Figure 1 shows a constraint network that captures these different associations. To perform the conceptual combination well-dressed black, a person needs to come up with the most coherent interpretation, i.e. the interpretation that best satisfies the constraints. Positive constraints include the associations that ghetto blacks are aggressive, while negative constraints include the negative association that ghetto blacks tend not to be businessmen. IMP uses a connectionist algorithm to judge that the most coherent interpretation of well-dressed black given the associations in Figure 1 involves the rejection of aggressiveness. IMP calculates how to perform the property overlap of the given concepts, but it is also capable of going beyond that overlap to introduce concepts that are associated with associates of the initial concepts. In figure 1, aggressive and its negation are not directly associated with well-dressed or black, but can nevertheless emerge as part of the interpretation of the combined concepts.2. Use connectionist algorithms to do a parallel calculation that maximizes coherence by accepting some elements and rejecting others.
3. The result is an interpretation of the relation between the head and modifier, as well as a collection of inferences about the object denoted by the head as characterized by the modifier.
4. If the most coherent interpretation is nevertheless not very coherent, then move to other mechanisms such as analogy and explanation that produce the incoherence-driven conceptual combinations discussed in the next section.

Figure 1. A constraint network for combining well-dressed and black. Thin lines with pluses indicate positive constraints. Thick lines with minuses indicate negative constraints. This network rejects aggressive, but if well -dressed is not connected to observed, the network accepts aggressive.Although IMP appears adequate to model many predicating conceptual combinations, it is not powerful enough to handle non-predicating combinations such as apartment dog. I conjecture that such combinations will require a broader kind of constraint network in which thematic relations are used to choose the most coherent interpretation, based on semantic knowledge, factual knowledge, and context. How to construct such networks in detail is not obvious, but figure 2 suggests their general structure. The oval nodes in figure 2 represent hypotheses about what kind of relation holds between the head and modifier, including property overlap (as modeled by IMP), property application, location, and so on. Factual knowledge, semantic knowledge, and context all provide positive constraints that support different interpretations to different degrees. Since the different possible relations between the head and modifier are incompatible with each other, there are strong negative constraints between the elements representing different interpretations. Thus non-predicating conceptual combination can also be viewed as a coherence problem that subsumes predicating conceptual combination as a special case. If an IMP-like process achieves sufficient coherence in property overlap, this should support the property overlap node that implies for a particular case that conceptual combination is predicating. For example, the coherence of interpreting the combination small apartment as referring to something which is both an apartment and small would support the property overlap node. Developing a full, detailed, psychologically plausible model of non-predicating as well as predicating conceptual combination will be difficult because of the possible relevance of such a wide range of factual, semantic, and contextual knowledge.
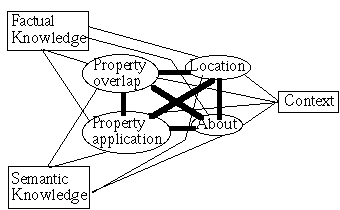
Figure 2. Constraint network for some thematic relations. The thin lines indicate positive constraints, while the thick lines indicate negative constraints.
This example illustrates how failure to find a coherent conceptual combination can lead to a more far-flung search for interpretations that evoke high-level cognitive processes such as analogy. Analogy can also be thought of as a kind of coherence process in which a constraint-satisfying correspondence is found between a source analog and a target analog (Holyoak and Thagard, 1995). But analogy is not the only possible source for new interpretations. Kunda, Miller, and Claire (1990) showed that surprising combinations such as Harvard-educated carpenter and blind lawyer generate causal reasoning in which people form new hypotheses to explain, for example, how someone who is blind could become a lawyer. Hampton (this volume) shows additional examples of how conceptual combination can lead to emergent properties, i.e. properties not originally associated with either the head or the modifier concepts. This kind of emergent conceptual combination is often abductive, in that it involves the formation of explanatory hypotheses to explain how the modifier can apply to the head. (Abductive inference, or abduction as C. S. Peirce dubbed it, involves the formation and acceptance of explanatory hypotheses.) Like scientists, experimental subjects who generate emergent properties using causal/explanatory reasoning realize they need to go beyond recognition of an initial lack of coherence in combined concepts to develop novel coherent interpretations.
Analogy and abduction are the two major sources of theoretical creativity in science (Thagard, 1988, 1992). For example, Darwin's seminal combination, natural selection, was both analogical and abductive: it depended on an analogy to the familiar process of artificial selection by breeders; and it involved the postulation that selection could become natural by virtue of a struggle for existence in the face of reproductive principles. Similarly, the ancient combination sound wave was analogical in that it depended on an analogy between sound and water, and it was abductive in that it used the wave hypothesis to explain the behavior of many sound phenomena such as echoing. Analogy and abduction are not, however, peculiar to creative scientists. In everyday life, people frequently use analogies to solve mundane problems like adapting last year's income tax preparation to do this year's tax forms, and people abductively infer explanations for why their cars fail to start or why their spouses are in a bad mood.
Thus relatively creative conceptual combinations such as web potato and natural selection require leaps beyond the coherence-driven constraint-satisfying reconciliation of associations and thematic relations. They are incoherence-driven in that failure to find a sufficiently coherent interpretation triggers a broader search for an interpretation using analogical and explanatory mechanisms. I am not claiming that all creative conceptual combinations are incoherence-driven, since coherence-driven conceptual combination can produce emergent attributes such as non-aggressive from well-dressed black in figure 1. I conjecture, however, that the most creative conceptual combinations arise from the more constructive and less associative mechanisms of abduction and analogy.
The distinction between coherence-driven and incoherence-driven combinations is analogous to the distinction between additive and multiplicative principles (Wilkening, Schwarzer, and Rümmele, this volume). Just as incoherence-driven conceptual combinations go beyond coherence-driven ones in the complexity of the new inferences they can yield, so multiplicative rules in physics and other domains make possible a richer account of phenomena than additive rules can provide.
1. By "conceptual coherence" I mean the problem of coming up with a coherent interpretation based on multiple concepts. This is different from the problem of conceptual coherence discussed by Murphy and Medin (1985), which concerns why a given set of objects is grouped together to form a category. Another issue not discussed in this paper is the coherence of a whole conceptual system (Thagard, 1993).
2. I borrow a few paragraphs from Thagard and Verbeurgt (forthcoming). The notion of coherence maximizing is an abstraction from connectionist ideas about maximizing goodness of fit or harmony.
Holyoak, K. J., & Thagard, P. (1995). Mental leaps: Analogy in creative thought. Cambridge, MA: MIT Press/Bradford Books.
Kunda, Z., Miller, D., & Claire, T. (1990). Combining social concepts: The role of causal reasoning. Cognitive Science, 14, 551-577.
Kunda, Z., & Thagard, P. (in press). Forming impressions using stereotypes, traits, and behaviors: A parallel constraint satisfaction theory. Psychological Review.
Murphy, G., & Medin, D. (1985). The role of theories in conceptual coherence. Psychological Review, 92, 289-316.
Shoben, E. J., & Gagné, C. L. (this volume). Thematic relations and the creation of combined concepts. In T. B. Ward, S. M. Smith, & J. Viad (Eds.), Conceptual structures and processes: Emergence, discovery, and change Washington, D. C.: American Psychological Association.
Thagard, P. (1988). Computational philosophy of science. Cambridge, MA: MIT Press/Bradford Books.
Thagard, P. (1992). Conceptual revolutions. Princeton: Princeton University Press.
Thagard, P. (1993). Computational tractability and conceptual coherence: Why do computer scientists believe that P not= NP? Canadian Journal of Philosophy, 23, 349-364.
Thagard, P., & Millgram, E. (1995). Inference to the best plan: A coherence theory of decision. In A. Ram & D. B. Leake (Eds.), Goal-driven learning: (pp. 439-454). Cambridge, MA: MIT Press.
Thagard, P., & Verbeurgt, K. (forthcoming). Coherence. Unpublished manuscript, University of Waterloo.
Wilkening, F., Schwarzer, G., and Rümmele, A. (this volume). The developmental emergence of multiplicative combinations. In T. B. Ward, S. M. Smith, & J. Viad (Eds.), Conceptual structures and processes: Emergence, discovery, and change Washington, D. C.: American Psychological Association.
Wisniewski, E. J. (this volume). Conceptual combination: Possibilities and esthetics. In T. B. Ward, S. M. Smith, & J. Viad (Eds.), Conceptual structures and processes: Emergence, discovery, and change Washington, D. C.: American Psychological Association.