|
|
|
|
|
|
|
|
|
a. Initial visible phase |
b. Occlusion phase |
c. Flash and response |
Movement prediction and movement production
Mark Wexler and François Klam
March 1999
Abstract
The prediction of future positions of moving objects occurs in cases of actively produced and passively observed movement. We study the difference between active and passive movement prediction by asking subjects to estimate displacements of an occluded moving target, where the movement is produced by the subject or passively observed; in the passive condition, the target trajectory is either a replay of a preceding active trajectory, or a constant-speed approximation. In the active condition estimates are more anticipatory than in the passive conditions, but in all conditions, estimates become less anticipatory as the prediction distance increases, or the prediction time decreases. Decreasing the congruence between motor action and visual feedback diminishes but does not eliminate the anticipatory effect of action; introducing eye tracking, however, does eliminate it. Our results are compatible with common mechanisms underlying both active and passive movement prediction, with additional movement-related information in the active case making predictions more anticipatory.
Submitted to Journal of Experimental Psychology: Human Perception and Performance
Introduction
How do we predict the future trajectories of moving objects from past experience? Formally, the problem is ill-defined; but in practice, people constantly engage in this type of inductive process: witness one’s surprise at a fast-moving object that goes behind a small occluder and fails to re-emerge forthwith.
From the point of view of a particular observer, object movement may be categorized into two broad types: actively caused and passively observed. Categorizing more finely, actively caused object movement may be direct—movement of a manipulandum that is geometrically similar to the movement of the manipulating limb—or indirect—an object that, due to some mediating mechanism, follows a different path than the manipulator. A passively observed moving object, on the other hand, may or may not be tracked with the eyes. In this paper we study the effect of these forms of object movement on the prediction of future positions of a moving target.
The prediction of movement has been studied separately in the case of motor action (mainly in the case of manual and ocular movement), and in the case of visually observed motion. Before introducing our experiments, we briefly review some of these results. We then present two experiments, whose goal is to compare the dynamics of the prediction process in the actively produced and passively observed movement.
Sensorimotor anticipation
Although efferent-copy theories of motor control have existed for at least a century (Helmholtz, 1866; von Holst & Mittelstaedt, 1950; Sperry, 1950), it is only recently that we have come to appreciate the importance of the prediction of sensory results of motor actions—to be called sensorimotor anticipation—in normal human motor planning and execution. Indeed, any motor system making use of sensory feedback data and where feedback delays are sizeable compared to output delays must supplement actual sensory feedback with predicted feedback, based on an estimate of current state and the motor command simultaneously being planned or executed. Such a predictor, based on current state information and motor commands, is called a forward model.
As Wolpert et al. (1995) point out, sensorimotor anticipation could have the following uses: compensation for delayed sensory feedback; cancellation of sensory effects due to self-produced movement; and the covert trying out of possible actions, to be used, e.g., in motor planning. Over the past decade, direct neurophysiological evidence has been accumulating of neurons or neural ensembles in mammalian brains that predict the sensory consequences of the animal’s action. In the case of locomotion, O’Keefe and Recce (1993) found that the activation packet of place cells in the hippocampus of rats, believed to represent the animal’s current position on a ‘mental map’, undergoes oscillations during which it periodically gets ahead of the current position and transiently represents future position’s on the animal’s path. In the case of manipulation, Eskandar and Assad (1999) have found cells in the posterior parietal cortex of macaques that seem to encode the predicted visual trajectories of occluded targets whose movement is under the animal’s control.
In a task similar to one of the conditions in our experiments, Wolpert et al. (1995) find that subjects overestimate the extent of unseen arm movements, and that this systematic bias has a very specific temporal dynamics: it initially increases, peaks at about one second of movement duration, and then decays. The growth phase is interpreted as being due to the application of a forward model (with a gain that is greater than one, although that is a free parameter), followed by a correction toward zero bias due to proprioceptive feedback. Wolpert et al. postulate a model composed of a predictive mechanism that accepts as input an estimate of current state as well as the efferent copy of current motor commands; this predictor is coupled to a system that stores the current state estimate. Recent neurophysiological evidence points to the cerebellum as a possible site of this predictive mechanism (Blakemore et al., 1998). Neuropsychological evidence suggests that a representation of the current state estimate may be stored in posterior parietal cortex (Wolpert et al., 1998), while the results of Eskandar and Assad (1999) indicate that, at least in macaques, posterior parietal cortex may already encode predictions.
Sensorimotor anticipation has been posited as a mechanism driving cognitive functions as well. Rieser et al. (1986) found that locomotion even in the absence of vision aids in the egocentric re-representation of spatial lay-out. Such visuomotor updating during locomotion could rely on the neural mechanisms documented by O’Keefe and Recce (1993). In a two-task interference study, Wexler et al. (1998) found that a manual rotation made a mental rotation of a visual image faster and more accurate if the two rotations were in the same direction, slower and more error-prone if they were in opposite directions; moreover, when the two rotations were in the same direction, faster motor rotation tended to speed up the mental rotation, while slower motor rotation tended to slow it down. Based on these and other correlations, Wexler et al. (1998) conclude that mental rotation must make use of some mechanisms of the motor system, most likely visuomotor anticipation.
Eye movements and the prediction of motion
Eye movements and their underlying neural mechanisms exhibit a variety of predictive effects. Particularly clear evidence is provided by the study of Duhamel et al. (1992), which documents cells in the monkey parietal cortex that shift their receptive fields in the anticipation of eye saccades. This mechanism could help the animal distinguish visual motion due to gaze shifts from that due to external object movement, and would contribute to stabilizing the visual world in the presence of an unstable retinal image during eye movements.
The dynamics of eye movements in mammals demonstrates their predictive nature. In the smooth pursuit of a visual target that suddenly changes position or speed, for instance, Barnes and Asselman (1992) found that tracking at the target’s old speed continues for a short time after the trajectory change. This phenomenon can be regarded as a prediction by the oculomotor system of the target’s trajectory, based on past data. Saccadic mechanisms also seem to feature predictive properties, as demonstrated by the results of Duhamel et al. (1992) in monkeys.
Anticipatory eye movements may have a special connection to information about the manipulation of objects. For instance, Steinbach and Held (1968) found that the tracking an object that is actively displaced by the observer is more accurate and smooth than tracking a passively observed moving object. Even when no active manipulation of the visual target is involved, eye movements may be especially attuned to biologically produced motion, as compared to more general dynamics. de’Sperati and Viviani (1997) found that tracking a visual target moving around an ellipse is more efficient if the speed profile follows the so-called 2/3 power law, which is actually the profile produced by human subjects making elliptical hand movements when asked to do so at a constant speed.
Eye movements, especially the smooth pursuit system, seems to share mechanisms with conscious speed perception, as demonstrated by numerous details of precision and systematic bias that the two have in common (Post and Leibowitz, 1985; Kowler and McKee, 1987; Beutter and Stone, 1998). The absence of efferent copy of eye movement commands, and consequent lack of prediction of the their sensory effects, seems to lead to false perception of motion in the opposite direction (Haarmeier et al., 1997). Even in the absence of any neurological disorder, anticipatory motion compensation during saccades induces brief misjudgments of position (Cai et al., 1997).
Eye movements are thus probably involved in the perception and prediction of movement. Because of their interaction with manual movement (Steinbach and Held, 1968), the presence or absence of eye movements could have a different effect on actively produced than on passively observed motion.
Passive movement prediction
In a separate and widely dispersed body of work, the prediction of the outcome of passively observed movement has also been studied. The typical protocol that has been used is a target moving in a straight line at a constant speed from point A to point B, and then disappearing behind an occluder. The subject’s task is to press a button when the target is extrapolated to pass behind a marked point, C.
Slater-Hammel (1955) found that subjects typically overestimated tBC, the time to travel between points B and C, by 10 – 20%. In a fixed-speed paradigm, it was found that the overestimation of tBC increased with increasing distance BC, but that the subjective speed in the occluded region (i.e., BC/tBC) increased, approaching its veridical value as BC increased. The visible distance AB, however, had no effect on the predictions, in the range of parameters studied by Slater-Hammel. Ellingstad (1967) varied the target speed and found a similar underestimation of speed for the faster-moving stimuli (7.26 and 1.46°/sec in terms of visual angle), but an overestimation of speed for slower-moving stimuli (0.36°/sec). Bonnet and Kolehmainen (1970) also found that relative speed in the occlusion phase is underestimated in fast-moving stimuli as compared to slow-moving ones; these authors also find an effect of the visible phase, namely that for longer distances AB, the relative speed is underestimated as compared to shorter visible distances. Rosenbaum (1975) studied the prediction of both constant-speed and constant-acceleration trajectories, and presented his results in terms of correlations between objective and subjective speeds and accelerations, and the other kinematics parameters; he found that subjective speeds and accelerations were highly correlated with their objective equivalents, but not with time and distance intervals taken separately. Peterken et al. (1991) varied the time and space variables systematically and independently; they found that the important variable is the time interval tBC over which the prediction is made, with longer prediction intervals leading to predictions that underestimated the target’s displacement. Additionally, Peterken et al. studied the effect of eye movement during the prediction task, introducing a stationary fixation as well as a visual pursuit condition; no significant effect of this manipulation was found.
Prediction of observed movement is not only possible, but in some cases is unconscious, effortless and mandatory, as shown by the so-called ‘representational momentum’ phenomenon (Freyd, 1987). When an observer watches an object undergoing apparent motion, the memory for the final seen position is contaminated by an extrapolation along the object’s apparent trajectory. This involuntary extrapolation shares some characteristics of physical motion: it advances farther for higher initial speeds and for longer time intervals, and appears to slow down and come to rest after a short interval (under 1 sec). This type of involuntary extrapolation is not confined to apparent motion, but can be observed in a variety of illusions in which a moving object appears to be farther advanced than a stationary one (e.g., Müsseler & Aschersleben, 1998).
Experiment 1
The goal of Experiment 1 is to compare the prediction of visual motion in the case when the motion is actively produced to the case where it is passively observed. In the active condition of this experiment, the motor action is congruent to the visual motion: both are rotations, with a visuo-motor gain of 1 (that is, for every degree of motor rotation of the manipulandum, the visual target also rotates by 1 degree).
In order not to confound the motor factor with the response method, we require a technique that does not rely on accurate timed movements, as do the passive movement prediction experiments discussed in the Introduction. We shall therefore use a protocol in which the target briefly reappears following its occlusion, but displaced from its ‘true’ position (resulting from its movement during occlusion) by some deviation. The subject’s two-alternative forced-choice task is to reply whether the target was too far advanced or too far behind relative to where it ought to have been at the moment it re-appeared. The deviation at which the two answers are balanced (as evaluated by fitting the fraction of "too far ahead" answers versus the deviation) is taken as the bias of the subject’s estimate, in any given condition. The reason for this rather indirect method is to avoid a spurious demanding motor task when the variable of interest is precisely the presence of motor action.
In the active condition ("MOT"), subjects displace the visual target by performing a motor action, namely turning a knob, without being able to see their hands. The movement of the target (either a rotation, in Experiment 1, or a translation, in Experiment 2) instantaneously reflects that of the knob. Even though the manipulandum and visual target are spatially separated, there is a compelling illusion of directly acting on the visual target (as in the comparable case of a computer mouse). The subjects were free to decide how fast to perform the motor rotation, but were encouraged to make movements that were as smooth as possible.
In a passive replay condition (to be called "REP"), subjects watch visual displacements produced in one of their own previous MOT trials, but without any manual movement. Matched pairs of MOT-REP trials are identical, save for the presence or absence of the causal motor action. Although the motor movements are quite stereotyped, there are trial-to-trial variations. We worried that these variations could effect predictions; for example, an idiosyncratic MOT trial, in which, say, the subject momentarily hesitates during the occlusion phase, would lead to a REP trial in which the subject, now disconnected from the target, would have no way to predict the feature carried over from the MOT trial. We therefore introduced a second passive control condition ("LIN") in which the trajectory of the target was as predictable as possible—the speed (of rotation or of translation) was constant. This speed was equal to the average speed of a matching active MOT trial.
Method
The subject sat before a computer screen, approximately 50 cm away and at eye level. The subject’s right hand, which was used for turning a knob on some trials, was underneath an opaque cover about 50 cm to the right of the center of the screen, and could not been seen. The subject’s left hand was resting on a computer mouse, which was used for responding.
There were two types of trial: motor (MOT) and visual; in addition, the visual trials were divided into two subtypes, replay (REP) and linear (LIN). A motor trial began with an arrow appearing at the center of the computer screen. The arrow was approximately 5 cm long and 1 cm wide; its geometric center and center of rotation were at the center of screen. The subject turned a knob, which was located to the right of screen. An opaque barrier prevented the subject from seeing either the knob or his wrist. The knob’s face was parallel to the computer screen (so its axis of rotation was perpendicular to the screen), and approximately 5 cm in diameter. The knob had a resolution better than 0.1°, and was sampled at the display frequency, 75 Hz. A Nokia 447X monitor was used to display the visual stimuli, set at the resolution of 0.23 mm/pixel. Only the border of the arrow was drawn––a thick, gray, antialiased line against a black background.
Figure 1 schematically illustrates the protocol. The bottom panel shows the motor action in each of the three phases (in the MOT condition), while the top panel shows the concurrent visual stimulus. In the top panels, only the black arrow corresponds to the actual stimulus; the gray arrow is an attempt to illustrate the subject’s mental representation of the task.
During initial visible phase of the trial (Fig. 1a), the subject turned the knob clockwise. The subject’s rotation was mirrored exactly by the arrow on the screen. The initial orientation of the arrow was randomly chosen and arbitrary, however. The initial visible phase lasted until the knob (and the arrow) turned by an angle of 45°. The subjects were free to choose how fast to turn the knob. This phase lasted 1.2 sec on average. The occlusion phase (Fig. 1b) began with the arrow disappearing; subjects were told to "continue turning the knob at about the same speed as before, and to keep track as best as possible of where the arrow is, even though it is invisible." The occlusion phase lasted until the subject turned the knob clockwise by an additional angle, which we shall call the transport angle, which took the values 30°, 60°, and 90°. The gray arrow in Fig. 1b shows the subject’s possible mental representation of the invisible arrow’s orientation. Finally (Fig. 1c), the arrow reappeared briefly (the duration of one monitor frame, i.e., less than 13 msec, the decay time of P22 phosphor). The orientation of the flashed arrow was the ‘correct’ one (i.e., reflecting the subject’s motor rotation, including the rotation during the occlusion phase), plus an error term, which we will call the deviation angle. The deviation angle took the values ±10°, ±30°, ±50°, ±70°, with positive values signifying that the probe was shifted forward from its correct orientation (i.e., clockwise). The subject then stopped turning the knob and answered whether the probe arrow at the orientation of the flash was too far ahead or too far behind in its trajectory. Thus if the subject believed that the arrow should have been at the orientation shown by the gray arrow in Fig. 1c, rather than the orientation of the arrow actually flashed on the screen, the answer would have been in that case "too far ahead."
|
|
|
|
|
|
|
|
|
a. Initial visible phase |
b. Occlusion phase |
c. Flash and response |
Figure 1. Illustration of the three phases of Experiment 1. The top panel shows the visual stimulus, while the bottom panel shows the simultaneous manual action in the MOT condition. Only the black arrow was visible, while the gray arrow shows a subject’s possible estimate of the position.
The only difference between the visual and the motor trials was that in the visual trials the subject watched the arrow turn, instead of making it turn with the knob. The motor and visual trials were run in an alternating sequence. There were two types of visual trials, differing in how the spatio-temporal trajectory of the arrow was generated. In the replay trials (REP), the trajectory on the screen was the one generated by the subject on a previous, otherwise identical, MOT trial. In the linear trials (LIN), the trajectory of the preceding motor trial (of possibly different transport and deviation angles) was approximated by one of constant angular speed; the averaging was done starting from the moment the subject rotated the knob by more than 3°.
The experiment was run in 2 sessions of 3 blocks each, with 96 trials per block. Trials alternated between the active (MOT) and passive (REP, LIN) conditions. During the first half of each block, the passive trials were of the LIN type, in each of which the constant angular speed was calculated from the preceding MOT trial. In the second half of each block the passive trials were of the REP type, each of which duplicated the trajectory of a same-condition MOT trial from the first half of the block.
Results
Ten unpaid volunteers (5 men and 5 women, mean age 29 years) served as subjects. Subjects had normal or corrected-to-normal vision and no known motor deficits. All subjects were self-reported as right-handed, and used their right hand in the motor task. Subjects were naive as to the purpose of the experiment. After a practice block of 20 trials, each subject performed 576 trials in two 1-hour sessions.
Trials in which either the duration of the occlusion phase, the combined duration of the visible and occlusion phases, or the response time exceeded 10 sec were eliminated from further data analysis; 0.9% of all trials were thus eliminated.
Trajectories and timing
Before giving the results of the main prediction task, we shall briefly present the timing and trajectory details. In the active MOT trials subjects were free to perform the motor rotation at any speed, which resulted in variation in the durations of the different phases of the trial. The passive trials followed the MOT trials in mean angular speed (LIN) or trajectory (REP), so the variations in the active condition had an effect on the passive trials. Table 1 lists the mean durations of the initial visible and occlusion phases for the MOT and LIN trials (the REP trials are of course identical to MOT).
Table 1. Mean durations (sec) of the first two phases in the different conditions.
|
|
Condition |
Transport angle |
||
|
30° |
60° |
90° |
||
|
Initial visible phase |
MOT, REP |
0.58 |
0.57 |
0.58 |
|
LIN |
0.74 |
0.74 |
0.76 |
|
|
Occlusion phase |
MOT, REP |
0.50 |
1.02 |
1.64 |
|
LIN |
0.49 |
0.97 |
1.51 |
|
The trajectories in the MOT trials (and therefore in REP) typically consisted of an acceleration followed by a deceleration. Figure 2 partially illustrates the speed profile of these trajectories by showing the mean angular speed of motor rotation during the visible and occlusion phases, and the instantaneous speed (computed on the basis of an 80 msec interval) at the end of each of the two phases. As can be seen, the deceleration began around the start of the occlusion phase.
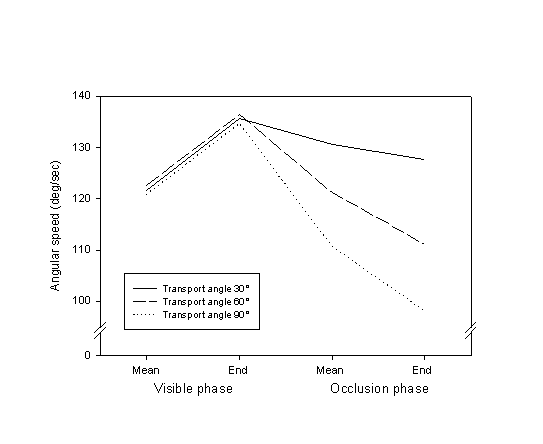
Figure 2. Mean motor rotation speeds at different phases of MOT trials.
Effect of movement condition and transport angle
We now turn to results of the prediction task. We can recover the subject’s estimate or prediction bias for the different transport angles by analyzing the response as a function of deviation angle. We will define the response in a given condition as a fraction of trials for that condition in which the subject responded that the probe was "too far advanced." Thus, for all the transport angles, the ideal result would be a response of 0 for negative deviation angles (for which the probe was shifted backwards from its true orientation), and 1 for positive ones (for which the probe was shifted forwards).
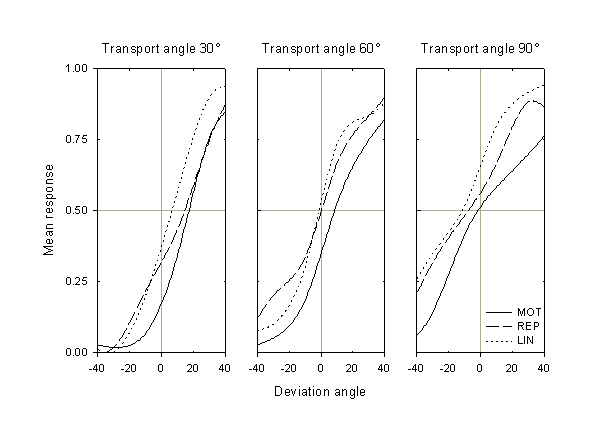
Figure 3. Mean response (fraction of responses that the probe was too far advanced) as a function of deviation angle from its true position, for the three transport angles and three conditions. Data are averaged over all subjects. All angles are in degrees, with positive angles in the direction of rotation (clockwise).
The mean response of the eleven subjects for the three transport angles and in the three conditions is shown in Fig. 3. We note several features of these data. First, for all three transport angles, the MOT curve is to the right of the REP curve, which is generally to the right of the LIN curve. This means that the subjects’ estimates of the position of the probe are farthest advanced in the active, MOT condition, and relatively retarded in the two passive conditions, REP and LIN. Second, in all three conditions the estimates become more retarded (i.e., the bias decreases) as the transport angle increases. Finally, and not unexpectedly, the width of the curves (i.e., the span of their transition regions) increases at larger transport angles; in other words, as the estimation duration, the responses become more variable.
To get a better handle on individual subjects’ biases, we perform a logit fit of the response as a function of deviation angle, separately for each combination of subject, motor and transport angle factors, and then average over subjects. Cases where either the absolute value of the bias or the width of the logit curve was greater than 100° were not used in subsequent analysis; in these cases, the logit parameters were presumably not reliable. Figure 4 shows the resulting mean displacement biases.
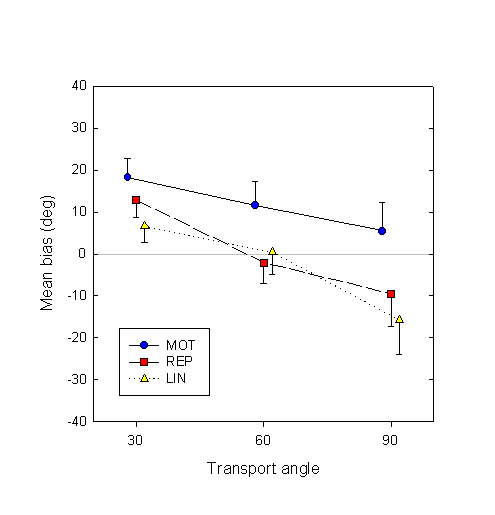
Figure 4. Estimation biases (in degrees), averaged over subjects, in the three conditions and at the three transport angles. Error bars show between-subject standard errors.
Figure 4 clearly confirms the above-mentioned trends: the MOT displacement estimates are farther advanced than those in the REP and LIN conditions, and all three decrease as transport angle increases.
The positive difference in bias between the active and passive conditions is quite robust, in that it is present in individual subject data. The difference in bias between the MOT and REP conditions, averaged over the three transport angles, is positive in all 10 out of 10 subjects. The MOT – LIN difference is positive in 9 out 10 subjects.
To further test the difference between active and passive conditions, we performed a movement condition (i.e., MOT, REP, LIN) x transport angle ANOVA on the above bias data. The two main effects are significant: F2,18 = 17.3, p < 0.01 for condition and F2,18 = 8.46, p < 0.01 for transport angle. The interaction between the condition and transport angle factors does not reach significance (F4,36 = 2.26, p = 0.08). However, the difference between the active and passive conditions, compared at the extreme values of 30° and 90° of the transport angle, does show significant effects: F1,9 = 5.00, p = 0.05 for MOT and REP, F1,9 = 8.51, p = 0.02 for MOT and LIN. In other words, the difference between the active MOT condition and the passive REP and LIN conditions increases as the estimation time rises.
Comparing the conditions in pairs, there is a significant difference between the MOT and REP conditions (F1,9 = 13.7, p < 0.01) and between MOT and LIN (F1,9 = 48.7, p < 0.01). On the other hand, the difference between the two passive conditions REP and LIN is not significant (F1,9 = 1.66, p = 0.23). Furthermore, the main effect of condition is separately significant for all transport angles, including the smallest angle of 30° (F2,18 = 7.17, p < 0.01). Analyzing the three movement conditions separately, we find that the decrease in bias as a function of the transport is significant in every condition (p < 0.01).
In addition to analyzing the relative effects of movement condition and transport angle on the biases, we can also compare the biases directly with their ideal value, viz. zero. Of the nine mean biases (three movement conditions by three transport angles: see Fig. 4), a t test shows that only two are statistically significant from zero: at transport angle 30°, the biases in both MOT and REP conditions are significantly positive (t9 = 3.95, p < 0.01 and t9 = 3.11, p = 0.01, respectively).
We also calculated the widths of the fitted response curves. The width is a measure of the variability of the subjects’ responses; sharp transitions between the two forced choices yield low widths, and vice versa. Performing an ANOVA on the widths similar to the one for biases, the only significant effect we find is of the transport angle: F2,18 = 17.2, p < 0.01. This effect can be seen from an inspection of Fig. 3, as a widening of the curves for larger transport angles. The increase in width is rather mild; comparing transport angles 30° and 90°, we have an increase of only 65%, which is small given the fact that the estimation interval (and presumably the task difficulty) increases by 200%. None of the other effects or interactions approaches statistical significance for the widths.
Effect of speed
In our protocol, subjects were free to rotate the knob at any speed they wished. We found, not surprisingly, that subjects often showed large variations in speed between trials. We wanted to check the effects of these spontaneous speed variations on the prediction task; in particular, we were interested in the effects of speed during the occlusion phase of the trial. To do so, in each condition (i.e., the trials for a given subject, movement condition and transport angle) we calculated the median of the mean motor speeds in the occlusion phase. We then subdivided the trials into two groups, depending on whether their mean speed fell above or below the median in their condition, thus introducing an additional categorical factor of speed. The mean angular motor speed during the occlusion phase was 44.0°/sec for the slow trials, 89.9°/sec for the fast trials. We then performed the analysis precisely as before (i.e., separate logit fits of mean response vs. deviation angle in each condition for each subject), but with the additional speed factor.
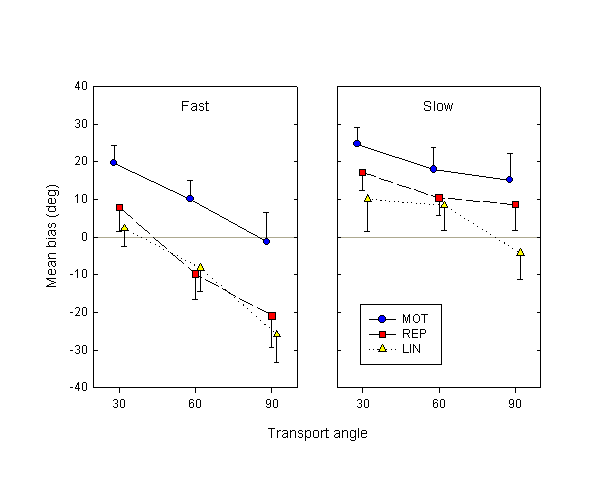
Figure 5. Mean bias over subjects as a function of condition and transport angle (as in Fig. 4), separately for the fast and slow trials.
Figure 5 shows the mean biases calculated for the fast and slow trials. A speed x movement condition x transport angle ANOVA on these biases reveals a significant main effect of speed (F1,9 = 64.7, p < 0.01): subjects’ estimates of probe displacement are farther advanced in the slow trials than in the fast trials. In other words, when the occlusion phase lasts longer but the actual displacement during that phase remains the same, estimates are more advanced. Furthermore, there is a significant interaction between the speed and transport angle factors (F2,18 = 13.3, p < 0.01), showing that the bias in the slow trials is significantly flatter as a function of transport angle that in the fast trials. The main effects of movement condition and transport angle remain significant.
In the fast trials, the difference between MOT and REP conditions is still statistically significant (F1,9 = 5.47, p < 0.05), while in the slow trials the difference is numerically reduced and approaches, though does not reach, significance (F1,9 = 4.13, p = 0.07). The MOT – LIN difference is significant in both fast (F1,9 = 27.3, p < 0.01) and slow (F1,9 = 10.7, p < 0.01) trials, while the REP – LIN difference is significant in neither (F1,9 = 0.93, p = 0.36 and F1,9 = 2.70, p = 0.13, respectively).
The effect of speed is quite robust, and exists in individual subject data. In the MOT condition, the difference in biases between the slow and fast conditions, averaged over the three transport angles, is positive in all 10 out of 10 subjects. In the passive REP and LIN conditions, this difference is positive in 9/10 subjects.
Performing a speed x movement condition x transport angle ANOVA on the widths, we find two significant effects, both involving the speed factor. First, there is a significant main effect of speed: for fast trials the mean width is 9.1°, for slow trials, 12.8° (F1,9 = 6.44, p = 0.03). Second, there is a significant interaction between the speed and the transport angle. For the fast trials, the width as a function of transport angle is flat (9.5° for transport angle 30°, 8.7° for transport angle 90°), whereas in the slow trials the width rises sharply with transport angle (9.0° for 30°, 16.5° for 90°) (F2,18 = 6.46, p < 0.01).
Discussion
There are three main results in this experiment: estimates of unseen target displacement are more advanced in the active condition than in the passive conditions; all estimates become more retarded as the occlusion distance increases, but estimates in the passive condition deteriorate faster; and slower rotations, i.e., longer occlusion periods, yield more advanced displacement estimates.
The main effect is the difference between the active MOT and passive REP conditions. Despite the fact that trajectories of the visual target were identical in the two conditions, the fact of acting on the target—rather than observing it passively—has a significant effect on the prediction of its trajectory. Namely, in otherwise identical conditions, the target is predicted to be farther advanced in the active condition than in the passive condition. This effect is not only significant in aggregate data, but is present in the individual data of all ten of our subjects.
At the smallest transport angle (30°), when the target’s trajectory has to be predicted over a period of about 500 msec on the average, predictions in all conditions are advanced (see Fig. 4). In other words, subjects are anticipating the true state of the target. But even here the bias in the active MOT condition (18.5° on the average) is ahead of the bias in the passive REP condition (12.8°). At the largest transport angle (90°), where the occlusion phase lasts 1.5 sec on the average, the mean MOT bias (5.5°) is still positive, though no longer significantly different from zero. The REP bias, on the other hand, is now negative (–9.5°): subjects are no longer anticipating the actual trajectory, but lagging behind. Biases in both the MOT and REP conditions decrease as the transport angle increases, i.e., displacement estimates lag further and further behind their initial anticipatory values. However, this decrease is less steep in the MOT than in the REP condition. Thus, an actual 60° difference in target displacement during the occlusion phase translates into a 47.0° advance of the mean displacement estimate in the active MOT condition, but only a 37.7° advance of the mean estimate in the passive REP condition. The transformation of the estimated target position is therefore more faithful to actual target motion in the active than in the passive condition.
The data in the MOT condition can be compared to the results of Wolpert et al. (1995), who studied the visual estimation of displacements of the hand. The main difference between their protocol and ours is the lack in Wolpert et al.’s protocol of an initial phase in which the displacement of the target was visible (though the subject saw the initial position before the onset of movement). Wolpert et al. found that subjects overestimated the unseen displacements, much as our subjects do in the MOT condition. Furthermore, these authors also found that the absolute amount of this overestimation declined with increase of the prediction time interval, which is compatible with our result that bias in the MOT condition decreases with larger transport angles, which are highly correlated with occlusion time.
The target speed during MOT and REP trials is not constant, due to the self-generated nature of the movements. The trajectory typically undergoes an acceleration followed by a deceleration that begins around the transition between the visible and occlusion phases (see Fig. 2). In order to test whether any of the effects that we found were due to the complex nature of the trajectories involved, we introduced a second passive condition, LIN, in which the mean speed of the target was the same as in the other conditions, but in which the target moved at a constant angular speed. From a formal point of view, at least, this should be the easiest type of trajectory to predict. We found no significant difference between the two passive conditions. It does not seem, therefore, that the complexity of the trajectories in the MOT and REP conditions is responsible for the effects that we have found. Furthermore, subjects are just as good at predicting the complex acceleration-deceleration trajectories in the REP condition as they are at predicting motion that is, mathematically, simplest of all: constant speed.
Another important effect that we have uncovered is that of speed. All other conditions being equal, faster rotations resulted in predictions of target position that were more retarded. In other words, when subjects had more time to predict, over the same prediction distance, the estimate was farther advanced. Moreover, the bias curves as a function of transport angle were significantly flatter for the slower trials than for faster the trials, implying that the rate of predicted advance of the target slowed down less for the slower than for the faster trials. Less surprisingly, the speed also has an important effect on the variance, or width, of the subjects’ replies: in the fast trials (i.e., ones where the target was hidden briefly), the width remains flat as a function of transport angle; in slow trials, it rises sharply. From this we may conclude that the subject’s uncertainty rises rapidly with the time duration of the prediction to be made.
The effect of speed in the passive conditions REP and LIN is comparable to the findings of Ellingstad (1967) and of Bonnet and Kolehmainen (1970) for passively observed linear motion. On the other hand, our results disagrees with those of Peterken et al. (1991), who found that longer prediction times over fixed prediction distances led to predictions that were more retarded.
Overall, it is clear that generating a movement (the MOT condition) effects the prediction of the movement’s outcome, as compared to passively observing a movement (the REP and LIN conditions): in the active case the prediction is more anticipatory than in the passive case.
Experiment 2
In Experiment 1, the motor action in the MOT condition was a rotation, and so was the visual motion to be predicted. We now ask to what extent is this action-prediction effect intermodal. Does a motor rotation advance predictions only of congruent visual motion, namely visual rotation, or is the interaction more general and thus higher-level, so that the performance of a motor action in general advances the prediction of the action’s visual outcome, regardless of the specific forms of the action and visual feedback?
Experiment 2 addresses this question. The major modification with respect to Experiment 1 is that visual feedback is no longer a rotation of an arrow on the screen, but a translation. The motor action, in the active condition, has not been changed: it is still a rotation.
Another goal of Experiment 2 is to probe for the role of eye movements in the prediction task. As discussed in the Introduction, eye movements are themselves predictive; this predictive capacity could be effected by the manual task (or lack thereof), and it could in turn effect the subject’s performance of the predictive task. In Experiment 1, subjects had no explicit instructions concerning eye movement. In Experiment 2, trials were either pursuit, in which subjects were instructed to follow the moving arrow with their eyes and to continue the ocular pursuit as much as possible even in the occlusion phase, after the target disappears; or fixation, in which the subjects were to fix a cross on the screen at all times. Otherwise, all other experimental conditions in Experiment 2 were very similar to those in Experiment 1.
Method
The subject’s manual movement in the MOT trials consisted in a rotation of a knob, as in Experiment 1. The visual feedback, however, was no longer a rotation but a translation. A vertical, upward-pointing arrow (otherwise identical in shape and size to the arrow in Experiment 1) always began near the left edge of the screen on each trial. The arrow’s subsequent movement was a translation to the right. On the MOT trials, the visuomotor gain was 10.8°/cm; in other words, for every 10.8° the subject rotated the knob, the arrow moved to the right by 1 cm.
In contrast to Experiment 1, subjects had explicit eye movement instructions. On half of the trials ("pursuit"), subjects were told follow the arrow with their eyes as it moved to the right, and to continue the visual pursuit as best as possible after the arrow disappeared. On the other half of the trials ("fixation"), a red fixation cross was drawn on the screen throughout the trial (1.2 cm long, centered at 3.5 cm above the tip of the arrow, 9.7 cm to the right of its initial position, corresponding to the horizontal position of the arrow following a motor rotation of 105°, or 60° after the onset of the occlusion phase), and the subject was instructed to fixate the cross throughout the trial. The experiment was run in two sessions of 288 trials each. One session had pursuit and the other had fixation trials; otherwise, the two sessions were identical. The order of the pursuit and fixation sessions was counterbalanced across subjects.
|
|
|
|
|
|
|
|
|
a. Initial hidden phase |
b. Occlusion phase |
c. Flash and response |
Figure 6. Illustration of the three phases of Experiment 2. The top panel shows the visual stimulus, while the bottom panel shows the simultaneous manual action in the MOT condition. The black arrow represents the actual visual stimulus, while the gray arrow shows the subject’s possible estimate for the target position.
Results
Eight unpaid volunteers served as subjects. Group 1 (2 men, 2 women, mean age 29 years) performed fixation trials in the first session, followed by pursuit trials in the second session. Group 2 (3 men, 1 woman, mean age 24 years) performed pursuit trials in the first session, followed by fixation trials. All subjects were self-reported as right-handed, and used their right hand in the motor task. Subjects were naive as to the purpose of the experiment.
Trials in which either the duration of the occlusion phase, the combined duration of the visible and occlusion phases, or the response time exceeded 10 sec were eliminated from further data analysis; 2.3% of all trials were thus eliminated.
Effect of eye tracking and movement condition
The analysis that we performed was similar to that for Experiment 1. Briefly, data were categorized by subject, fixation condition, movement condition and transport angle. In each cell, mean response as a function of deviation was fitted to a logit curve. The resulting mean biases are shown in Fig. 7, the counterpart of the data in Fig. 4, but additionally categorized by eye movement condition. Although the visual motion here is a translation, to facilitate comparison with Experiment 1 displacements are given in degrees (recall that the visuomotor gain is 10.8°/cm).
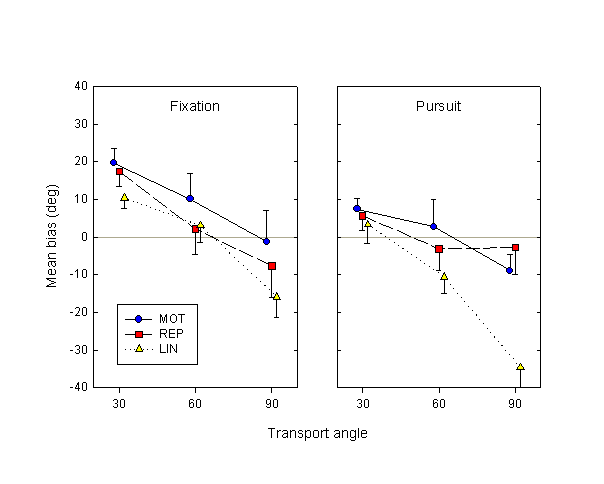
Figure 7. Mean biases in Experiment 2, as a function of eye movement, movement condition and transport angle.
The results in the fixation condition in this experiment closely resemble those of Experiment 1 (see Fig. 4). There is a significant effect of transport angle (F2,14 = 18.3, p < 0.01), and a difference between the active MOT and passive REP and LIN conditions that approaches significance (F2,14 = 3.02, p = 0.08). The latter difference is similar to the one in Experiment 1, but is smaller in magnitude.
In the pursuit condition, on the other hand, all difference between the MOT and REP conditions disappears (F1,6 = 0.19, p = 0.67). There is, however, a significant difference between these two conditions and the LIN condition (F1,6 = 11.1, p = 0.02), as well as a strong interaction between movement condition and transport angle (F4,24 = 4.30, p < 0.01), due to the much faster decrease of LIN bias as a function of transport angle than in the MOT and REP conditions.
Comparing active and passive conditions for individual subjects, we find that in the fixation condition, MOT estimates are more advanced (anticipatory) than REP in 7 out of 8 subjects; MOT estimates are more advanced than LIN bias in 6/8 subjects. In the pursuit condition, MOT estimates are more advanced than REP bias in half the subjects, while estimates are more advanced than LIN bias in all 8/8 subjects.
Comparing the fixation and the pursuit conditions, we find that the mean effect of tracking is to retard displacement estimates. The mean bias in the fixation condition is 2.7°, while in the pursuit condition it is –7.2°; this effect approaches significance (F1,6 = 4.97, p = 0.07). An alternative measure of the robustness of the effect of eye movement is afforded by individual subject data. In the MOT condition, the biases for 7 out of 8 subjects (averaged over transport angle) were more advanced in the fixation than in the pursuit condition. In the passive conditions, the corresponding figure was 5/8 for REP and 6/8 for LIN.
Effect of speed
To check the effect of movement speed, we categorize trials into fast and slow groups, as in Experiment 1 (based on mean speed during the occlusion phase). Figure 8 shows the mean biases for the MOT, REP and LIN conditions, categorized by speed and eye movement condition; the data are averaged over subject and over transport angle. The effect of speed is similar to that in Experiment 1: in every condition, the estimates in slow trials are farther advanced, more anticipatory than in fast trials. Performing a four-way ANOVA by eye tracking condition, movement condition, transport angle and speed, we find a significant main effect of speed: for the fast trials the mean bias is –5.6°, for the slow trials it is 3.4° (F1,6 = 12.0, p = 0.01). The effect of fixation is in the opposite direction as that of speed: in every case, the mean estimate for fixation trials is farther advanced than for pursuit trials.
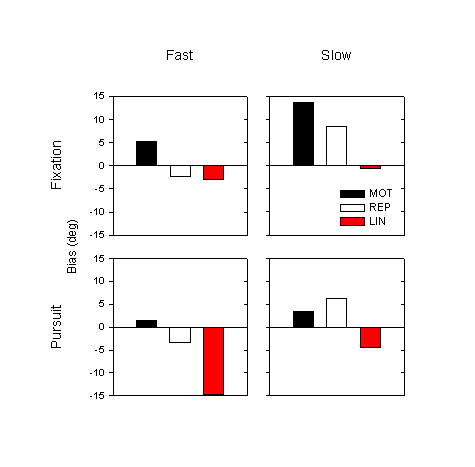
Figure 8. Mean bias (over subjects and transport angles) for the three conditions, categorized by speed and by eye movement condition.
Comparison of Experiments 1 and 2
In Experiment 1 both the motor action and the visual feedback were rotations; in Experiment 2 the motor action was still a rotation, but the visual feedback was a translation. To what does the mismatch between motor action and feedback effect the prediction task?
It is clear from a comparison of Fig. 4 and Fig. 7 that Experiment 1 and the fixation condition of Experiment 2 closely resemble one another, whereas the pursuit condition of Experiment 2 has yields estimates that are generally more retarded than the two others. Indeed, if we perform an ANOVA with experiment as a between-groups factor (three levels: Experiment 1, Experiment 2 fixation, Experiment 3 pursuit), and movement condition (MOT, REP, LIN) and transport angle as within-subjects factors, we find no significant differences whatsoever between Experiment 1 and Experiment 2 fixation. On the other hand, there is a significant difference between these two and Experiment 2 pursuit, but only in the LIN condition (F1,22 = 5.14, p < 0.05), while the same difference in the MOT condition approaches significance (F1,22 = 3.42, p = 0.08).
The effect of motor action is quantified by the difference in bias between the active and the two passive conditions (MOT – REP and MOT – LIN). Does the congruence of motor and visual movement (Experiment 1 vs. 2) or the eye movement condition modulate this effect? Figure 9 shows these two bias differences for Experiment 1 and Experiment 2, fixation and pursuit. For the MOT – REP, the pattern is clear: the bias difference is greatest for Experiment 1, smaller for Experiment 2 fixation, and smaller still (even negative at large transport angles) for Experiment 2 pursuit. Moreover, these effects seem to increase with increasing transport angle. The difference between Experiment 1 and Experiment 2 fixation fails to achieve significance, though (F1,22 = 1.89, p = 0.18). On the other hand, the difference between Experiment 1 and Experiment 2 pursuit is significant (F1,22 = 5.10, p < 0.05), and its interaction with transport angle is significant as well (F1,22 = 6.51, p < 0.05).
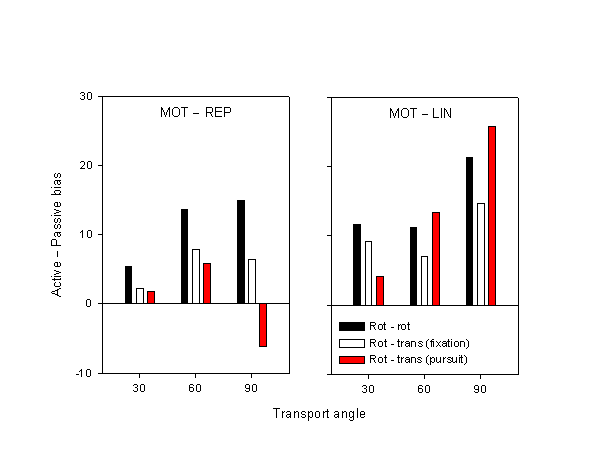
Figure 9. Differences between the active and the two passive conditions, viz. between MOT and REP and between MOT and LIN. Data are shown for Experiment 1 (motor rotation – visual rotation) and the ocular pursuit and fixation conditions of Experiment 2 (motor rotation – visual translation). Error bars represent between-subject standard error.
Discussion
In this experiment we have modified the congruence of motor action and visual feedback: the action is a rotation while the feedback is a translation. We have also controlled eye movement by introducing ocular pursuit and fixation conditions.
We have found that the fixation condition of Experiment 2 closely resembled the results of Experiment 1. The principal effect of movement condition from Experiment 1—the fact that displacement estimates in the MOT condition are more advanced or anticipatory than in the passive REP condition—has been reduced in magnitude relative to Experiment 1, but not eliminated. The resemblance of the results of the fixation conditions to those of Experiment 1 is not surprising: in Experiment 1, the visual stimulus underwent a rotation; subjects could have tracked the tip of the rotating arrow with their eyes, but as such tracking is not very natural and was not required, it is unlikely that subjects did so, or at least systematically. If subjects did have consistent eye movements, more probably they fixated the center of the rotating arrow. Therefore, the fixation condition of Experiment 2 is naturally closer to Experiment 1. There was a trend for the MOT – REP difference in Experiment 2 fixation to be smaller than that in Experiment 1, though this difference is not statistically significant. We conclude, therefore, that the partial motor-visual mismatch introduced in Experiment 2 did not eliminate the action effect (but did possibly reduce it), given comparable eye movement conditions.
The effect of ocular pursuit, as compared to the fixation condition, is triple: to retard displacement estimates; to nullify the difference between the active MOT and passive REP conditions; and to retard the estimates in the LIN condition, creating a significant difference between the two passive conditions, REP and LIN. It appears that the lack of manual action in the REP condition is compensated by ocular pursuit, erasing the difference between MOT and REP. The LIN condition, on the other hand, has extremely retarded displacement estimates, especially for large transport angles; this should be contrasted with Experiment 1 data, and those from the pursuit condition of Experiment 2, where there is no difference between the two passive conditions. The gap between REP and LIN in the pursuit condition agrees with the fact that ocular pursuit soon slows down and tapers off in the absence of a visible target (Barnes and Asselman, 1992) Trajectories in the REP condition already have a deceleration during the occlusion phase, due to their ‘biological’ nature, and this is possibly why the REP predictions are less delayed than those for the constant-speed LIN trajectories. It is also worth comparing this result with the finding of de’Sperati and Viviani (1997) that passively observed ‘biological’ trajectories, such as those in the REP condition, are easier to track than trajectories following other velocity profiles.
Finally, we have reproduced the effect of speed that had been found in Experiment 1. Targets taking longer to traverse a given distance, and therefore moving slower, yield predictions that are farther advanced than the faster-moving, shorter-duration targets. This is true in all three conditions (MOT, REP, LIN).
General Discussion
Our findings
The chief effect that we have demonstrated is the difference in displacement estimates between the active (MOT) and passive (REP, LIN) conditions. Before discussing the differences between the conditions, however, it is instructive to first ponder their similarities. Of these there are at least two. Of the differences between active and passive conditions, the most important is the fact that predictions in active trials are farther advanced—more anticipatory—than in passive trials, even when temporal trajectories are rigorously identical, as they are in MOT and REP conditions. This effect is stronger when motor action and visual motion are congruent (as they are in Experiment 1, where they were both rotations, versus Experiment 2, where the action is a rotation but the visual motion a translation), and stronger for fast trials than for slow trials. The effect is also modulated by eye movement: it is present in Experiment 1 (where subjects were unlikely to have tracked the visual target with their eyes, due to its rotation) and the fixation condition of Experiment 2; on the other hand, it is absent in the tracking condition of Experiment 2. All of these effects are quite robust, and found on the level of individual data. Further, there is some evidence of an interaction between movement condition and prediction distance: the slowing down of the predicted position as a function of prediction distance seems to be less steep in the active than in the passive case.
Along with the differences in prediction between the active and passive conditions, we have also found at least two interesting similarities. First, as the prediction distance (the displacement over which the target is occluded) increases, predicted displacements lag farther and farther behind. This is true of both active and passive tasks, although there is evidence, especially from Experiment 1, that this slowing down is steeper in passive than in active trials. Second, for a given prediction distance, slower movements result in predictions that are farther advanced than do faster movements. This is also true of both active and passive conditions; here, the magnitude of the effect seems to be roughly the same for passive as for active conditions. These two effects were found in both Experiments 1 and 2, and are individually present in either a vast majority or in all subjects.
The fact that active prediction remains more anticipatory than passive ones, even when visual feedback is less congruent to the motor action (as it is in Experiment 2, relative to Experiment 1), shows that the effect of motor action on prediction is not tied to the low-level details of the produced movement and the visual stimulus, but suggests the intervention of more general, high-level mechanisms that adaptively predict the outcome of motor action, mechanisms that continue to operate even when visual motion and motor action are geometrically dissimilar. It is interesting to compare this result to the neurophysiological data of Eskandar and Assad (1999), who have found a population of cells in the posterior parietal cortex of macaques that predictively encode the unseen visual trajectories of targets that are being moved by the animal, but where the motor action and visual feedback motion are partly incongruent: they are both translations, but in orthogonal directions.
One obvious difference between the active MOT condition, and the passive REP condition is, despite the identical trajectories, the lack in the REP condition of any direct information (efferent copy of movement commands, proprioception) about the movement of the target in the occlusion phase. If, as far as prediction is concerned, this were the only difference between the two conditions, we would not expect any systematic difference in the mean estimates, but rather for the passive responses to be less precise than the active ones. This is, in fact, not the case: if anything, REP widths (a measure of precision) are smaller than MOT widths, and there is a systematic difference in mean estimates, namely that MOT estimates are more advanced. We conclude, therefore, that our effects cannot be explained solely by the lack of movement information in the passive conditions.
Finally, there is an effect of eye movements on the prediction task. Pursuit eye movements retard prediction in both active and passive conditions; in the presence of such eye movements, the difference between the active MOT condition and the passive REP condition (where the trajectories are identical) disappears. However, with ocular pursuit a gap appears between the two passive conditions REP (where the kinematics is ‘biological’) and LIN (where the speed is constant). This is possibly related to the slowing down of smooth ocular pursuit after the disappearance of a visual target (Barnes and Asselman, 1992).
Possible mechanisms
What can we conclude about the neural mechanisms underlying active and passive prediction? A crucial choice has to be made at the outset: does trajectory prediction in the passive case share any mechanisms with the active case? Given the parallels that we have found between the dynamics in the active and passive cases (similar decay of subjective speed with occlusion interval, similar effect of target speed), we will assume that at least some of the mechanisms responsible for active and passive prediction are the same. These parallels are suggestive, however; most probably, the matter will only be settled by neurophysiological or neuropsychological techniques.
Given our assumption of a common neural mechanism underlying both active and passive prediction, what sort of a model could parsimoniously account for both the similarities and the differences in the two cases? First off, we shall need a representation of current target configuration (i.e., the significant degree(s) of freedom, such as the angle in Experiment 1 or linear position in Experiment 2), that we shall call the store. The same store could represent both observed target configuration, when the target is visible, or estimated target configuration during periods of occlusion. An attractive medium for such a store would be a population of neurons such as the one in monkey motor cortex studied by Georgopoulos et al. (1989), where each cell is tuned to a particular direction of arm movement and where the average direction over the population, weighted by the cells’ activations, is a ‘population vector’ that represents the actual direction of movement. The population vector is not merely a static representation but can rotate from one direction to another in response to task demands (Georgopoulos et al., 1989). It is not known, however, whether the rotation of the population vector is dynamical property of that particular group of cells, or if the change in the population vector represents the outcome of a process that takes place elsewhere. It cannot be excluded, however, that a population vector have intrinsic dynamical properties that would allow it to rotate itself, much as the ‘dynamical memory’ introduced by Droulez (Droulez and Berthoz, 1990).
There is indirect evidence that a similar population vector representation mediates human visuomotor and visual image transformations. Georgopoulos and Massey (1987) found that the time for a human subject to initiate an arm movement that is offset by an angle from a stimulus orientation is linearly dependent on the offset angle, much as it is in the monkey, where during the initiation time the population rotates by the offset angle. Pellizzer and Georgopoulos (1993) found that individual human subjects’ movement initiation times in the visuomotor task were closely correlated to response times in mental rotation of visual images, more so than to RTs in other tasks. This suggests that a population vector code may be employed for visuomotor tasks in humans, and that an overlapping representational mechanism may underlie ‘purely visual’ tasks, i.e., ones without an overt motor component. There is no reason to suppose that such population-based representations be confined to motor or visual rotation; they could equally well represent translation, or other types of movement.
The crucial feature of a predictive store is updating: based either on efferent copy of the motor command or proprioceptive information or on past visual trajectory (in the active case) or on past visual information alone (in the passive case), the store must be continually updated to reflect the estimate of the current configuration. In the active case, the store could be updated by means of a forward model, such as the Kalman filter models of Wolpert and Miall, or the ANN model of Droulez, that predict future state based on efferent copy of motor commands. In our experiments, for instance, during the initial visible phase, the store’s time evolution reflects the movement of the perceived visual target. During the occlusion phase, the store’s evolution is an integration of the estimated effects of current motor commands.
In the passive case, where movement-command or proprioceptive information is not available, we can imagine two scenarios for updating. First, the store could have intrinsic dynamic properties. Having undergone a time evolution during the visible phase that simply reflects the target’s seen motion, the store’s dynamics may feature an effective ‘momentum’ (cf. Freyd, 1987), so that the it continues to evolve after the target is occluded. The speed at which the store evolves during occlusion may not match the visible target speed, and may change over the occlusion period. In light of our results, the transfer function between the visible speed and the predicted speed may be a low-pass filter, which would account for the finding that predictions of high-speed trajectories are delayed as compared to low-speed trajectories. Thus the initial speed of evolution during the predictive phase may already be some non-trivial function of the speed during the visible phase. Furthermore, this initial speed subsequently slows down, as demonstrated by our finding that predictions become more retarded for longer prediction distances.
An alternative mechanism in the case of passive prediction could be termed ‘motor simulation’. During the visible phase, the subject could somehow evolve a simulated motor command that, if applied to the target, would reproduce the observed motion. Since no overt movement is produced, this motor activation would have to be inhibited from descending to the spinal chord and the periphery, much as in the case of motor imagery (e.g., Jeannerod, 1997). The construction of such a ‘reproductive motor simulation’ is rendered more plausible by analogous properties of ‘mirror neurons’ in monkey frontal cortex (Di Pellegrino et al., 1992), which reproduce the motor commands necessary to execute movements observed in another animal. Similar mechanisms probably exist in humans (Fadiga et al., 1995). When the target disappears and its trajectory is predicted, the simulated motor command could lead to the time evolution of the predicted target position through the same forward-model mechanisms that are used in the active case. The effect of the simulated motor command on the representation of target configuration may be weaker than the effect of the re-afferent copy of an actual motor command, which would account for the constant bias difference between the active and passive conditions that we have found. In the absence of overt motor action or of visual information, this simulated motor command would decay, explaining the steeper decrease of the bias as a function of prediction distance in the passive case than in the active case.
These two candidate mechanisms for passive prediction are not mutually exclusive. It could very well be that the first—representational momentum—acts only over short periods (cf. Freyd 1987), while the second mechanism—motor simulation—would act over longer periods. Now, representational momentum has been found to decay rather quickly. Therefore, a combination of a short-term representational momentum process and a longer-term motor simulation process could explain the speed effect, in which brief occlusions lead to predictions that are farther delayed than longer occlusions.
The mechanisms responsible for passive prediction could also play a role in the active case, of course. Yet the consistent differences that we find between predictions in the two cases lead us to suppose that the additional information present in the active case—most likely an efferent copy of the motor command—gives rise to more anticipatory predictions of the target, as compared to the processes in passive prediction. The active/passive differences that we have found are in line with theories of the predictive nature of movement, and, indeed, with the neurological evidence for anticipatory properties of neural mechanisms of movement. Nevertheless, the similarities between the predictive dynamics in the visuomotor and purely visual conditions provide strong evidence for at least some mechanisms that are common to active and passive prediction of movement.
Acknowledgement
We are grateful to Jacques Droulez for his suggestions and encouragement.
References
Barnes GR, and Asselman PT (1992) Pursuit of intermittently illuminated moving targets in the human. J Physiol (Lond) 445: 617-637.
Beutter BR, and Stone LS (1998) Human motion perception and smooth eye movements show similar directional biases for elongated apertures. Vision Res 38: 1273-1286.
Blakemore S-J, Wolpert DM, Frith, CD (1998). Central cancellation of self-produced tickle sensation. Nature Neurosci. 1: 635–640.
Bonnet C, Kolehmainen K (1970). Le rôle de la vitesse dans l’anticipation d’un mouvement visuel. Année Psychol. 70: 357–367.
Cai RH, Pouget A, Schlag-Rey M, and Schlag J (1997) Perceived geometrical relationships affected by eye-movement signals. Nature 386: 601-604.
de’Sperati C, and Viviani P (1997) The relationship between curvature and velocity in two-dimensional smooth pursuit eye movements. J Neurosci 17: 3932-3945.
Di Pellegrino G, Fadiga L, Fogassi L, Gallese V, and Rizzolatti G (1992) Understanding motor events: a neurophysiological study. Exp Brain Res 91: 176-180.
Droulez J, Berthoz A (1991). A neural network model of sensoritopic maps with predictive short-term properties. Proc. Natl. Acad. Sci. USA 88: 9653–9657.
Duhamel J-R, Colby CL, Goldberg ME (1992). The updating of the representation of visual space in parietal cortex by intended eye movements. Science 255: 90–92.
Ellingstad VS (1967). Velocity estimation for briefly displayed targets. Perceptual and Motor Skills 24: 943–947.
Eskandar EN, Assad, JA (1999). Dissociation of visual, motor and predictive signals in parietal cortex during visual guidance. Nature Neurosci. 2: 88–93.
Fadiga L, Fogassi L, Pavesi G, and Rizzolatti G (1995) Motor facilitation during action observation: a magnetic stimulation study. J Neurophysiol 73: 2608-2611.
Freyd JJ (1987). Dynamic mental representations. Psychol. Rev. 94: 427-438.
Georgopoulos AP, Kalaska JF, Crutcher MD, Caminiti R, Massey JT (1983). The representation of movement direction in the motor cortex: single cell and population studies. In: Edelman GM, Gall WE, Cowan WM (eds.), Dynamic aspects of neocortical function. Wiley, New York, pp. 501–524.
Georgopoulos AP, Massey JT (1987). Cognitive spatial-motor processes. The making of movements at various angles from a stimulus direction. Exp. Brain Res. 65: 361–370.
Georgopoulos AP, Lurito JT, Petrides M, Schwartz AB, Massey JT (1989). Mental rotation of the neuronal population vector. Science 243: 234–236.
Haarmeier T, Thier P, Repnow M, and Petersen D (1997) False perception of motion in a patient who cannot compensate for eye movements. Nature 389: 849-852.
Helmholtz H von (1866). Handbuch der physiologischen Optik, Bd. 3 Leipzig: Voss.
Holst E von and Mittelstaedt H (1950). Das Reafferenzprinzip. Naturwissenschaften 37, 464-476.
Jeannerod, M (1997). The cognitive neuroscience of action. Oxford: Blackwell.
Kowler E, and McKee SP (1987). Sensitivity of smooth eye movement to small differences in target velocity. Vision Res 27: 993-1015.
Müsseler J, and Aschersleben G (1998). Localizing the first position of a moving stimulus: the Fröhlich effect and an attention-shifting explanation. Percept. Psychophys. 60: 683-695.
O'Keefe, J, & Recce, ML (1993). Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus, 3: 317-330.
Pellizzer G, Georgopoulos AP (1993). Common preocessing constraints for visuomotor and visual mental rotations. Exp. Brain Res. 93: 165–172.
Peterken C, Brown B, Bowman K (1991). Predicting the future position of a moving target. Percpetion 20: 5–16.
Post RB, and Leibowitz HW (1985) A revised analysis of the role of efference in motion perception. Perception 14: 631-643.
Rieser JJ, Guth DA, Hill, EW (1986). Sensitivity to perspective structure while walking without vision. Perception 15: 173–188.
Rosenbaum, DA (1975). Perception and extrapolation of velocity and acceleration. J. Exp. Psychol. [Hum Percept Perf] 1: 395-403.
Slater-Hammel AT (1955). Estimation of movement as a function of the distance of movement perception and target distance. Perceptual and Motor Skills 5: 201–204.
Soechting JF, Flanders M (1989). Sensorimotor representations for pointing to targets in three-dimensional space. J. Neurophys. 62: 582–594.
Sperry, RW (1950). Neural basis of the spontaneous optokinetic response produced by visual inversion. J. Comp. Physiol. Psychol. 43, 482-489.
Steinbach MJ, and Held R (1968) Eye tracking of observer-generated target movements. Science 161: 187-188.
Wexler M, Kosslyn SM, Berthoz A (1998). Motor processes in mental rotation. Cognition 68: 77–94.
Wolpert DM, Ghahramani Z, Jordan MI (1995). An internal model for sensorimotor integration. Science 269: 1880–1882.
Wolpert DM, Goodbody SJ, Husain M (1998). Maintaining internal representations: the role of the human superior parietal lobe. Nature Neurosci. 1: 529–533.