In this paper we will outline one of the methods that we investigated for learning occlusion relations. Other methods may work as well.
Our method involves extending the EXIN (excitatory+inhibitory) learning scheme described by Marshall [10,11]. The EXIN scheme uses a variant of a Hebbian rule to govern learning in the bottom-up and time-delayed lateral excitatory connections, plus an anti-Hebbian rule to govern learning in the lateral inhibitory connections.
We extend the EXIN rules by letting inhibitory connections transmit disinhibitory signals under certain regulated conditions. The disinhibitory signals produce an excitatory effect at their target neurons.
Our new disinhibition rule specifies that when a neuron has strong, active lateral excitatory input connections and strong but inactive bottom-up input connections, then it tends to emit disinhibitory signals along its output inhibitory connections. The disinhibitory signals tend to excite the recipient neurons and enable them to learn. The disinhibition rule can be expressed as a differential equation governing neuron activation and implemented in a computational simulation.
During continuous motion sequences, without occlusion or disocclusion, the system operates similarly to a system with the standard EXIN learning rules: lateral excitatory ``chains'' of connections are learned across sequences of neurons along a motion trajectory. A moving visual object activates neurons along a chain; each activated neuron transmits predictive lateral excitatory connections to other neurons farther along the chain.
However, during occlusion events, some predictive lateral excitatory signals reach neurons that have strong but inactive bottom-up excitatory connections. When this occurs, the new disinhibition rule comes into play. The neurons reached by this excitation pattern emit disinhibitory rather than inhibitory signals along their output inhibitory connections. There then exists a neuron that receives a larger amount of disinhibition combined with lateral excitation than other neurons. That neuron becomes more active than other neurons and begins to suppress the activity of the other neurons via lateral inhibition.
In other words, a neuron that represents a visible object causes some other neuron to learn to represent the object when the object becomes invisible. Thus, the representations of visible objects are protected from erosion by occlusion events. Moreover, the representations of invisible objects are allowed to develop only to the extent that the neurons representing visible objects explicitly disclaim the ``right'' to represent the objects. These properties prevent the network from losing contact with actual bottom-up visual input and thereby help it avoid the hallucination problem.
Our system initially contains a homogeneous stage of neurons that receive motion input signals from prior stages. When the system is exposed to many motion sequences containing occlusion and disocclusion events, the stage gradually undergoes a self-organized bifurcation into two distinct pools of neurons, as shown in Figure 4. These pools consist of two parallel opponent channels or ``chains'' of lateral excitatory connections for every resolvable motion trajectory. One channel, the ``On'' chain or ``visible'' chain, is activated when a moving stimulus is visible. The other channel, the ``Off'' chain or ``invisible'' chain, is activated when a formerly visible stimulus becomes invisible, usually due to occlusion. The bifurcation may be analogous to the activity-dependent stratification of cat retinal ganglion cells into separate On and Off layers, found by Bodnarenko and Chalupa [3].
The On chain (Class I neurons) carries a predictive modal representation of the visible stimulus. The Off chain (Class II neurons) carries a persistent, amodal representation that predicts the motion of the invisible stimulus. The shading of the neurons in Figure 4 shows the neuron activations during an occlusion--disocclusion sequence. This network does not contain Class III neurons; instead, the Class I neurons respond to the unpredicted appearance of moving objects.
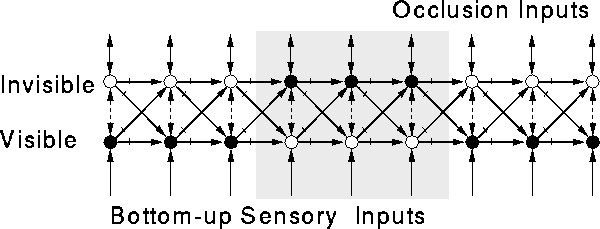
Figure 4: Network architecture after learning.
The learning procedure causes the representation of each trajectory to
split into two parallel opponent channels. The Visible and Invisible
channel pair for a single trajectory are shown. Solid arrows indicate
excitatory connections. Hash marks indicate time-delayed connections.
Broken arrows indicate inhibitory connections. The network's
responses to an occlusion--disocclusion sequence are shown. A visual
object (not shown) moves rightward along the trajectory. The object
is represented successively at each moment by neuron activations in
the Visible channel. (Solid circles represent active neurons; open
circles represent inactive neurons.) When the object reaches the
region indicated by gray shading, it disappears behind an occluder.
The network responds by successively activating neurons in the
Invisible channel. These neuron activations amodally represent the
network's inference that the object continues to exist and continues
to move while it is invisible. When the object emerges from behind
the occluder (end of gray shading), it is again represented by
activation in the Visible channel. Because the Visible and Invisible
channels are distinct, the neurons in the Invisible channel can also
learn bidirectional associations (reciprocal excitatory connections)
with other neurons whose activation is correlated with the presence of
an invisible object. If any such neurons exist, we can call them
occlusion indicators.
The network generates many predictions at every moment; each prediction's weight is determined partially by its learned statistical likelihood. Each prediction generated by the system has one of three possible outcomes: (1) an object appears at the predicted location; (2) an object does not appear at the predicted location but does appear at another predicted location; or (3) no object appears at a predicted location. The disinhibition rules ensure that one of these three outcomes is attributed to every prediction.