Software and Specifications
This Page will give an overview of how the software fits together (see figure 1) and the specification of the Custom operator required to integrate QTI with a Computer Algebra System (CAS).
Specifications for the “MathsContent” variable, customOperators and customInteraction –
MathAssess-specifications.pdf version
MathAssess-specifications .doc version
Workshop June 2009
In June 2009 we gave a series of workshops, a worksheet showing how to create question and tests was written.
The worksheet can be found here
List of software components.
J-Assess
SnuggleTex, ASCIIMathML and interconversion of mathematical formats
Mathqurate
MiniBix
QTIEngine, JQTI & Validatr,
Test Constructr
Moodel Plug-in
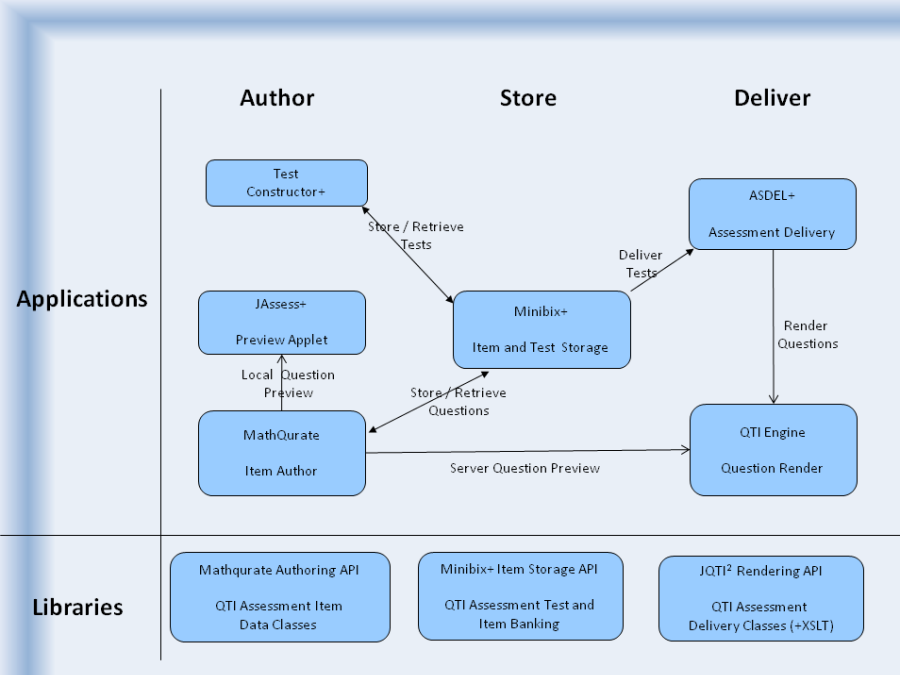
MathAssess tools; interactions
Although the existing toolkits for e-assessment had been developed and proven in earlier JISC projects, it was clear from the outset that significant enhancements of each would be required. The opportunity was also taken to improve and clarify the structure of their interactions with each other and with the user. Figure 1 shows the final outcome of this; details of the individual components follow.
MathAssess tools: MathQurate
MathQurate, the item authoring subsystem, is a re-implementation of AQuRate with the following new features:
- New interface based upon Eclipse
- Uses Java API for XML binding (JAXB)
- Uses JQTI2 library (see below) for preview
- Question features:
- Templates and randomisation
- Mathematical input via LaTeX
- customOperator for CAS computations
- customInteraction for mathematical input
This supports step-by-step authoring of an item as follows:
- 1. Create a new question or import an existing one
- 2. Review and edit metadata
- 3. Declare template and outcome variables
- 4. Declare the response variables
- 5. Edit the item body
- 6. Edit MathML, including support for re-editing and using SnuggleTex approach
- a. LaTeX input
- b. MathML output
- 7. Editing choice interactions to break up XML into digestible information by including
- a. Metadata editor
- b. HTML and MathML Prompt editor
- c. List of simple choices
- 8. Editing simple choices; these can contain HTML and MathML so requires metadata editing. This function is particularly important for mathematics as it allows editing of feedback provided to the student inline when this choice is selected.
- ...More Information
MathAssess tools: JQTI and Validatr
JQTI2 is a newly-released pure Java library developed from JQTI as part of MathAssess. The new version brings many improvements to the handling of QTI assessments and reports, most importantly a complete QTI item implementation with a full content model. JQTI contains everything required to read, write, validate and process (processing of templates, responses and outcomes are all fully supported) QTI items and assessments. Validatr is a graphical tool for examining and validating QTI content. Validatr can quickly show the locations of problems and issues that are impossible to locate using an xml schema validation. The capabilities of JQTI are such that no changes are required for MathAssess CAS support; the necessary functionality is provided by a plug-in library that just needs to be placed on the classpath.
MathAssess tools: Test Constructr
Test Constructr extends the proof of concept within the original Contructr from the ASDEL project to include these new features:
- •Uses improved JQTI library
- Take items from Minibix using the Maths taxonomy
- Package as test and deposit back into Minibix
...More Information on Constructr
MathAssess tools: QTIEngine
QTIEngine is a new open source engine developed within MathAssess for playing IMS QTI v2.0 and 2.1 content. QTIEngine utilises JQTI 2 to handle QTI xml, and uses a completely customisable XSLT-based rendering solution to generate the rendered questions and tests. Crucially for MathAssess, Includes MathML support for Internet Explorer+MathPlayer as well as for Mozilla Firefox.
..More Information about QTIEngine
MathAssess tools: Minibix
Minibix+ is an enhancement of Minibix with these new features:
- Mathematical capability
- Store both items and tests
- Better search and metadata editing
- Support organisation by taxonomy
- Support and advice for online testing
...More Information about Minbix
Moodle Plug-in
The Moodle plug-in allows the the QTI engine to run as a component in Moodle. Thereby allowing an lecturer to set a test and students take the test as part of a course in Moodle.
More information on installing and configuring the QTI engine.
J-Assess
JAssess has been used in its desktop implementation as developed for the earlier Aqurate project. This has been of particular importance in relation to writing of well-formed mathematical exemplars in QTI. As the project progressed this developed into studies of the whole feasibility of incorporating mathematical questions into QTI XML. The advantage of using JAssess to test the experimental XML which has been produced has been that the JAssess code itself could be modified by its author to accommodate the new ideas. In particular this made it possible to examine how far standard QTI XML was capable of supporting new directions, and to identify and study the extensions to QTI XML functionality which are required.
SnuggleTex, ASCIIMathML and interconversion of mathematical formats
There are a number of different formats for communicating and displaying mathematical information and it has become apparent that we will most likely not be able to settle on a single format to fulfil all of the aims of this project. Because of this, there is a requirement to be able to safely and reliably translate mathematics between the different forms that we adopt.
In general, this task is impossible as the language of mathematics is exceptionally complex and relies heavily on readers' understanding of the underlying contexts. For example, it is possible for the same concepts to be represented in multiple notations (e.g. differentiation using operator notation or Leibniz notation) and symbols and conventions are often reused for multiple purposes (e.g. e may be the exponential number or the identity in a group; a 2-dimensional vector may be denoted using the same notation as a binomial coefficient).
In order to make this problem manageable within the scope of this project, it is recommended that the type of mathematics we consider is restricted to a subset that satisfies the following conditions:
- Encompasses the type of mathematics we would expect up to an Educational Level 7 course on calculus
- Adopts a single common notation for input and output
- Can be reliably converted between different markup formats using a pre-defined set of conventions (e.g. assuming that 'e' is the exponential number, 'i' is the imaginary number).
It is suggested that following subset of mathematics can be safely supported:
- Common elementary functions, using any combination of latin or greek variable names
- Groupings, sums, differences, products, quotients and compositions of these
- Inverses, integer powers and roots of elementary functions
- Lists and sets
The project stakeholders must decide whether this is going to be sufficient. There is possibly scope in generalising things slightly but this increases the likelihood that conversions between certain formats will not be easy (if at all possible), making the resulting system brittle and potentially dangerous.
